Tradizione vuole che ad aprile il Carnevale della Matematica lo ospitiamo qui su MaddMaths!. Almeno, stando allo storico del calendario matematto, pare che le cose siano andate sempre così. Sarà che aprile è il mese della consapevolezza in matematica e statistica, ogni anno con un tema? Oppure, c’è stato qualche altro evento scatenante che ci ha appicciato addosso questo mese? Vabbè, lasciamo irrisolta la questione perché è il momento di dare il via al Carnevale della Matematica #177.
Non torniamo sulle ricorrenze di questo giorno, su chi è nato e chi è passato a miglior vita. Il 14 aprile è sempre lo stesso, come si diceva sopra, quindi vi rimandiamo a qualche altro nostro carnevale, come quello dello scorso anno a tema intelligenza artificiale.
Passiamo subito alle proprietà del numero di questo carnevale: il \(177\). È un numero dispari e difettivo, cioè minore della somma dei suoi divisori propri. È un numero semiprimo, poiché è la somma di due primi, \(177=59\times 3\), ed è palindromo in base \(11\), infatti \((177)_{11}=(151)\). È un numero omirpimes, cioè è un semiprimo non palindromo, le cui cifre scritte in ordine inverso danno luogo a un altro semiprimo, \(771=3\times 257\). Non sarà sfuggito a qualcuno che omirpimes altro non è che semiprimo, ma scritto al contrario. \(177\) è anche un numero poligonale, poiché lo si può disporre così da raffigurare un poligono regolare. A questo \(177\) non mancano certo nomi e appellativi; è (anche!) sia numero di Leyland che di Ulam. Vi sembra troppo? Tranquilli, in fin dei conti, è comunque un numero ideoneo.
Dopo tutte le proprietà del \(177\), apriamo pure il sipario sul Carnevale della Matematica #177. Nella Poesia Gaussiana (o dell’unicità della fattorizzazione) di Popinga, la strofa per questo carnevale è “il merlo, piccolino”. Dioniso Dionisi di Pitagora e dintorni ci regala la corrispondente cellula melodica:
Per ogni Carnevale della Matematica c’è un tema, con la libera licenza di interepretazione di chi vi partecipa. Per questo #177 abbiamo scelto: matematica inesauribile. Le chiavi di lettura possono essere moltiplici. Ma, partiamo da un pressuposto. La storia della matematica è davvero lunga, con un numero enorme di problemi e questioni, alcune delle quali ancora aperte. E, ogni epoca storica, con i suoi cambiamenti e stravolgimenti, ha alimentato la matematica e la sua comunità. Ad esempio, ora siamo nel periodo dell’Intelligenza Artificiale, e la ricerca matematica guarda eccome in quella direzione che è anche la direzione della società del futuro. In questo senso, è la stessa realtà a rendere inesauribile la matematica.
In questo discorso di matematica inesauribile si inseriscono problemi matematici che hanno avuto bisogno di molto tempo prima di trovare una soluzione. Viene subito in mente l’ultimo teorema di Fermat. In realtà, dovremmo dire ultima congettura di Fermat, poiché così è arrivata a noi, sebbene lo stesso Fermat sostenesse:
“Ho una meravigliosa dimostrazione di questo teorema, che non entra nel margine stretto della pagina [dell’Arithmetica di Diofanto].”
Questo problema ha tenuto impegnata la comunità matematica per oltre 350 anni. Infatti, è stato risolto solo nel 1994 dal matematico britannico Andrew Wiles, con la dimostrazione pubblicata nel 1995. Tuttavia, per arrivare alla soluzione Wiles ha speso gran parte del suo tempo di ricercatore, non condividendo quasi con nessuno i progressi della sua ricerca. Forse, in questo caso si innescano anche questioni personali, oltre che il desiderio di risolvere un problema.
Ci sono problemi per i quali non è arrivata una vera soluzione, ma si è scoperto che in base al contesto le risposte possono cambiare. È il caso del quinto postulato di Euclide, che (almeno in tempi moderni) scriviamo come:
“dati una retta \(r\) e un punto \(P\) non appartenente a essa, è possibile tracciare per \(P\) una e una sola retta parallela alla retta \(r\).“
Euclide è vissuto tra il III e il IV secolo a.C., eppure ci sono voluti migliaia di anni prima di capire che il quinto postulato non si potesse dimostrare. Tuttavia, questo lavoro ha portato alle geometrie non-euclidee, a partire dai lavori di Nikolaj Ivanovič Lobačevskij e János Bolyai.
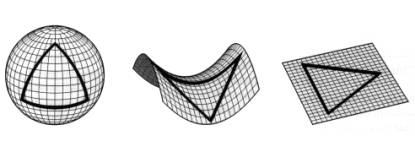
Da sinistra a destra, la rappresentazione di un triangolo in geometria sferica, iperbolica ed euclidea.
E, poi, ci sono problemi matematici ancora aperti. È il caso della congettura di Riemann, che tende fortemente ai 200 anni, essendo stata formulata da Bernhard Riemann nel 1859. Di tanto in tanto sembra esserci qualcuno che l’abbia risolta, eppure è ancora lì a sfidare la comunità. La sua soluzione, positiva o negativa che sia, avrebbe diverse ripercusioni, tra cui in crittografia. L’impegno verso questo problema è anche dettato dal mondo esterno alla comunità matematica e la sua evoluzione. Quindi, si alimenta sia dall’interno che dall’esterno. Ecco, proprio un bell’esempio di matematica inesauribile!
Passiamo ai contributi sul tema di questo carnevale.
“Il tema del Carnevale di aprile 2024, “Matematica inesauribile”, mi ha fatto immediatamente pensare ai Teoremi di Incompletezza di Gödel che penso forniscano una nozione precisa di inesauribilità, proprio perché in definitiva affermano che le teorie possono essere estese all’infinito con asserzioni di coerenza e che qualsiasi teoria può essere estesa al punto da produrre una teoria decisamente più forte.
In proposito ricordo un libro interessante, “Inexhaustibility – A Non-Exhaustive Treatment – Lecture Notes in Logic” dove Torkel Franzén dimostra proprio che la nostra conoscenza matematica è inesauribile.”
“La parola caos nelle antiche cosmologie indica il disordine, mentre nel campo della matematica e della fisica un sistema tende al caos quando le sue leggi di evoluzione comportano, dopo un certo intervallo di tempo, comportamenti del tutto imprevedibili e irregolari (e anche “inesauribili”, pensate al viaggio inesauribile all’interno di un insieme di Mandelbrot). Il libro che più mi ha spinto ad interessarmi del caos è di James Gleick, pubblicato a fine anni ’80 con il titolo: Caos – La nascita di una nuova scienza; se non lo avete ancora letto, questo è un classico da non perdere.
Si potrebbe citare il lavoro di Poincaré sul problema dei tre corpi che è alla base della teoria del caos deterministico e della conseguente teoria dei sistemi complessi. Ma potremmo studiare anche il moto di un pendolo doppio o più semplicemente il fumo di un fiammifero acceso, tutti studi non banali. Ricordo di aver assistito all’esposizione di una tesi sulla transizione da liquido a vapore dell’acqua all’ebollizione (molto bella e complessa) il cui titolo era: La scoperta dell’acqua calda. In questo post si parla dei lavori di Mitchell Feigenbaum che è riuscito a trovare l’inesauribile con una semplice calcolatrice scientifica.“
“Per me matematica inesauribile significa inesauribile caparbietà: a partire dalla mia storia personale e addentrandomi poi nella storia della matematica, trovo che per arrivare alla soluzione di un problema, alla dimostrazione di un teorema o a un risultato ambito, atteso, voluto, sia necessaria tanta determinazione, o forse, meglio ancora, caparbietà. Partendo dal classico Ultimo Teorema di Fermat e da Andrew Wiles, passando per Gigliola Staffilani, Sophie Germain e Michel Talagrand e chiudendo il percorso con Maryam Mirzakhani, raccontata da Alex Eskin, propongo una riflessione che coinvolge anche la didattica, cercando di stabilire quale sia la caratteristica necessaria per una buona riuscita in campo matematico.”
Di recente, matematica inesauribile l’abbiamo ritrovato anche al cinema. È da qualche giorno in sala il film “Il teorema di Margherita”, un film di Anna Novion che ha al centro una giovane matematica. La sua è una storia di passione per la matematica e di tanto lavoro intorno a questa disciplina. Tuttavia, è anche un racconto sulle difficoltà che (soprattutto) le ragazze incontrano in questo mondo, trovandosi costrette, in alcuni casi, a rinunciare. Sì, è anche una storia di rinuncia alla matematica, ma con un ritorno alla matematica. E, poi, è anche una storia d’amore. Tutto questo, e molto altro, lo trovate nel commento fatto per MaddMaths! da Anna Maria Cherubini nell’articolo Il teorema di Margherita – recensione di Anna Maria Cherubini.
La matematica è inesauribile anche perché ci sono idee che durano nel tempo, anzi maturano, e continuano a essere studiate e applicate, benché i progressi e (in alcuni casi) le rivoluzioni della società, come quella industriale o quella dell’intelligenza artificiale. È il caso delle equazioni di Eulero della fluidodinamica. Dopo secoli (sì, sono passati secoli!) ci sono ancora problemi aperti intorno a queste equazioni che non riguardano solo il fascino matematico della questione, ma anche l’eventuale impatto applicativo.
Ne ha parlato Marco Menale nel secondo episodio le equazioni della fluidodinamica della nuova serie, a cura della redazione di MaddMaths!, La Matematica è piena di Eulero!. Citando proprio l’articolo:
Dopo i contenuti sul tema di questo Carnevale, Matematica inesauribile, passiamo agli altri contributi. E come ogni Carnevale che si rispetti, ce ne sono proprio tanti, per tutti i gusti. Via pure con la sfilata:
Cominciamo con i Rudi Matematici. Prima dei contenuti per questo carnevale, hanno lasciato un’informazione di servizio: sono passati da un post alla settima a tre al mese. Un po’ dispiaciuti per questo piccolo taglio, godiamoci quanto hanno inviato:
Dr. Jekyll & Mr. Hyde sembrerebbe un giochino, dal titolo, ma invece è un lungo articolo (Paraphernalia Mathematica, li chiamiamo noi) scritto dal GC, che parla dei punti notevoli – anche se magari poco noti – dei triangoli. È possibile che la vostra opinione sui triangoli cambi faccia, dopo averlo letto, proprio come la faccia del Dr. Jekyll cambia quando si trasforma in Mr. Hyde.
Mezzi di trasporto forzati è il “post istituzionale”, ovvero il contenitore delle soluzioni ricevute al problema posto direttamente sulle pagine di “Le Scienze”. Ovviamente, si può aspettare a leggere le soluzioni e provare prima a risolvere il problema, anche se in questo caso specifico i tram prendono il posto dei dadi e le tasche dei pantaloni prendono il posto dei giocatori.
Buon compleanno, Sophie! è, con tutta evidenza, un “compleanno”. E, visto che il titolo fa gli auguri a Sophie, non ci vorrà poi tanto a capire che la protagonista è Sophie Germain. Il titolo originale del pezzo era “Dietro il bianco”, e l’abbiamo scritto nell’Aprile del 2017, sette anni fa.
Il numero di Marzo dell’e-zine è riuscito ad uscire ad Aprile, che è cosa che non tutte le riviste riescono a fare con nonchalance. Quello di Aprile farà del suo meglio per uscire ad Aprile, ma va a sapere… oh, comunque quello di marzo è il trecentoduesimo, e lo si può prendere da qui: RM302.
Dalle Notiziole di Maurizio Codogno arriva un bel carico per questo Carnevale. Come solito, li elenchiamo per rubrica:
“Trattasi di un post dedicato ad un rilevante problema nella teoria della probabilità, il cosiddetto paradosso di Bertrand, che risulta utile anche per mostrare l’ambiguità di alcune idee apparentemente intuitive spesso invocate a sproposito in ambito fisico.”
Dioniso Dionisi partecipa a questo carnevale con due contributi dal suo blog Pitagora e dintorni:
Il mistero della discesa infinta a Palermo Contiene qualche foto della presentazione palermitana de “Il mistero della discesa infinita”. Coinvolgere e incoraggiare studenti è una delle esperienze più gratificanti. E lo è stata anche questa con gli studenti del liceo musicale di Palermo.
Sul filo di lana arrivano i contributi del nostro Gianluigi Filippelli su DropSea (tanto sul filo di lana che li abbiamo inseriti con un certo ritardo… ce ne scusiamo con l’autore). Sentiamo dalla sua viva voce cosa ci propone.
Partirei dal tradizionale articolo post-pi day con la Breve storia del pi greco giunta quest’anno alla sua 12.ma puntata e che, come lo scorso anno, è leggermente tematica: Breve storia del pi gredo / Edizione algoritmica
Passo ora alle recensioni, che mi sbrigo abbastanza facilmente, con la serie Matematica della Gazzetta dello Sport:
Quest’ultimo è stato un libro di grande ispirazione perché ben due post sono stati a esso collegati. Il primo è quello in cui partendo dalla news del Turing Prize ad Avi Wigderson mi ha fatto finire con, guarda un po’, il pi greco! Il secondo, della serie dei Rompicapi di Alice (che poi è quello che ho appena pubblicato prima di mandarvi l’e-mail), si occupa del paradosso del compleanno – Un festa di compleanno
Un ultimo post ispirato alla serie curata da Maurizio Codogno fa parte della serie dei Paralipomeni di Alice: ne Il demone e la formica risolvo uno dei problemi proposti da Maurizio con lo sguardo del fisico (che è leggermente diverso).
Tra i post sparsi di varia natura (fuori da qualsiasi rubrica) abbiamo:
Il rapporto tra i fiumi e il cambiamento climatico in cui approfondisco il concetto matematico dell’entropia di ripartizione, usata per esaminare i dati relativi alla ricerca climatica raccontata nel post.
E infine dal Caffè del Cappellaio Matto il post di appoggio al video di Disney Comic&Science L’effetto fisarmonica dedicato ad alcuni particolari modelli matematici di evoluzione dell’universo.
Chiudiamo i contenuti di questo Carnevale della Matematica #177 con chi vi ospita. Eh sì, ci siamo proprio noi di MaddMaths!. Prima della lista di questo mese, che è veramente corposa, vi inviatiamo a iscrivervi alla nostra nuova (bellissima, ovviamente!) newsletter, almeno a quei pochi che ancora non l’hanno fatto. Bando alle ciance, e partiamo:
Formula di Eulero, Teorema di Eulero, Funzione di Eulero, Caratteristica di Eulero, Costante di Eulero, Numeri di Eulero, Metodo di Eulero, … L’elenco potrebbe continuare a lungo; basta scorrere le voci di wikipedia per farsi un’idea. In effetti, Eulero è stato uno dei matematici più prolifici della storia: ha scritto 886 pubblicazioni, tra libri e articoli. È una scommessa pressoché sicura che ogni matematico ha il suo “Teorema di Eulero'” o la sua “Formula di Eulero” preferita. La Matematica è piena di Eulero! è una serie che raccoglie le scelte di alcuni membri del comitato di redazione di MaddMaths!, ai quali abbiamo chiesto di presentare uno di questi argomenti ai nostri lettori e lettrici. Per i primi due episodi:
Immagina rider che sfrecciano per la città su biciclette ed e-bike, consegnando alimenti donati da attività locali alle mense sociali. Questo è il cuore di uno progetto formativo che sfida studenti e studentesse di Ingegneria Gestionale a sviluppare un piano logistico per la riduzione degli sprechi alimentari. A cura di Anna Livia Croella e Martina Gregori, ricercatrici dell’Università degli Studi Roma La Sapienza, che lo raccontano nell’articolo Ottimizzazione sostenibile per gli sprechi alimentari.
In occasione della Giornata Internazionale delle Donne in Matematica May12, mercoledì 8 maggio dalle 9.30 alle 13, presso l’Università degli Studi di Napoli Federico II, nel Complesso Universitario di M. S. Angelo a Napoli, si terrà l’evento UMI per la Festa delle Donne Matematiche 2024 a cura del Comitato Pari Opportunità dell’UMI e del Dipartimento di Matematica e Applicazioni “R. Caccioppoli”, con la collaborazione di MaddMaths!.
Il 13 marzo 2024 è stata inaugurata CUB3S, omaggio\(^3\) aperto e incompleto. La mostra prevede un allestimento fisico nello spazio espositivo PerArtEM presso l’IIS Via Roma 298 di Guidonia e uno virtuale accessibile anche tramite visore VR all’interno del sito web artsteps. Ce ne parla il docente responsabile del progetto Roberto Ianigro nell’articolo Inaugurata a Guidonia la mostra CUB3S.
È su Netflix la serie tv Il problema dei tre corpi, creata da David Benioff, D. B. Weiss and Alexander Woo, (i primi due sono stati i creatori di Game of Thrones) basata sull’ominimo romanzo di fantascienza dello scrittore cinese Liu Cixin. Senza nemmeno aver visto il trailer della serie, Roberto Natalini suggerisce alcuni punti di vista matematici che potrebbero tornare utili se non agli spettatori della serie, almeno ai lettori della trilogia da cui è tratto, nell’articolo Il problema dei tre corpi, romanzo matematico
Il premio Abel 2024 è andato aMichel Talagrand. Nell’articolo Michel Talagrand, premio Abel 2024: come matematizzare la complessità Adriano Barra ci racconta che questo premio è legato in modo molto stretto alla scuola romana di meccanica statistica e sistemi complessi, dagli studi e teorie sviluppati negli anni da Giorgio Parisi fino al contributo matematico di Francesco Guerra.
L’Operazione Cielo è un progetto ideato dall’associazione non-profit Il Cielo Itinerante fondata nel febbraio 2021 da Ersilia Vaudo, Alessia Mosca e Giovanna dell’Erba per avvicinare ragazze e ragazzi allo studio delle materie STEM, in particolare alla matematica, attraverso sei Summer Camp tra Napoli, Roma e Milano. L’idea è fare interagire i giovani con un nuovo approccio di insegnamento della matematica attraverso esperienze e attività che derivano dall’incontro de Il Cielo Itinerante con il movimento Youcubed , ideato nel 2013 da Jo Boaler e Cathy Williams, professoresse dell’Università di Standford. Scopriamo questo progetto insieme a Lorenzo Paderni e Vincenzo Mattera, studenti di Matematica della Federico II di Napoli nonché educatori che hanno preso parte ai Summer Camp, nell’articolo Operazione Cielo: portiamo il cielo dove non arriva.
Con il numero di Aprile de Le Scienze troverete in allegato (a 14,90 euro, il prezzo include la rivista) il diciannovesimo dei venticinque volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al teorema di Cauchy-Kovalevskaja ed è a cura di Sandra Lucente.
Le News di Stefano Pisani:
Problemi di matematica e come “disegnarli” Un team dell’Università di Ginevra, in collaborazione con l’Università CY Cergy di Parigi e l’Università della Borgogna ha analizzato i disegni realizzati da bambini e adulti durante la risoluzione di semplici problemi di matematica scoprendo che, a prescindere dall’età, le strategie di calcolo più efficaci sono associate a determinate tipologie di disegno.
Ecco i segreti per correre come campioni Nella corsa, è fondamentale lo scatto e la rapidità nei primi 50 metri e un rallentamento meno brusco in una gara di 400 metri. A rivelarlo è un nuovo modello matematico elaborato studiando i parametri fisici e psicologici dei campioni Matthew Hudson-Smith (400 m), Femke Bol (400 m), Jakob Ingebrigtsen (1500 m) e Gaia Sabbatini (1500 m).
La Lente Matematica di Marco Menale
Giocare con la Matematica Il 14 Marzo si celebra la “Giornata Internazionale della Matematica”. E il tema del 2024 è: Giocando con la Matematica.
Il modello di Gompertz per la crescita di popolazioni Il modello di Malthus e l’equazione logistica sono i più noti modelli di crescita di popolazione. Tuttavia, ce n’è un altro, forse meno noto, ma particolarmente usato in biologia: il modello di Gompertz.
Angolo Kos ed expected goals L’expected goals (xG) misura la probabilità di trasformare in goal un’occasione di gioco. È uno dei numeri più utilizzati nel calcio. Il suo calcolo passa per la scelta di alcuni parametri, come l’angolo Kos.
Sta per concludersi il Carnevale della Matematica #177, con il tema Matematica insuperabile. Di contenuti ne abbiamo avuti tanti, un po’ per tutti i gusti, dentro e fuori dal tema. Per sapere dove si terrà il prossimo Carnevale, e con quale tema, consultate il calendario matematto. Perché, come i problemi e le sfide della matematica, anche il carnevale della matematica è insuperabile!
This website uses cookies to improve your experience. We'll assume you're ok with this, but you can opt-out if you wish.AcceptRead More
Privacy & Cookies Policy
Privacy Overview
This website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience.
Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.
Trackback/Pingback