Pochi giorni fa sul sito di preprint ArXiv, il matematico Jineon Baek ha pubblicato un preprint in cui annuncia la soluzione di un problema matematico abbastanza inusuale: qual è l’area del più grande divano che può essere fatto passare per un corridoio di larghezza costante a forma di L? In attesa di sapere se questo risultato sarà confermato, Riccardo Moraschi ci racconta di cosa si tratta.
É capitato un po’ a tutti di dover acquistare un divano e le caratteristiche da tenere in considerazione sono molte: la forma, il materiale, il colore, gli accessori. Il matematico Leo Moser nel 1966 pensò che una caratteristica peculiare fosse la sua manovrabilità e da qui nacque il problema del divano. Qui su MaddMaths! ne abbiamo già parlato in due articoli [1 ] A. Sepe, “Il problema del divano”, sito Web MaddMaths!, (2013), link. [2 ] N. Ciccoli, “Quando un divano diventa un problema di matematica”, sito Web MaddMaths!, (2017), link. .
Per riassumere, consideriamo un corridoio di larghezza 1 con un angolo retto e vogliamo capire quale sia il divano più grande che possa essere spostato in questo corridoio. Un esempio di divano adatto è il quadrato di lato 1, la cui area è 1. Un altro divano interessante e non banale è il semicerchio di raggio 1, la cui area è \pi/2\approx 1.57.

Figura 1. Il quadrato
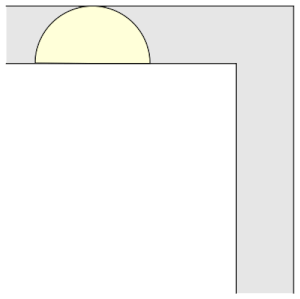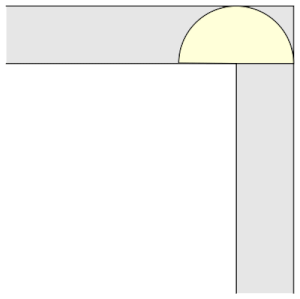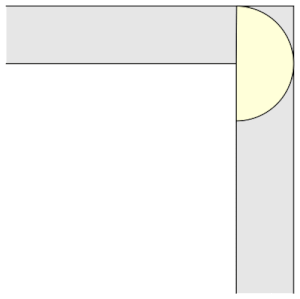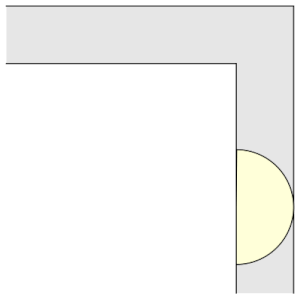
Figura 2. Il semicerchio
Osserviamo che il quadrato percorre l’angolo retto traslando mentre il semicerchio ruotando. L’idea di Hammersley nel 1968 fu quella di combinare questi due risultati così da ottenere il divano in figura che roto-traslando riesce a percorrere il corridoio. Per ottenere una figura che permetta ciò, dividiamo il semicerchio in due parti, allontiamole, inseriamo un rettangolo nel mezzo e rimuoviamo un piccolo semicerchio affinché riesca a ruotare. L’area di questo divano è 2.2074.

Figura 3a. Il divano di Hammersley
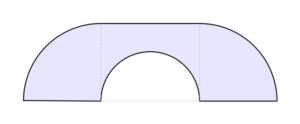
Figura 3b. Il divano di Hammersley
Hammersley congetturò che questo fosse il divano ottimale (ossia quello che massimizzasse l’area). La congettura si rivelò falsa quando nel 1992 Gerver propose un nuovo divano che avesse area maggiore di quello di Hammersley. Il divano di Gerver può sembrare molto simile a quello di Hammersley ma in realtà risulta essere molto complesso: è formato da 3 linee dritte e 15 segmenti curvilinei, ognuno descritto dalla propria formula. Questo divano ha un’area maggiore di tutti i precedenti: 2.2195. La differenza sostanziale tra i due è che quello di Gerver non è il risultato di una costruzione “manuale” bensì di determinate equazioni differenziali. Questo però non risolve il nostro problema perché, seppur geniali, le idee di Gerver non permettono di dimostrare che il divano da lui trovato sia effettivamente quello ottimale. La congettura è rimasta aperta per molto tempo e numerosi matematici si sono interessati a questo problema.
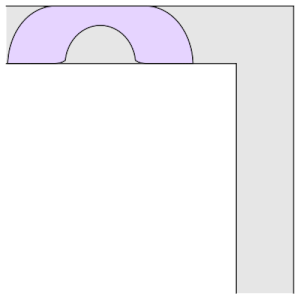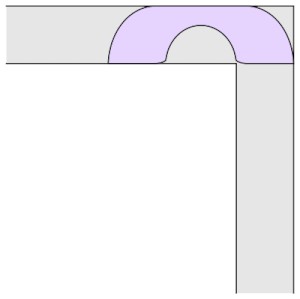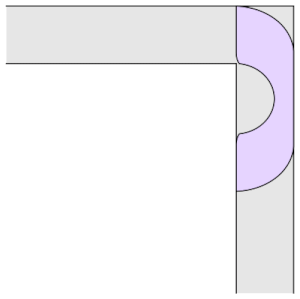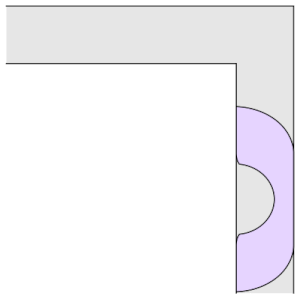
Figura 4a. Divano di Genver

Figura 4b. Divano di Genver
Nel 2024 Deng [3 ] Z. Deng, “Solving Moving Sofa Problem Using Calculus of Variations”, (2024), arXiv. ha affrontato il problema utilizzando tecniche di Calcolo delle Variazioni. In particolare è riuscito ad esprimere l’area del divano come funzione delle bordo del divano definendo così una funzione che “calcolasse l’area”. Passando poi all’equazioni di Eulero-Lagrange associate a questo problema, ha dimostrato che il divano di Genver le soddisfa. Questo garantisce che il divano di Gerver sia un punto critico per la funzione d’area ma non sappiamo ancora se sia un massimo globale. Grazie però a un recente articolo di Baek [4 ] J. Baek, “Optimality of Gerver’s Sofa”, (2024), arXiv., pubblicato come preprint il 29 novembre scorso, ora possiamo forse finalmente affermare che il divano di Genver è la risposta corretta alla nostra domanda. Avevamo diversi motivi per presupporlo:
- Genver ha mostrato che dato un divano ottimale, questo deve soddisfare la “condition” e il suo divano la soddisfa
- É punto critico per il funzionale d’area.
L’idea della dimostrazione di Baek è la seguente: consideriamo un insieme S che soddisfa una condizione detta “injectivity condition”. Ingrassiamo questo insieme in modo che assomigli al divano di Genver. In questo modo otteniamo un nuovo divano di area Q(S) che sarà maggiore o uguale a quella di S. Esprimendo in modo intelligente l’espressione di Q(S) e sfruttandone le proprietà di concavità, si dimostra che ammette il suo massimo se S è il divano di Genver. Se il risulato di Baek sarà confermato, ricordiamo che stiamo parlando di un preprint, il problema del divano sarebbe allora definitvamente risolto.
Crediti: le GIF sono state prese da [5 ] Dan Romik’s home page, link. . L’immagine di copertina è realizzata con Canva.
Note e riferimenti
| ⇧1 | A. Sepe, “Il problema del divano”, sito Web MaddMaths!, (2013), link. |
|---|---|
| ⇧2 | N. Ciccoli, “Quando un divano diventa un problema di matematica”, sito Web MaddMaths!, (2017), link. |
| ⇧3 | Z. Deng, “Solving Moving Sofa Problem Using Calculus of Variations”, (2024), arXiv. |
| ⇧4 | J. Baek, “Optimality of Gerver’s Sofa”, (2024), arXiv. |
| ⇧5 | Dan Romik’s home page, link. |




















Negli anni 90 ci ha lavorato anche Maurizio Saroldi all’ Università di Firenze. Forse il suo lavoro è rimasto oscuro perché ricordo di aver versato inavvertitamente del caffè sulle immagini della sua tesi di laurea.
Spero davvero che la dimostrazione di Baek sia valida e che questo problema che mi ha fatto passare notti insonni sia finalmente risolto. La mia tesi di laurea del 1993 riguardava proprio il problema del divano, ma ero riuscito solo a dimostrare l’esistenza di quello di area massima con una nuova tecnica ma non a determinarne la forma.
Complimenti a Baek e, ovviamente, a Genver