Recentemente il matematico canadese Simon Plouffe ha ottenuto la piú lunga sequenza di numeri primi ottenuti mediante una formula semplice. Cosa ha a che fare questo tipo di risultato con la ricerca sui in teoria dei numeri? E come funzionano queste formule? A queste e altre curiosità risponde con la consueta chiarezza il nostro Alessandro Zaccagnini.
Periodicamente mi capita di imbattermi in formule che producono numeri primi: si tratta di ricette piú o meno complicate e interessanti, naturali o artificiali; insomma, c’è un po’ di tutto, perché la parola “formula” è sufficientemente vaga da coprire un ampio spettro di significati. Personalmente trovo curiosa l’enfasi intorno a questo argomento, come se formule di questo tipo fossero la pietra filosofale con la quale trasformare, mediante un astruso procedimento alchemico, un volgare e comune numero intero in un prezioso e raro numero primo. In effetti, nelle mie ricerche sui numeri primi non hanno mai avuto la minima rilevanza; però alcune di queste rappresentano un ottimo strumento didattico per mostrare quello che sono, e anche quello che non sono, i numeri primi e per questo motivo ne includo sempre qualcuna nei miei corsi.
Questo breve articolo è dunque dedicato a demistificare l’argomento, trattando tre o quattro casi interessanti. Lo spunto è dato da un recente articolo di Simon Plouffe, un matematico canadese coautore dell’interessantissima “Encyclopedia of Integer Sequences” del 1995. La versione moderna e aggiornata si trova all’indirizzo http://oeis.org/ ed è una vera miniera di informazioni.
Per cominciare, distinguiamo tra formule che danno tutti i numeri primi in ordine e formule che danno solo numeri primi per ogni valore della variabile intera. Ho parlato per esteso delle formule del primo tipo in [1 ]A. Zaccagnini, Macchine che producono numeri primi, Matematica, Cultura e Società 1 (2016), no. 1, 5–19, dove ho descritto la macchina di Conway, la formula di Gandhi per l’ennesimo numero primo \(p_n\) e una formula per \(\pi(n)\), il numero dei numeri primi che non superano \(n\), basata sul Teorema di Wilson. Per questo motivo, qui mi concentro sulle formule del secondo tipo.
La piú antica di tutte sembra essere la formula di Eulero \(f(n) = n^2 + n + 41\), che però non risponde in pieno alla nostra richiesta, dato che \(f(41)\) non è un numero primo. In effetti, è facile vedere che \(f(41 n)\) è divisibile per \(41\) qualunque sia \(n\) intero. Allora, qual è l’interesse di questa formula? Intanto, \(f(0)\), \(f(1)\), \(f(2)\), …, \(f(39)\) sono tutti numeri primi e, anche se poi \(f(40)\) ed \(f(41)\) sono composti, questa funzione continua ad assumere numerosissimi valori primi: 581 fra i primi 1000 interi.
È possibile che un polinomio a coefficienti interi e non costante assuma solo valori primi, migliorando la performance del polinomio di Eulero? Non è troppo difficile vedere che la risposta è no: per esempio, se \(f(0) = p\) allora \(f(n p)\) è divisibile per \(p\) qualunque sia l’intero \(n\), ed è primo solo se \(f(n p) = \pm p\). Per ipotesi il polinomio \(f\) non è costante e ciascuna di queste due equazioni ha un numero finito di soluzioni.
Al proposito è molto interessante osservare quali sono le conseguenze della variante quantitativa del crivello di Eratostene, ottenuta con ricerche di molti matematici nel corso di tutto il XX secolo: la “maggioranza” dei valori \(f(1)\), \(f(2)\), \(f(3)\), …, \(f(n)\) è composta; piú precisamente, la percentuale dei numeri primi fra i valori elencati sopra tende a \(0\) quando \(n \to +\infty\). Infatti, il buon vecchio crivello può essere usato non solo per trovare numeri primi, ma anche per trovare valori primi tra quelli assunti da un polinomio a coefficienti interi. Invece di scrivere in una tabella i numeri \(1\), …, \(n\), si scrivono i valori \(f(1)\), …, \(f(n)\) e poi si eliminano i multipli di \(2\), di \(3\), etc. I polinomi hanno la simpatica proprietà di essere funzioni periodiche quando calcolate modulo un qualunque intero fissato (in particolare un numero primo, come abbiamo osservato sopra) e quindi, mutatis mutandis, quello che funziona per il crivello standard, cioè per il polinomio \(f(n) = n\), funziona anche piú in generale.
Una formula che invece rispetta in pieno la richiesta di fornire un numero primo diverso per ogni valore della variabile intera \(n\) è stata scoperta nel 1947 dal matematico W. H. Mills: esiste un numero reale \(A > 1\) tale che \(\lfloor A^{3^n} \rfloor\) è un numero primo per ogni \(n\) intero positivo, dove \(\lfloor x \rfloor\) indica il massimo numero intero che non supera \(x\). È stato dimostrato che \(A \approx 1.30637788 \dots\). Il gioco sembra fatto, ma in realtà per calcolare i numeri primi è necessario conoscere le infinite cifre decimali del numero \(A\), e allora tanto vale conoscere le infinite cifre decimali del numero \(0.2357111317192329\dots\) ottenuto scrivendo i numeri primi uno dopo l’altro. In entrambi i casi, abbiamo bisogno di una quantità infinita di informazione per calcolare quello che vogliamo, mentre, in un certo senso, lo spirito di una formula è di avere “pochi” parametri, come il polinomio di Eulero, che catturino almeno in parte l’infinita complessità dei numeri primi.
Inoltre, analizzando in dettaglio la dimostrazione di Mills, che sta tutta in una pagina, si vede subito che le proprietà “aritmetiche” dei numeri primi, per intenderci quelle legate alla divisibilità, non hanno alcun ruolo, ma serve solo il fatto che ogni intervallo della forma \(\bigl( N^3, (N + 1)^3 – 1 \bigr)\) contiene un numero primo, se \(N\) è sufficientemente grande; si tratta di una conseguenza di un importante risultato dimostrato poco prima dal matematico inglese A. E. Ingham. Incidentalmente, questo spiega perché compare il numero \(3\) nella formula di Mills.
Quindi, in realtà, esiste un numero \(A\) opportuno per ogni successione data che soddisfi questa ipotesi! In parole povere, come dicevamo la chiave della dimostrazione della formula di Mills sta nel fatto che c’è sempre un numero primo tra due cubi perfetti consecutivi. Ma lo stesso vale anche per moltissime altre successioni, come per esempio quelle dei quadrati perfetti: sapete dimostrare che c’è almeno un quadrato perfetto fra due cubi perfetti consecutivi? Per esempio fra \(10^3 = 1000\) ed \(11^3 = 1331\) ci sono \(32^2 = 1024\), \(33^2 = 1089\), …, \(36^2 = 1296\). Quindi, ripetendo parola per parola la dimostrazione di Mills in quest’altro caso, scopriamo che esiste un numero reale \(B > 1\) tale che \(\lfloor B^{3^n} \rfloor\) è un quadrato perfetto per ogni \(n\) intero positivo. Da questa prospettiva, il Teorema di Mills appare molto meno interessante di quanto potesse sembrare a prima vista.
In ogni caso, il guaio di questa e simili formule è che i valori crescono molto in fretta e quindi “mancano” la stragrande maggioranza dei numeri primi. Riassumendo: vogliamo una formula che sia la piú semplice possibile, non troppo artificiale e vogliamo anche che i suoi valori non crescano troppo rapidamente. Stiamo forse chiedendo troppo?
Qualche giorno fa il matematico canadese Simon Plouffe ha pubblicato l’articolo [2 ]S. Plouffe, A set of formulas for primes, Arxiv preprint 1901.01849, 2019, dichiaratamente empirico, nel quale stabilisce il nuovo incredibile record per la piú lunga sequenza di numeri primi ottenuti mediante una formula semplice e con crescita moderata. La formula in questione è una formula “ricorrente” dove \(a_{n + 1} = a_n^{\alpha}\), che viene innescata da un opportuno valore di \(a_0\). Qui ci sono due parametri a disposizione, e cioè l’esponente \(\alpha > 1\) ed il valore iniziale \(a_0\). Plouffe ha fatto alcuni esperimenti numerici con \(\alpha = \frac32\), \(\frac54\), \(\frac{11}{10}\) e \(\frac{101}{100}\).
Sperimentalmente, con i primi valori di \(\alpha\) è possibile scegliere \(a_0\) relativamente piccolo, ma le sequenze di primi ottenute in questo modo non sono molto lunghe. Nel caso in cui \(\alpha = \frac{101}{100}\), Plouffe ha scoperto che è possibile scegliere \(a_0\) in modo che le parti intere dei valori \(a_1\), \(a_2\), …, \(a_{50}\) siano tutti numeri primi, e questo rappresenta appunto il nuovo record. Nell’articolo si dice chiaramente che questo risultato è il frutto di ricerche fatte provando valori diversi di \(\alpha\) ed \(a_0\), e al momento non c’è un risultato teorico, come il Teorema di Mills, che garantisca l’esistenza di valori che danno un numero arbitrariamente grande di numeri primi.
Per concludere, qual è la piú semplice formula per produrre 50 o 100 primi consecutivi? Paradossalmente, è un polinomio di primo grado! C’è un risultato veramente straordinario dimostrato da Ben Green e Terence Tao nel 2008 [3 ]B. Green & T. Tao, The primes contain arbitrarily long arithmetic progressions, Ann. Math. 167 (2008), no. 2, 481–547 (pubblicato non a caso su Annals of Mathematics, forse la piú prestigiosa rivista di matematica al mondo) secondo il quale i numeri primi contengono progressioni aritmetiche arbitrariamente lunghe. In parole diverse, esiste un polinomio di primo grado i cui primi 50 o 100 o 1000 valori sono tutti numeri primi. Se ci accontentiamo di 6 valori consecutivi, possiamo prendere \(f(n) = 30 n + 7\), che è primo per \(n = 0\), …, \(5\) (ed anche per \(n = -1\), …, \(-4\)). Purtroppo, però il Teorema di Green & Tao è un risultato di pura esistenza, come si dice: sappiamo che, qualunque sia \(k\), esiste un polinomio di primo grado \(f(n) = an + b\) che assume un valore primo per \(n = 1\), \(2\), …, \(k\); cioè, \(a + b\), \(2 a + b\), \(3 a + b\), …, \(ka + b\) sono tutti numeri primi. Il guaio è che allo stato attuale delle conoscenze non sappiamo calcolare due valori ammissibili per i coefficienti \(a\) e \(b\), dato \(k\): l’unica cosa di cui siamo sicuri è che si tratta di coefficienti giganteschi, di fatto inaccessibili al calcolo, se \(k\) è grande.
Per approfondire la questione delle formule che producono numeri primi può essere utile consultare l’articolo originale di Simon Plouffe citato sopra, il Capitolo 3 del bel libro di Paulo Ribenboim [4 ]P. Ribenboim, The New Book of Prime Numbers Records, Springer, New York, 1996. , oppure il mio recente articolo [1 ].
Alessandro Zaccagnini
Note e riferimenti
| ⇧1 | A. Zaccagnini, Macchine che producono numeri primi, Matematica, Cultura e Società 1 (2016), no. 1, 5–19 |
|---|---|
| ⇧2 | S. Plouffe, A set of formulas for primes, Arxiv preprint 1901.01849, 2019 |
| ⇧3 | B. Green & T. Tao, The primes contain arbitrarily long arithmetic progressions, Ann. Math. 167 (2008), no. 2, 481–547 |
| ⇧4 | P. Ribenboim, The New Book of Prime Numbers Records, Springer, New York, 1996. |

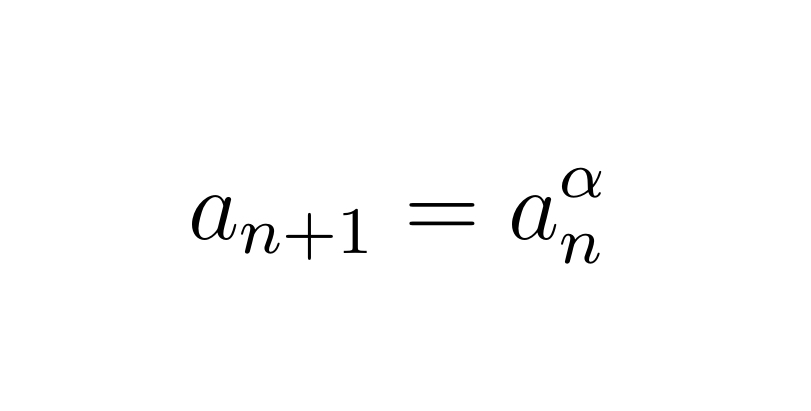




















Buongiorno. Più che un commento una domanda.
Oltre a quella di Eulero sono state rese note altre formule polinomiali che iniziano con i diversi numeri primi ? Mi Consta che la formula di Eulero “funziona” anche sostituendo a 41 i numeri 5,11 e 17.
Ho letto anche della formula 2x*x+29 attribuita a Legrenge.
Io mi sono divertito a “crearne” delle altre di varie “lunghezze” e vorrei avere un termine di paragone….
Grazie per l’attenzione
Settantenne in pensione Vittorio Ornago