Uno spinoff de “La Matematica Umida dell’Evoluzione”

THE LAST WOMAN

di Mary Shelley

VOL. I

____________________1____________________

Al lettore.

Benvenuto nel primo volume di un progetto a cui tengo molto, che mi rappresenta come madre, moglie e donna.
Il mio nome è Mary Shelley, moglie del fu Percy Bysshe Shelley, celebre e arcinoto poeta. Sono nata nell’anno del Signore 1797 e sono anch’io una scrittrice.
L’editoria londinese mi ha conosciuto principalmente come curatrice delle poesie di mio marito, tu lettore, invece, probabilmente avrai sfogliato il mio romanzo più famoso, Frankenstein, o il moderno Prometeo; più famoso, certo, ma non il più riuscito immaginando uno stile che sappia armonizzare fantasia e scienza.
Dopo la morte di mio marito, ormai più di vent’anni fa, in un periodo di profondo sconforto, mi dedicai interamente alla carriera di scrittrice, così da poter mantenere mio figlio, dedicai tempo a tentativi letterari che nel 1826 mi portarono alla pubblicazione di The Last Man, una storia con tinte dell’Apocalisse di Giovanni, sulla fine dell’Umanità a causa della Peste.
Ottenni le critiche più feroci della mia vita, venni derisa sul piano intellettuale e personale, “il prodotto di un’immaginazione malata e di un gusto assolutamente corrotto” scrissero…crollai nel profondo pozzo della depressione; The Wasp annunciò la mia opera direttamente e crudelmente con il titolo “The Last Woman”…

Oggi, 7 novembre 1850, rispondo a quelle critiche presentando questa serie di volumi di enigmi, giochi, storie, ambientati in un tempo futuro al nostro, una collezione prodotta dall’“immaginazione malata” e dal mio “gusto assolutamente corrotto”.
Lettore, non stupirti se questo lavoro si chiamerà proprio “The Last Woman”.

Vai al 2.

____________________2____________________

Introduzione.

Da tempo intrattengo un fitto rapporto epistolare con un naturalista inglese, da quando, nel 1836, tornò da un viaggio intorno al mondo. Mi racconta di avere in mente una teoria, di voler pubblicare una grande opera ma con ancora molti punti da sistemare. Una è l’idea che più mi ha ispirato, dalla quale far prendere il volo alla fantasia; ve la presento romanzando alcune delle lettere…

“Il 17 settembre del 1835 una piccola barca a remi si avvicinò alle coste dell’isola di San Cristòbal. A bordo della barca, il brigantino Beagle, c’era il naturalista di bordo, Charles Robert Darwin.
Il giovane approfittò di questo soggiorno di alcune settimane per dedicarsi alla raccolta di campioni di varie specie. Tra questi c’era un discreto numero di uccelli, e Darwin raccolse e conservò trentuno esemplari di fringuelli.
Questi uccelli presentano una sorprendente varietà: sulle isole delle Galapagos si può incontrare una quindicina di specie, ognuna caratteristica di un’isola. Tra specie e specie poco cambia a livello di colori, mentre ci sono differenze nella forma del becco: ce ne sono di sottili e adatti per catturare piccoli insetti e di robusti per rompere semi, ci sono becchi specializzati nel dedicarsi ai frutti e altri che danno il loro meglio con le foglie. Le variazioni di questi animali, tra un’isola e l’altra, sono sorprendenti.
Nonostante questo, le evidenti somiglianze nella morfologia generale sono la testimonianza di un fatto: tutti questi animali hanno un unico progenitore comune.

Darwin, una volta tornato a casa, cominciò a dedicare molto tempo a ragionare su quanto aveva osservato in giro per il mondo e i suoi fringuelli ebbero un peso importante nel fargli teorizzare alcuni meccanismi della selezione naturale. Tra questi c’erano la comparsa di nuove specie a partire da un antenato comune”.
Immortalò questo pensiero in un’immagine:

Ogni vivente deriva da un antenato comune unico, un LUCA (Last Universal Common Ancestor) che dopo molti eventi di speciazione ha generato la varietà che si ritrova in natura. Allora sarebbe giusto cominciare a catalogare ogni specie vivente tenendo conto dei rapporti “genealogici” che ha con ogni altra, una disciplina che potremmo chiamare “cladistica” (dal greco ramo, dell’albero del disegno sopra).
Ho pensato ad un gioco sulla parentela universale di tutti gli esseri viventi, vai al 3.

____________________3____________________

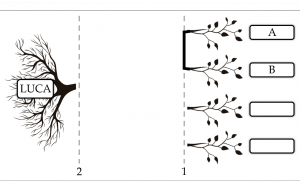
LUCA.
“Ricostruisci un albero cladistico a partire dalle distanze fra i vari organismi, per svelare i rapporti di parentela che intercorrono fra loro.”

Regole ed esempio guidato

4 organismi

Lo scopo del gioco è disegnare i rami dell’albero sotto sfruttando le informazioni contenute nella tabella sopra.
L’albero ha come foglie un certo numero di organismi (nell’esempio A, B, C, D, come indicati in tabella) e come radice LUCA, ultimo antenato comune universale, primo organismo dal quale tutti gli altri si sono evoluti.

La tabella si chiama matrice delle distanze: incrociando la colonna A e la riga B nell’esempio si ottiene 3, distanza fra gli organismi A e B, ovvero il tempo trascorso dall’evento di speciazione che da un antenato comune ha generato le due specie differenti. In altre parole, più due organismi hanno un valore di distanza grande, più è lontano nel tempo il loro antenato comune.

Ad ogni foglia dovrà corrispondere uno fra i quattro organismi della tabella; vediamo attivamente come fare:

Il numero più basso è 1, distanza fra B e C;
possiamo quindi collegare fra loro le due foglie e cancellare riga e colonna corrispondenti a B e C

Il minimo fra i valori rimasti è 2 ed è la distanza fra le foglie C e D. Poiché B e C formano un unico blocco ormai, in realtà è la distanza fra D e la coppia (B, C). Ragionando come prima

L’ultimo passaggio è come i precedenti. Il minimo, 3, è la distanza fra A e la tripletta (B, C, D) quindi l’albero finale ha la forma

A volte è possibile riordinare le foglie, in questo caso ottenendo

Se vuoi vedere un altro esempio, vai al 4.
Per proseguire al vero gioco, vai al 5.

____________________4____________________

4 organismi

In questo esempio l’albero finale è più piccolo perché nella tabella la distanza massima è solo 2.
Il minimo, 1, è raggiunto sia con la distanza fra A e B, sia fra C e D. Scegliamo A e B (la scelta è irrilevante), cancelliamo riga e colonna corrispondenti e cominciamo a completare l’albero

Il minimo è nuovamente 1, distanza fra C e D, quindi faccio il passo successivo, aiutato dai numeri presenti in basso sotto l’albero.

L’ultimo passaggio è il più semplice. 2 è la distanza fra la coppia (A, B) e la coppia (C, D), quindi posso completare l’albero, che in questo caso è già ordinato

Per proseguire al vero gioco, vai al 5.

____________________5____________________

9 organismi

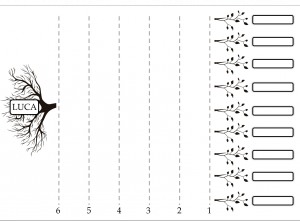
Quando hai risolto il gioco (e non prima!) va al 6.

____________________6____________________

Se vuoi entrare nel dettaglio per capire cosa si cela dietro al gioco, vai al 7.
Altrimenti vai all’8.

____________________7____________________

LUCA è un gioco che si basa su un algoritmo chiamato UPGMA, in grado di ricostruire alberi a partire da una matrice di distanze e utilizzabile per questo in vere ricostruzioni di alberi di parentela.
L’algoritmo ha limitazioni su due fronti:

L’albero non deve essere un albero qualunque.

UPGMA si applica esclusivamente ad alberi definiti ultrametrici, ossia con questa proprietà:
“Le distanze fra due foglie qualunque e il loro progenitore comune sono uguali”.
Per far funzionare il gioco si cerca il valore minimo nella matrice delle distanze e si interpretano le due foglie corrispondenti come fratelli, collegandole direttamente fra loro. Tale assunto è valido solamente con alberi ultrametrici.

Questo è un albero ultrametrico.
Le due foglie A e B distano entrambe 1 dal loro progenitore comune, indicato con “i”. Il progenitore comune fra A e C (o fra B e C) è “k” e dista 2 da entrambi. Il valore minimo nella matrice delle distanze sarà 1, distanza tra i due fratelli A e B.

Questo secondo albero non è ultrametrico, perché ad esempio “i”, progenitore di A e B, dista 1 da A e 4 da B. Calcolando la matrice delle distanze si ottiene

Il minimo, 4, è la distanza fra A e C, NON fratelli, quindi applicando l’UPGMA si arriverebbe ad un risultato errato.

È proprio la matrice delle distanze a mettere in luce il secondo problema.

Cosa rappresenta in dettaglio la distanza, e come calcolarla?

Non è semplice dare una risposta. Cosa rappresenta? Cosa si intende ad esempio per la distanza fra l’uomo e la scimmia è 2?
Le foglie rappresentano organismi viventi, e la distanza indica il tempo passato dagli eventi di speciazione che li hanno divisi. Ad esempio, se ammettiamo che 4 milioni di anni fa comparvero i primi ominidi creando il punto di separazione dalla linea che ha condotto alle scimmie africane antropomorfe, nostri parenti più prossimi, per entrambi, noi e le scimmie, il ramo dell’albero che ci unisce al progenitore comune sarebbe lungo 4 milioni di anni

Purtroppo non possediamo macchine che ci consentano di tornare indietro di 4 milioni di anni per osservare l’evento, e abbiamo bisogno di altri metodi per ricostruire l’albero, ma ne parleremo nel prossimo volume di The Last Woman.
Come ricompensa per essere arrivato in fondo a questo paragrafo, raccogli un Seme dell’Albero della Vita e vai all’8.

____________________8____________________

Il gioco che hai appena completato funziona anche da indice per i primi tre volumi di The Last Woman. Seguendo le indicazioni dei paragrafi potrai leggere enigmi e giochi a tema “biologico”. Li riporto qui per semplicità.
Buon viaggio!

Batteri, cercali nel Volume III;
Archaea, cercali nel Volume III;
Sanguisughe, vai al 12;
Polpi, cercali nel Volume II;
Coleotteri, cercali nel Volume II;
Rane, vai al 9;
Uomini, cercali nel Volume III;
Palme, cercali nel Volume II;
Muschi, cercali nel Volume II.

____________________9____________________

Tempo fa mi capitò di assistere ad una curiosa danza di corteggiamento fra rane. Mi trovavo presso lo stagno vicino casa, osservavo giocare mio figlio e guardavo quei curiosi anfibi saltellare e rincorrersi. Vorrei raccontarvi la scena senza farlo direttamente, quindi ho preparato un enigma.

Le quattro rane (che chiamiamo per semplicità A, B, C, D) occupano gli angoli di un quadrato di 1 metro di lato; A e C sono maschi, B e D femmine. Contemporaneamente A comincia a camminare direttamente verso B, B verso a C, C verso D, D verso A. Tutte e quattro si muovono alla stessa velocità, costante.

Quale figura formeranno le traiettorie delle quattro?

Quando pensi di saper rispondere, vai al 10.

____________________10___________________

Le quattro rane descriveranno 4 spirali che si incontrano al centro del quadrato, ma non spirali qualsiasi, 4 spirali logaritmiche.

Se non conosci le molte proprietà delle spirali logaritmiche, ti consiglio di aspettare il Volume IV di The Last Woman e di seguire gli indizi del nautilus.
(Il Volume IV è quello che J.M. Smith legge durante il suo viaggio, e lo puoi già trovare nel passato numero di La Matematica Umida dell’Evoluzione, qui. N.d.A.)
A qualsiasi istante dato, le quattro rane individuano i vertici di un quadrato che si restringe e ruota man mano che gli anfibi si avvicinano fra loro, generando la spirale.

La successiva domanda che ti pongo è:
Quanto deve camminare ogni rana prima dell’incontro con le altre? Il problema può essere risolto senza calcoli.

Quando sai rispondere o vuoi controllare le soluzioni, vai all’11.

____________________11____________________

Come detto, le rane in ogni istante individuano i vertici di un quadrato che si restringe ruotando.
Il percorso di ogni inseguitore sarà perciò sempre perpendicolare a quello dell’inseguito.

Questo dice che, mentre A, per esempio, si avvicina a B, non vi è nessuna componente del moto di B che lo avvicini o allontani da A.
Di conseguenza A raggiungerà B nello stesso tempo che occorrerebbe se B rimanesse fermo: la lunghezza di ogni braccio di spirale è la stessa del lato del quadrato, 1 metro.

Se vuoi leggere altri enigmi torna all’8; altrimenti vai al 15.

____________________12____________________

Tempo fa mi capitò di avere un momento di panico. Mi trovavo presso lo stagno vicino casa, osservavo giocare mio figlio. Non ricordo il motivo ma distolsi lo sguardo per qualche minuto. La disattenzione mi giocò un brutto scherzo… mio figlio era scivolato in acqua e rischiava di annegare!
Fortunatamente, a parte lo spavento non ci furono conseguenze, perché mi bastò entrare nell’acqua alta fino al ginocchio e portar fuori il piccolo spaventato. La sera tornando a casa mi accorsi di una macchia nera sulla caviglia: una sanguisuga!
Non avevo certo bisogno di un salasso, così la strappai via…
Salasso, pratica medievale! Conosco un indovinello medievale, di un tale Leonardo Pisano:

“Un uomo mise una coppia di conigli in un luogo circondato su tutti i lati da un muro. Quante coppie di conigli verranno generate in un anno a partire da quella coppia, se si suppone che ogni mese ogni coppia generi una nuova coppia che diviene fertile a partire dal mese successivo?”

Quando pensi di saper rispondere, vai al 13.

____________________13____________________

Leonardo Pisano è forse più noto come il Fibonacci, e questo indovinello dà luogo alla sequenza numerica che prende il suo nome.
Diciamo che una coppia è matura se può generare figli, immatura in caso contrario.
All’inizio abbiamo una coppia matura;
Al mese 1 questa coppia genera una coppia immatura, e così abbiamo una coppia matura e una immatura: 2 in tutto;
Si prosegue così:

Ogni termine è la somma dei due precedenti, molto semplicemente. Dopo un anno, avremo 377 coppie.
(Di questa famosa sequenza e delle sue proprietà in ottica naturale se ne è abbondantemente parlato in La Matematica Umida dell’Evoluzione 2, qui, N.d.A.).

Che sequenza si ottiene invece con quest’altra storia?

“Un uomo mise una coppia di piccoli conigli in un luogo circondato su tutti i lati da un muro. Quante coppie di conigli verranno generate in un anno a partire da quella coppia, se si suppone che ogni mese ogni coppia piccola diventi una coppia giovane, ogni coppia giovane generi una coppia piccola e diventi una coppia adulta, ogni coppia adulta generi due coppie piccole?”

Quando sai rispondere, vai al 14.

____________________14____________________

La sequenza che si ottiene è:

1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, …

Ogni numero è la somma degli ultimi tre, è la sequenza di Tribonacci!

Se vuoi leggere altri enigmi torna all’8.
Altrimenti vai al 15.

____________________15___________________

Grazie per aver supportato questo progetto, al prossimo numero!
Mary

Bibliografia

Enigmi e Giochi Matematici – Martin Gardner
A cosa pensava Darwin? Piccole storie di grandi naturalisti – Alfonso Lucifredi
L’ultimo uomo – The Last Man – Mary Shelley