Davide Palmigiani ci aiuta a scoprire i misteri dei soldati di Conway.

Immaginiamo un quadrettato infinito, diviso in due da una linea orizzontale che si estende in ogni direzione. Sopra la riga, tutte le celle sono vuote, sotto invece c’è un numero arbitrario di celle piene, i soldati. Così:

Su questo quadrettato facciamo un gioco, un solitario. Una mossa consiste nel far saltare un soldato sorpassandone un altro e occupando uno spazio libero, come per la dama, ma solo in orizzontale o verticale.

Da così

a così

o da così

a così

​ Lo scopo del gioco è piazzare un soldato il più lontano possibile dalla riga orizzontale. Quanto in alto riesci a spingerti?

Prova a ragionarci, prima di leggere la soluzione nel prossimo paragrafo.

Soluzioni

Raggiungere la prima riga è banale, basta una mossa:Anche raggiungere la seconda riga è piuttosto semplice, tant’è che bastano tre mosse e i pezzi utilizzati sono solo questi:

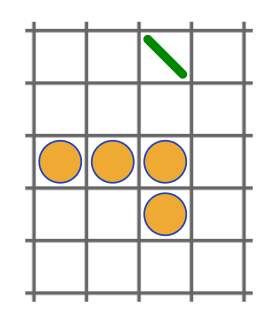
La terza riga è un po’ più difficile da raggiungere, e utilizza questi pezzi (A e B sono alternative):

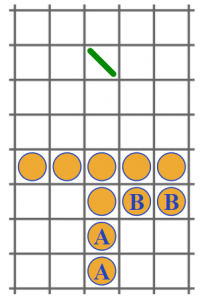
Raggiungere la quarta riga è ancora più complesso, coinvolgendo molti pezzi:

Raggiungere la quinta invece non è possibile.

Nel senso che nessuno ci è riuscito ancora?

No, si può dimostrare che, anche avendo a disposizione infinite pedine, è impossibile da raggiungere!

E perché?

La dimostrazione è elegante, ma richiede un po’ di conoscenze matematiche (e di formule). Se vuoi è qui di seguito.

Dimostrazione

L’idea di base è assegnare un certo punteggio ad ogni cella che contiene un soldato, definendo tramite la loro somma un “punteggio globale”. Tramite scelte opportune, si può mostrare che, mossa dopo mossa, il punteggio non può che diminuire. Questa caratteristica porta alla soluzione.

Chiamiamo traguardo il punto da raggiungere e indichiamolo con \(x^0=1\). Tutte le altre celle sono indicate con \(x^n\), dove n è il numero di caselle di distanza dal traguardo, muovendosi orizzontalmente o verticalmente. Il valore di x è al momento incognito, e sarà scelto opportunamente dopo aver fatto le prime considerazioni.

In questo modo, se consideriamo la configurazione iniziale di soldati, possiamo assegnare un punteggio basato sulla somma dei valori sotto ogni soldato (per esempio \(x^2+2x^3\).

Quando un soldato salta su un suo vicino, ci sono tre casi da considerare:

1. un soldato salta verso il traguardo: se il valore del soldato che salta è \(x^n\),

I soldati si trovano nelle caselle in grassetto (totale \(x^{n-1}+x^n\)). Quando quello su \(x^n\) salta ne rimane solo uno su \(x^{n-1}\).

Il punteggio cambia di \(x^{n-2}-(x^{n-1}+x^n)=x^{n-2}(1-x-x^2)\)

2. un soldato salta allontanandosi dal traguardo: se il valore del soldato che salta è \(x^n\),

I soldati si trovano nelle caselle in grassetto (totale \(x^n+x^{n+1}\)). Quando quello su \(x^n\) salta ne rimane solo uno su \(x^{n+2}\).

Il punteggio cambia di \(x^{n+2}-(x^{n+1}+x^n)=x^n(x^2-x-1)\)

3. un soldato salta lasciando invariata la sua posizione rispetto al traguardo: se il valore del soldato che salta è \(x^n\),

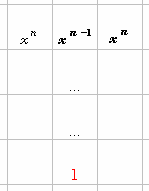
I soldati si trovano nelle caselle in grassetto (totale \(x^n+x^{n-1}\)). Quando quello su \(x^n\) salta ne rimane solo uno su \(x^n\).

Il punteggio cambia di \(x^n-(x^{n-1}+x^n)=x^{n-1}\)

Se scegliamo opportunamente il valore di x, possiamo fare in modo che il punteggio per il primo tipo di salto resti invariato. Poniamo quindi che il cambiamento di punteggio del primo salto sia 0:

\(x^{n-2}(1-x-x^2)=0\)

L’equazione dà come soluzioni uno zero (che non ci porta da nessuna parte), e

Prendiamo la radice minore di 1, quella con il meno,

È l’inverso del numero aureo. Data la scelta di x, ora sappiamo che

e di conseguenza

Con questa scelta:

1. un salto verso il traguardo porta ad un cambiamento del punteggio totale iniziale pari a zero.

2. un salto allontanandosi dal traguardo porta ad un cambiamento di \(\varphi^2-\varphi-1=-2\varphi\), minore di zero.

3. un salto restando invariati rispetto al traguardo porta ad un cambiamento di \(-\varphi^{n-1}\), anche questo minore di zero.

Il punteggio totale iniziale quindi non può aumentare.

Si può raggiungere il traguardo, che ha punteggio 1, esclusivamente se la somma dei punteggi delle caselle su cui sono inizialmente i soldati è maggiore di 1.

Come primo caso, poniamo il traguardo sulla prima riga sopra la linea orizzontale; conosciamo la soluzione in questo caso. Consideriamo il massimo punteggio iniziale, che si ha quando tutte le caselle sotto sono occupate:

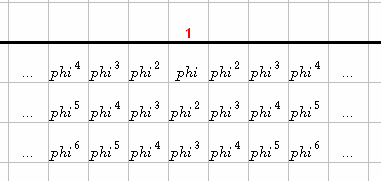
La somma dei punteggi della prima riga sotto il traguardo è

Sommando gli infiniti membri in parentesi, e utilizzando le proprietà di​ \(\varphi\), i termini si cancellano tutti tranne l’uno. Quindi la somma tra parentesi è esattamente pari a 1.

Per quanto riguarda la linea sottostante, si ragiona allo stesso modo, moltiplicando per un fattore \(\varphi\), e così anche per tutte quelle sotto. La somma totale di tutte le caselle è quindi

Utilizzando il calcolo fatto in precedenza e le proprietà di \(\varphi\) si può semplificare in

Il punteggio finale di questa configurazione è quindi \(5+3\varphi\), che è maggiore di uno.

È quindi possibile raggiungere la prima riga (o meglio, non è impossibile a priori, ma abbiamo già visto che si può effettivamente risolvere).

Il successivo caso da considerare è quello del traguardo posto sulla seconda riga. In questo caso ogni quadrato sotto la riga è distante uno in più dal traguardo di quanto non lo fosse al punto precedente. Il nuovo punteggio si trova quindi moltiplicando il vecchio per \(\varphi\).

​Allo stesso modo per le righe successive:

\(S_3=2+\varphi\)

\(S_4=1+\varphi\)

\(S_5=1\)

Nell’ultimo caso, quando il traguardo è posto sulla quinta riga il punteggio totale è esattamente 1!

Dato che le mosse abbassano il punteggio iniziale, è impossibile che si riesca a raggiungere la quinta riga!

Davide Palmigiani