Il Giappone è stata una rivelazione di questa coppa del mondo. E torna alla mente dei tifosi la saga di “Holly e Benji”. E la domanda: Ma quanto è lungo il loro campo? Ce ne parlano Marco Menale e Alberto Saracco.
Si è concluso agli ottavi di finale il mondiale di calcio in Qatar del Giappone. I “Samurai Blu” si sono arresi alla Croazia, ma solo ai rigori, dopo l’1-1 dei 120 minuti di gioco. Tuttavia è una delle squadre che più ha sorpreso. Ha superato un girone infernale con Spagna e Germania, riuscendo a battere entrambe per 2-1, partendo sempre da una situazione di svantaggio. E siamo diventati un po’ tutti tifosi del Giappone. Sulle note del coro “Vamos Nippon”, i goal di Doan e le parate di Gonda ci hanno riportati a loro: Holly e Benji. Le falcate infinite, le partite che vedono alternarsi le stagioni e i continui flashback palla al piede, come cantano i Gem boy. E soprattutto è tornata la domanda delle domande: ma quanto è lungo il campo di Holly e Benji?
Facciamo un po’ di conti, assumendo la Terra sferica. La figura 1 è una rappresentazione geometrica della scena di gioco. Ricordiamo che Holly comincia a vedere la porta dalla metà campo (il video in fondo all’articolo per i dettagli). Dunque nel punto \(F\), a metà campo, si trova Holly (o meglio gli occhi), mentre in \(D\) la traversa della porta difesa da Benji. Con \(R\) indichiamo il raggio quadratico medio della Terra, pari a \(6371\, km\). Inoltre \(h_1\) rappresenta l’altezza di Holly, pari a \(1,30\, m\) (parliamo di bambini di 10 anni), e \(h_2=2,44\, m\) l’altezza della porta.
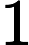
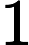
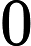
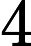
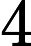
Figura 1. Rappresentazione sulla superficie terrestre del campo di Holly e Benji, realizzata in GeoGebra.
Guardiamo ancora la figura 1. Nel nostro caso, le tangenti alla circonferenza nel punto \(G\) approssimano gli archi della stessa circonferenza. Dunque la lunghezza della metà campo, data dall’arco di \(\overset\frown{BC}\), è approssimata dalla lunghezza d del segmento \(\overline{DF}\). Dal teorema di pitagora:
\[l^2=2Rh+h^2,\]
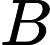
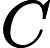
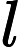
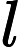
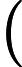
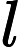
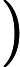
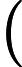
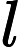
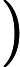
dove \(l\) e \(h\) sono i valori \((l_1, h_1)\) e \((l_2, h_2)\).
Tuttavia \(h\) è trascurabile rispetto a \(R\), essendo molto più piccolo, dunque assumiamo:
\[l^2=2Rh.\]
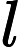
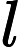
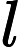
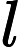
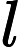
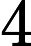
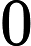
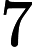
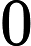
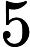
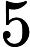
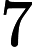
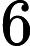
Troviamo cosi i valori di \(l_1\) e \(l_2\):
\[\begin{align*}
l_1&=\sqrt{2Rh_1}=4070\, m,\\
l_2&=\sqrt{2Rh_2}=5576\, m.
\end{align*}\]
E quindi:
\[d=l_1+l_2=9646.\]
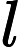
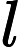
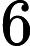
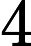
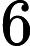
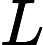
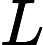
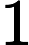
Pertanto la lunghezza \(L\) dell’intero campo è:
\[L=2d=19292\, m.\]
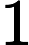
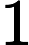
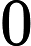
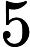
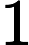
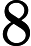
Ebbene sì, siamo oltre i \(19\, km\) di campo. E considerando che un campo regolamentare è lungo in media \(105\, m\), allora il campo di Holly e Benji è pari a più di \(183\) campi da calcio regolamentari. Ecco perché nell’attraversare la metà campo Holly riesce a ripensare alla sua intera vita.
Nel ragionamento adottato abbiamo fatto delle approssimazioni. Ad esempio non esiste un raggio della terra, essendo questa più uno sferoide. Considerando raggio polare e raggio equatoriale, otteniamo una stima dal basso e una dall’alto per avere un intervallo di variabilità di 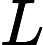\(L\).
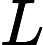
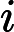
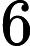
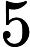
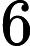
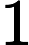
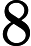
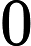
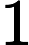
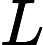
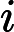
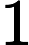
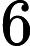
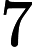
Per la stima dal basso, diciamo \(L_{min}\), consideriamo il raggio polare \(R=6356\, km\). L’altezza della porta \(h_2=1,80\, m\), ossia quella per bambini, e l’altezza di Holly \(h_1=1\, m\). Con lo stesso ragionamento, otteniamo:
\[L_{min}=2(\sqrt{ 2Rh_1}+\sqrt{Rh_2})=16,7\, km.\]
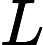
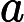
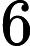
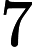
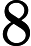
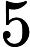
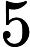
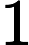
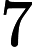
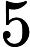
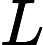
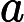
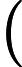
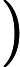
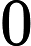
Per la stima dall’alto, \(L_{max}\), consideriamo il raggio equatoriale \(R=6378\, km\). L’altezza della porta \(h_2=2,55\, m\) e un Holly più adulto, alto \(h_1=1,75\, m\). E così:
\[L_{max}=2(\sqrt{ 2Rh_1}+\sqrt{Rh_2})=20,9\, km.\]
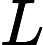
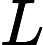
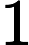
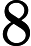
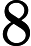
In definitiva la lunghezza \(L\) del campo di Holly e Benji si stima:
\[L=18,8 \pm 2\, km.\]
Mistero svelato. E considerando la sconfitta ai rigori, forse i giapponesi non sono abituati a una distanza dalla porta di appena \(11\, m\).
