Quando possiamo tornare a usare un calendario inutilizzato del 2020? E degli altri anni? Ce lo dice Raffaella Mulas in questo episodio de “La matematica danzante”.
da Raffaella Mulas | 1 Gennaio 2021 | Divulgazione, La matematica danzante | 3 commenti
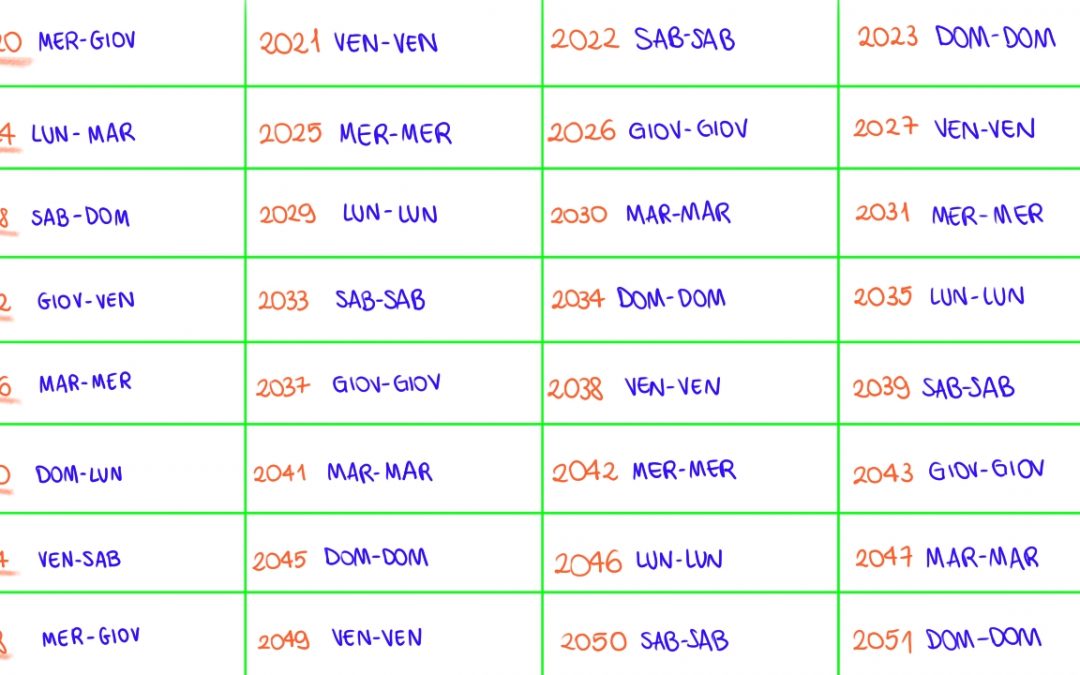
Quando possiamo tornare a usare un calendario inutilizzato del 2020? E degli altri anni? Ce lo dice Raffaella Mulas in questo episodio de “La matematica danzante”.








Here’s the […]
In un paese […]
A short book […]
The next issue […]
Here’s the […]
Here’s the […]
Salve
Ho seguito la regola andando indietro
Quindi 2021-2010-1999-1993
E torna
Ma non capisco, oppure sbaglio,il perche’ il 1900 essendo non divisibile per 4 .
I calendari del 1999 e 1993, sono identici al 2021
Forse non ho capito?
Buongiorno,
grazie mille per questo intervento interessante. Avrei due domande: innanzitutto è possibile dimostrare che il ciclo è sempre di 28 anni? E che il sotto-ciclo dei non bisestili è 6 -11-11? Intuitivamente capisco la ragione di questi numeri, ma mi piacerebbe un po’ di formalismo già pronto, per la pigrizia di non dover costruire la dimostrazione 😉
Inoltre, per poter riutilizzare un’agendina è necessario che anche la Pasqua sia coincidente nei due anni considerati. Mi sono posta il problema perché effettivamente ho riutilizzato una vecchia agenda e nel mio caso la data della Pasqua era la stessa. Questo accade sempre? O solo in determinati casi? E se è vera la seconda ipotesi, in quali casi? Anche qui, capisco che si tratti di far combaciare calendario lunare e solare, tenendo presente le regole per il calcolo della Pasqua, ma mi piacerebbe avere qualcosa di più solido.
Grazie per l’attenzione.
Salve,
per quanto riguarda la coincidenza della Pasqua, questa non si verifica sempre (per esempio è stata l’11 aprile nel 1993 e sarà il 4 aprile nel 2021), ma non saprei trovare un modo per specificare quando accada.
Come dimostrazione del ciclo e dei sotto-cicli, una volta verificati direttamente su una qualsiasi sequenza di 28 anni (per esempio quella nello schema del video), basta osservare che ci sono due anni indistinguibili, sia dal punto di vista della corrispondenza tra date e giorni della settimana sia per la posizione rispetto a un anno bisestile (per esempio il 2020 e il 2048): a questo punto, dato che gli anni di partenza sono equivalenti, spostandosi indietro nel tempo a partire dal primo di questi anni oppure in avanti a partire dal secondo, i giorni degli anni non potranno che ripetersi nello stesso modo, per cui verrà sempre ripetuto lo schema iniziale di 28 anni; sempre a patto di non considerare anni secolari non divisibili per 400.
Spero che questa spiegazione sia chiara e soddisfacente 🙂