Questa è una libera traduzione di Giuseppe Pipoli  dell’articolo Demarrage Trompeur di Patrick Popescu-Pampu apparso su  Images de Mathématiques 27 dicembre 2017.
 

 

Qual è il termine successivo della sequenza 2, 4, 8 ,16? Credete di saperlo? Calma, non così in fretta… Disegnamo un cerchio e prendiamo due punti sulla circonferenza, tracciamo quindi la corda che li unisce:

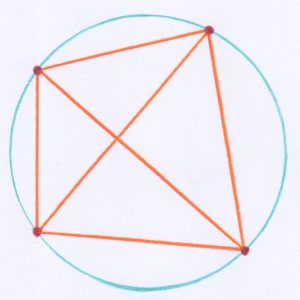
In quante regioni la corda divide il cerchio? Evidentemente in 2. Prendiamo ora 3 punti su una circonferenza e tracciamo tutte le corde che li congiungono.

In quante regioni risulta suddiviso il cerchio? Non è difficile contarle: sono 4. Consideriamo ora 4 punti… Questa volta individuiamo 8 regioni.

E se scegliamo 5 punti? Abbiamo finora trovato la sequenza 2, 4, 8, c’è la forte tentazione di dire che il termine successivo è 16. Facciamo il disegno per esserne sicuri:

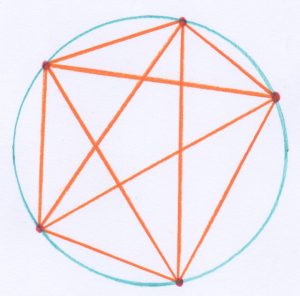
Ebbene sì, sono proprio 16… Allora se prendiamo n punti sulla circonferenze e li congiungiamo in tutte le maniere possibili, probabilmente conteremo $$2^{n-1}$$ regioni nel cerchio, e questo potrà certamente essere provato per induzione senza troppa difficoltà…

Questa è stata la reazione di tutti i colleghi matematici a cui ho mostrato la sequenza delle figure precedenti. Non sembravano troppo interessati…

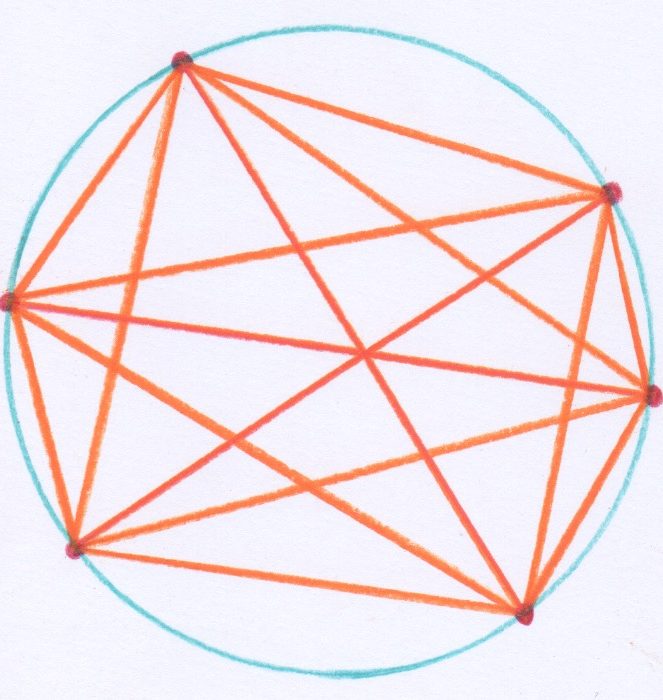
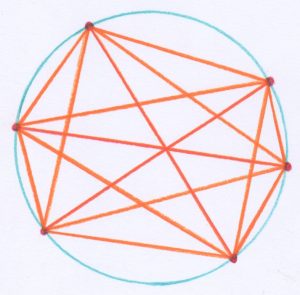
Aspettate – gli rispondevo – e contate le regioni che si ottengono per $$n$$ uguale a 6:

Non è più così facile, vero?  Bisogna concentrarsi per trovare una strategia…bisogna essere sicuri di contare ogni regione… ma ognuna una sola volta… mi sono sbagliato, ho ottenuto 31 regioni… possibile? Ricomincio…ancora 31…31? Non dovevano essere 32?

Eh no! Sono solamente 31. Notiamo però che bisogna scegliere i punti sulla circonferenza in modo che non esistano 3 corde che si incontrano in uno stesso punto interno al cerchio, altrimenti troveremo ancora meno regioni.

La nostra sequenza continua quindi così:

2, 4, 8, 16, 31.

Riuscite ad indovinare l’elemento successivo? Non è per niente facile, sono d’accordo…

Il libro dei numeri

Prima di indicarvi la risposta, vorrei svelarvi la mia fonte per questo problema. Si tratta dell’opera Il libro dei numeri  di John H. Conway e Richard K. Guy pubblicato nel 1999 da Hoepli, traduzione italiana di The book of numbers pubblicato nel 1996 da Copernicus.

E’ stato molto piacevole leggere questo libro. Non è una raccolta di problemi, ma un racconto che accompagna il lettore nel mondo dei numeri, da quelli naturali fino ai numeri surreali introdotti da Conway, uno degli autori. Sono esposte tante proprietà insolite più o meno famose dei numeri e delle sequenze di numeri. Queste proprietà vengono dimostrate se non è troppo complicato farlo. Il ritmo è sostenuto, a volte lascia senza fiato. Una volta aperto questo libro non ho potuto fermarmi fino a quando non l’ho finito.  Lo raccomando a chiunque apprezzi i racconti matematici e a tutti gli insegnanti di scuola superiore che sono alla ricerca di idee per animare dibattiti durante le ore di matematica.

Una dimostrazione dell’irrazionalità

Possiamo trovarci delle storie accessibili ai liceali? Certamente sì. Ecco un esempio di come Conway e Guy spiegano l’irrazionalità di $$\sqrt{n}$$, per tutti i naturali n che non sono quadrati perfetti. Supponiamo per assurdo che $$\sqrt{n}$$ sia razionale. Allora possiamo trovare due interi positivi A e B tali che

$$n=\left(\frac AB\right)^2.$$

Questa uguaglianza può essere riscritta così:

$$\frac AB =\frac{nB}{A}.$$

Si tratta di un’uguaglianza tra due numeri razionali che non sono interi. Dunque anche le loro parti frazionarie coincidono, questo significa che esistono due interi positivi a e b tali che

$$\frac aB = \frac bA,$$

e inoltre

e inoltre $$a<A$$ e $$b<B$$.  L’ultima uguaglianza è equivalente a

$$\frac ab = \frac AB.$$

Abbiamo allora trovato una nuova frazione per $$\sqrt{n}$$ con un numeratore e un denominatore strettamente più piccoli di quelli della frazione originaria $$\frac AB$$. Continuando così, si ottengono delle successioni infinite e strettamente decrescenti di interi positivi, arrivando chiaramente ad un assurdo. Pertanto $$\sqrt{n}$$ è irrazionale…

Ritorno alle corde

Ecco la risposta alla domanda che vi ho posto all’inizio.

Teorema. Il numero di regioni nelle quali risulta decomposto l’interno di un cerchio dalle corde che congiungono n punti sulla circonferenza (scelti in modo tale che non esistono 3 corde passanti per lo stesso punto interno) è pari a

$${n-1\choose 0} + {n-1\choose 1} + {n-1\choose 2} + {n-1\choose 3} + {n-1\choose 4}.$$

L’espressione $${n-1\choose k}$$ indica il numero di sottoinsiemi aventi k elementi in un insieme che ne ha n-1.

 

Come si può dimostrare questo Teorema? Il metodo proposto nel libro di Conway e Guy consiste nel numerare i punti sulla circonferenza da 0 a $$n-1$$ in senso, per esempio, antiorario, e di associare ad ogni regione una etichetta che è un sottoinsieme formato da al più 4 elementi dell’insieme $$\{ 1,2,\dots,n-1 \}$$. Il metodo per assegnare le etichette è spiegato dagli autori nella figura seguente:

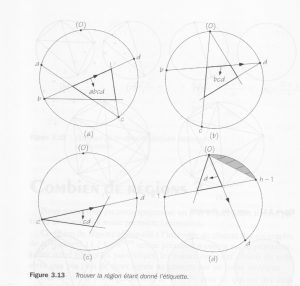
Per esempio, per i piccoli valori di $$n$$ considerati poc’anzi, otteniamo la codifica seguente delle regioni (alle regioni ombreggiate si associa l’insieme vuoto):

 

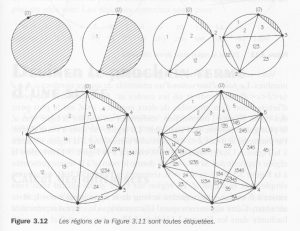
L’osservazione chiave è che, in questa maniera, abbiamo creato una biezione tra le regioni e i sottoinsiemi con al più 4 elementi di $$\{ 1,2,\dots,n-1\}$$. Così facendo, per $$n$$ minore di 6, otteniamo tutti i possibili sottoinsiemi di $$\{ 1,2,\dots,n-1\}$$. Questo spiega come mai in questi casi troviamo esattamente $$2^{n-1}$$ regioni.

Siete d’accordo con me che questo potrebbe essere un tema molto carino da trattare come approfondimento di matematica al liceo?