Pitagora e policromia

In questo articolo di Shalom Eliahou e Jean Fromentin, apparso originariamente su Images des Mathématiques, e qui tradotto da Elena Toscano, vedremo come degli oggetti matematici molto antichi e di natura elementare continuino a porre problemi anche ai matematici di oggi. Più precisamente ci dedicheremo al nostro passatempo preferito: colorare gli interi rispettando determinati vincoli stabiliti a priori. Un’attività ludica, sicuramente, ma anche una fonte di notevoli sfide per la ricerca matematica, come abbiamo visto in due articoli recentemente pubblicati sullo stesso sito: I numeri di Schur, centenari promettenti e Le straordinarie previsioni del Reverendo Walker

Terne pitagoriche

Iniziamo presentando gli oggetti matematici interessati dai nostri vincoli sui colori. Tali oggetti sono le terne pitagoriche, cioè terne di interi non nulli $$(a,b,c)$$ che soddisfano l’uguaglianza:

$$a^2+b^2=c^2$$.

L’esempio più semplice di terna pitagorica è $$(3,4,5)$$: si tratta infatti di interi non nulli ed è verificata l’uguaglianza $$3^2+4^2=5^2$$ dato che $$9+16=25$$.

Uno degli strumenti più potenti del pensiero matematico – o del pensiero tout court – è cercare di considerare uno stesso oggetto o concetto da punti di vista differenti. I matematici ne fanno un uso intensivo traendone grande beneficio. Ad esempio, i legami intimi tra algebra e geometria sono una fonte fantastica di arricchimento reciproco tra queste due branche della matematica.

Interpretazione geometrica

Le terne pitagoriche, per l’appunto, possono essere considerate allo stesso tempo [1] come oggetti algebrici – o aritmetici – e geometrici. Dal punto di vista geometrico, ovviamente, sono strettamente legate al Teorema di Pitagora relativo alle lunghezze dei lati dei triangoli rettangoli.

A titolo di esempio, la figura seguente rappresenta la terna pitagorica $$(3,4,5)$$. I due cateti di questo triangolo rettangolo sono di lunghezza 3 e 4 rispettivamente, mentre l’ipotenusa è di lunghezza 5:

Oltre a $$(3,4,5)$$, vi sono altre terne pitagoriche? In altre parole, altri triangoli rettangoli i cui tre lati siano tutti di lunghezza intera?

L’umanità è interessata a questo problema da almeno 3800 anni, ben prima di Pitagora, come testimonia la famosa tavoletta di argilla Plimpton 322:

Un articolo di Christine Proust è dedicato a questa tavoletta di argilla e alla sua interpretazione.

Infinità

Ebbene sì, ci sono molte altre terne pitagoriche. È facile produrne di nuove a partire da $$(3,4,5)$$, per esempio $$(6,8,10)$$ come è facile verificare. È bastato moltiplicare tutto per 2. Questo è peraltro un principio generale: per ogni numero naturale n, la terna $$(3n,4n,5n)$$ è pitagorica.

Dimostrazione: (clicca per leggerla)

$$(3n)^2+(4n)^2=9n^2+16n^2=25n^2=(5n)^2$$

Esiste dunque un’infinità di terne pitagoriche. Detto ciò, geometricamente, non vi è quasi alcuna differenza tra le terne $$(3,4,5)$$ e $$(3n,4n,5n)$$ dato che i corrispondenti triangoli rettangoli sono simili. Ciò è chiaramente visibile nella figura seguente che rappresenta la terna $$(6,8,10)$$:

Ora, vi sono altre terne pitagoriche, oltre a $$(3n,4n,5n)$$, che sono geometricamente differenti? Sì. Per esempio $$(5,12,13)$$ che è pitagorica poiché:

$$5^2+12^2=25+144=169=13^2$$

e il corrispondente triangolo rettangolo è molto diverso da quello che rappresenta la terna $$(3,4,5)$$:

Vi è dell’altro? Cosa notevole, esiste un’infinità di terne pitagoriche geometricamente distinte a due a due e sono tutte note! La loro descrizione completa è data più avanti.

Presentazione del gioco

Uno degli scopi di questo articolo è quello di attirare l’attenzione dei lettori su un aspetto affascinante delle terne pitagoriche: non solo interessano l’umanità da millenni ma, ancora oggi, pongono enormi sfide alla ricerca matematica. Il gioco di colorazione che stiamo per spiegare lo testimonia abbondantemente.

Ecco le regole di questo gioco. Esso è di natura collaborativa, l’unico obiettivo è ottenere il miglior punteggio possibile N.

Regola 1: si colorano gli interi $$1,2,3,4,\dots $$ con due colori, diciamo rosso e blu.
Regola 2: affinché una colorazione degli interi $$1,2,3,4,\dots N$$, sia accettata, ogni terna pitagorica $$(a,b,c)$$ i cui componenti non superino N deve essere mista, ovvero comprendere sia un membro rosso che un membro blu.
Regola 3: il punteggio di una data sessione di gioco è il più grande N raggiunto rispettando le regole 1 e 2.

Inventato diversi decenni fa, questo gioco continua a mobilitare i ricercatori per determinare la o le migliori strategie. In particolare, ci si augura di poter rispondere alle seguenti domande fondamentali:

Come ottenere un punteggio N che sia il più elevato possibile?
C’è un punteggio massimo, vale a dire un punteggio che non può essere superato?

Ecco i migliori punteggi ottenuti negli ultimi dieci anni, prevalentemente frutto di intensi lavori di squadra.

Generazione delle terne pitagoriche

Come osservato prima, vi sono un’infinità di terne pitagoriche e, inoltre, le conosciamo tutte. Come descrivere questa collezione infinita? Grazie alla potenza della parametrizzazione. In altre parole, possiamo ottenere tutte le terne pitagoriche $$(a,b,c)$$ grazie a formule che esprimono $$a, b, c$$ in termini di tre parametri formali $$u, v, n$$ arbitrariamente scelti. Ecco la regola nota sin dall’antichità.

Regola. Ogni terna pitagorica $$(a,b,c)$$ può essere ottenuta nel seguente modo. Scegliere tre numeri naturali qualunque u, v, n, con u strettamente maggiore di v, e imporre che:

$$a=n \times (u^2-v^2)$$, $$b=n\times 2uv$$, $$c=n\times (u^2+v^2)$$.

Per esempio, la nostra terna preferita $$(3,4,5)$$ si ottiene con la suddetta regola ponendo $$u=2$$, $$v=n=1$$.

Traccia della dimostrazione (clicca per leggerla)

L’ingrediente principale per conseguire questo risultato è la fattorizzazione, unica a meno dell’ordine dei fattori, di un intero naturale nel prodotto di numeri primi. Ad esempio $$60=2^2\times 3\times 5$$.

Se $$(a,b,c)$$ è una terna pitagorica, allora soddisfa $$a^2+b^2=c^2$$, quindi anche $$b^2=c^2-a^2$$. Sapendo che $$c^2-a^2=(c+a)\times ((c-a)$$, otteniamo l’uguaglianza:

$$b^2=(c+a)\times (c-a).$$

Il resto della dimostrazione consiste nell’analizzare e confrontare le rispettive fattorizzazioni di $$b^2$$ e di $$(c+a)\times (c-a)$$ come prodotto di numeri primi e utilizzare il fatto che essi sono sostanzialmente identici.

Fino a 20

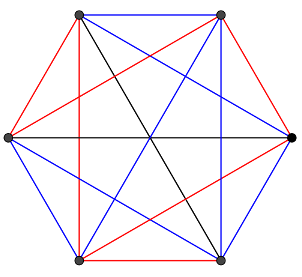
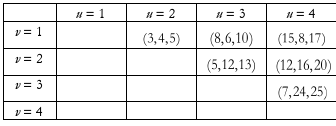
Determiniamo ora la collezione C di tutte le terne pitagoriche costituite da interi naturali inferiori o uguali a 20. Per fare ciò abbiamo una regola quindi usiamola! Si tratta di scegliere dei numeri interi naturali u, v, n con $$u>v$$ in modo che i termini restino inferiori a 20.

Sapendo che $$c=n(u^2+v^2)$$ e che i quadrati crescono molto velocemente, i soli valori ammissibili per u e v sono 1, 2, 3, 4. Infatti, già il 5 non è più adatto dato che $$5^2$$ è maggiore di 20. Le tabelle che seguono riportano le diverse terne ottenute quando u e v scorrono tra 1, 2, 3, 4.

Per $$n=1$$ otteniamo la tabella seguente. Gli spazi vuoti corrispondono ai valori di u e v che non verificano la condizione richiesta $$u>v$$.La terna (7,24,25) è da escludere poiché 24 e 25 sono maggiori di 20.

Per $$n=2$$, non otteniamo nuove terne ammissibili di C.
Per $$n=3$$, otteniamo una sola nuova terna in C ovvero $$(9,12,15)=3\times (3,4,5)$$.

Per $$n=4$$ la sola terna $$(12,16,20)$$ è ammissibile in C ma è già stata ottenuta per $$n=1$$.

Per quanto riguarda valori superiori di n, essi darebbero terne troppo grandi e quindi non in C. Dunque la nostra ricerca è terminata! L’insieme C delle terne pitagoriche tra 1 e 20 è composto dai sei membri seguenti:

$$C=(3,4,5),(5,12,13),(6,8,10),(8,15,17),(9,12,15),(12,16,20)$$.

Ecco una rappresentazione dei triangoli rettangoli corrispondenti:

Un punteggio di 20

Vediamo ora come ottenere al nostro gioco un punteggio di 20. Dobbiamo colorare in rosso o in blu ogni numero intero compreso tra 1 e 20 in modo che tutte le terne in C siano miste. Osserviamo innanzitutto che gli interi 1, 2, 7, 11, 14, 18 e 19 non figurano in nessuna terna di C; non vi è quindi alcun vincolo sulla scelta dei loro colori. Poiché (3,4,5) appare in C, deve essere mista, quindi 3, 4 e 5 non devono essere dello stesso colore. Ad esempio, colorando 3 e 4 in blu e 5 in rosso:

C = (3,4,5), (5,12,13), (6,8,10), (8,15,17), (9,12,15), (12,16,20).

Per la seconda terna scegliamo di colorare 12 e 13 in blu:

C = (3,4,5), (5,12,13), (6,8,10), (8,15,17), (9,12,15), (12,16,20).

Per la quinta e sesta terna scegliamo di colorare 9 e 16 in blu e 15 e 20 in rosso:

C = (3,4,5), (5,12,13), (6,8,10), (8,15,17), (9,12,15), (12,16,20).

Terminiamo colorando, per esempio, 6 e 8 in blu e 10 e 17 in rosso:

C = (3,4,5), (5,12,13), (6,8,10), (8,15,17), (9,12,15), (12,16,20).

La colorazione

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15, 16, 17,18,19,20

in cui i numeri in nero sono colorati indifferentemente in rosso e in blu, soddisfa le regole del gioco e produce un punteggio di 20.

Migliorare il punteggio

Ottenere un punteggio di 20 è stato piuttosto semplice. È possibile migliorarlo lavorandoci un po’ di più. Provate dunque a ottenere un punteggio di 50.

Un piccolo aiuto per iniziare (clicca per vederlo)

Ecco, per iniziare, l’insieme delle terne pitagoriche fino a 50:

(3,4,5), (5,12,13), (6,8,10), (7,24,25), (8,15,17), (9,12,15), (9,40,41), (10,24,26), (12,16,20), (12,35,37), (14,48,50), (15,20,25), (15,36,39), (16,30,34), (18,24,30), (20,21,29), (21,28,35), (24,32,40), (27,36,45), (30,40,50).

L’apparente semplicità di questo gioco è fuorviante. Arrivare fino a 20 o a 50 è ancora possibile ma il gioco si complica abbastanza rapidamente: le scelte di colori che facciamo all’inizio finiscono per interrompere il gioco, vale a dire portano a terne pitagoriche non miste ossia monocromatiche; dobbiamo quindi esplorare nuove scelte per sperare di evitare ciò e puntare più in alto.

Per veder figurare i loro nomi nella tabella dei punteggi migliori i nostri campioni hanno dovuto fare ricorso a metodi molto sofisticati e all’uso intensivo di computer.

Più precisamente (clicca per vederlo)

Il metodo utilizzato dai team 1, 2 e 4 è quello di riformulare in modo intelligente il gioco in termini di un problema di soddisfacibilità booleana – o problema SAT – e di risolvere questo nuovo problema mediante un adeguato solutore con un computer.

Il metodo usato dal nostro campione numero 3 è leggermente diverso. Si basa su un metodo probabilistico per esplorare le possibili diverse colorazioni [6].

Policromia e trappole

Il nostro gioco è tipico di una teoria chiamata Teoria di Ramsey dovuta a un giovane e geniale matematico inglese morto prematuramente, Frank Plumpton Ramsey [1903-1930]. Prima della nascita di questa teoria intorno al 1929, avevano già visto la luce due primi esempi che la prefiguravano, uno dovuto a David Hilbert nel 1892 e l’altro di Issai Schur nel 1916. Nella sua forma più generale, si tratta del seguente problema: partiamo da un certo oggetto matematico, coloriamo i suoi elementi costitutivi con un numero fissato di colori e ci chiediamo se troveremo necessariamente un sotto-oggetto della stessa natura che sia monocromatico, ovvero i cui elementi costitutivi siano tutti dello stesso colore.

Ad esempio, consideriamo il grafo completo con 6 vertici e coloriamo arbitrariamente gli archi in due colori, rosso e blu. Un risultato fondamentale della Teoria di Ramsey dice che necessariamente vedremo emergere un triangolo monocromatico, con i suoi tre lati tutti rossi o tutti blu. A titolo illustrativo, ecco un possibile modo di colorare parzialmente un grafo di questo tipo senza che emerga alcun triangolo monocromatico a questo stadio:

Mancano solo due archi neri da colorare. Ma non appena si colorano l’uno o l’altro in rosso o in blu, emerge un triangolo monocromatico. Questo è inevitabile, anche a partire da una qualsiasi altra colorazione parziale, come dimostrato dalla teoria. Di contro, dato il grafo completo con soli 5 vertici, è possibile colorarne gli archi con due colori evitando qualsiasi triangolo monocromatico. Provate e vedrete!

C’è un punteggio massimo?

Torniamo al nostro gioco e alla domanda fondamentale posta all’inizio: il gioco ammette, sì o no, un punteggio massimo? Il matematico Ronald Graham aveva persino proposto una ricompensa di 100 dollari per la prima persona che avrebbe risposto a questa domanda.

Per stabilire l’esistenza di un punteggio massimo M, è necessario dimostrare che, quale che sia la colorazione a due colori degli interi $$1,2,\dots , M+1$$ vi sarà necessariamente almeno una terna pitagorica $$(a,b,c)$$ con a, b, c compresi tra 1 e $$M+1$$ che sarà monocromatica ovvero o tutta rossa o tutta blu.

Nulla dice a priori che un tale punteggio massimo esista. Come abbiamo visto all’inizio, attualmente il punteggio migliore è 7824, ottenuto nel 2016 dalla squadra numero 1. Ma dopo tutto, forse, con un po’ di astuzia e di fortuna potremmo ottenere un punteggio maggiore o uguale al milione.

Beh no, tutta l’astuzia del mondo non sarebbe sufficiente! Perché la squadra numero 1 ha fatto ben più che ottenere il punteggio di 7824: ha dimostrato, con calcoli al computer tanto massivi quanto audaci, che il punteggio di 7825 è impossibile da raggiungere. In altre parole, il nostro gioco ammette un punteggio massimo M che è esattamente

M = 7824.

La colorazione ammissibile dei numeri interi da 1 a 7824 ottenuti dalla squadra numero 1 è visibile qui.

Dimostrazione di massimalità

Come convincersi che il punteggio di 7825 è irraggiungibile? È estremamente difficile, per dire impossibile, senza un computer allo stato attuale delle nostre conoscenze. Anche per un computer non è esattamente una passeggiata! La dimostrazione fornita dal nostro team vincente si basa su un calcolo eseguito utilizzando un solutore SAT su un super-computer di 800 core – ossia circa 200 computer ad alte prestazioni di quelli attualmente sul mercato – per 2 giorni.

Per spazzare via ogni dubbio sulla validità della loro affermazione, gli autori hanno accompagnato il loro calcolo con una certificazione [7] che ne dimostra la correttezza. Peccato che questa certificazione pesi 200 Terabyte [8] – ossia la capacità di 100 dischi rigidi da 2 Terabyte come quelli di cui sono dotati i computer attuali – ma può essere tranquillamente compressa in un file di 68 Gigabyte [9]. Una bazzecola.

Detto questo, il loro lavoro pone brillantemente fine al nostro gioco. La squadra numero 1 sarà quella vincente per sempre. Per la cronaca, ha ricevuto da Ronald Graham la ricompensa promessa di 100 dollari.

Passiamo a tre colori

Per non fermarci qui, modifichiamo la Regola 1 passando a tre colori e riformuliamo la Regola 2 per far fronte a questa nuova situazione.

Regola 1 (variante): coloriamo gli interi 1, 2, 3, 4,… con tre colori, diciamo rosso, blu e verde.
Regola 2: affinché una colorazione degli interi 1, 2, 3,…, N sia accettata, ogni terna pitagorica $$(a,b,c)$$ i cui costituenti a, b, c non superino N deve essere mista, ovvero contenere almeno due colori distinti.

La Regola 3 che definisce il punteggio N di una sessione di gioco rimane la stessa. Seguendo una particolare strategia [10], Virginie Marion-Poty, Denis Robillard e i sottoscritti hanno ottenuto nel 2016 il punteggio di 4632 in questo nuovo gioco.

La strategia impiegata impone ulteriori vincoli sulla colorazione considerata. È stato possibile stabilire che il punteggio così raggiunto di 4632 è massimo all’interno di questo quadro limitato. Ecco un’immagine della colorazione ottenuta.

Dato che una colorazione a due colori è un caso particolare di quella a 3 colori, i punteggi ottenuti con la regola originale restano validi. Come nel caso di due colori, possiamo chiederci se esiste un punteggio massimo. In caso affermativo, allora deve certamente essere ben al di sopra di 7824 – e anche di 11066 – come dimostreremo di seguito.

Ecco l’attuale tabella di punteggi per la nostra variante di gioco a tre colori.

Giustificazione del punteggio di 11066 (clicca per vederlo)

Come e quando è stato ottenuto questo record di 11066 punti per la variante di gioco a tre colori? Proprio durante il processo di correzione di questo articolo, semplicemente. Ecco la storia. Il 9 Giugno 2017 alle 17:14, Adriano Marmora, revisore molto attento, scrive per chiederci se non sia possibile migliorare, nel caso di tre colori, il punteggio massimo stabilito per due colori, nel modo seguente: si parte da una colorazione rosso e blu che stabilisce il punteggio di 7824, e si colora in verde il numero 7825 e “qualche altro”. Questo, ci dice Adriano, dovrebbe sicuramente dare una colorazione accettabile.

Ebbene sì, ha perfettamente ragione! Infatti, se si colorano di verde tutti i numeri naturali compresi tra 7825 e 11066, allora la risultante colorazione in rosso, blu e verde dei numeri naturali compresi tra 1 e 11066 è perfettamente accettabile.

Ecco perché. Se $$(a,b,c)$$ è una terna pitagorica all’interno di questo intervallo, supponiamo con $$a\leq b$$, allora:

o $$a,b,c\leq7824$$ e in questo caso $$(a,b,c)$$ è colorata in rosso e blu ed è mista per costruzione;
o $$a\leq7824$$ e $$c\geq 7825$$, nel qual caso la terna è mista poiché c è verde e a è rosso o blu;
o infine $$a,b\geq 7825$$. Ma questo caso è escluso. Infatti $$c^2=a^2+b^2\geq 2\times 7825^2$$; prendendo la radice quadrata da ogni lato, si ha $$c\geq \sqrt{2}\times 7825$$ e dunque $$c\geq 11066$$ contrariamente all’ipotesi.

Ed è così che stabiliamo questo punteggio, praticamente senza colpo ferire. Grazie ad Adriano Marmora per il suo eccellente suggerimento!

È d’obbligo concludere con una congettura che sorge del tutto naturale alla luce del caso dei due colori. Per quanto tempo rimarrà aperta? Senza dubbio per un numero elevato di anni che si spera solo non tenda all’infinito.

Congettura. Esiste anche un punteggio massimo per la variante a tre colori del gioco delle terne pitagoriche.

Avviso agli appassionati!

Post-scriptum:

Gli autori ringraziano Bruno Martin e i revisori Mazoit, Aurélien Djament, Adriano Marmora, ZRIR e Ophélie Rouby per la loro attenta lettura e i loro commenti molto costruttivi sulle versioni preliminari di questo articolo.

Articolo a cura di Shalom Eliahou, traduzione dal francese di Elena Toscano

Per citare questo articolo in originale: Shalom Eliahou e Jean Fromentin — «Pythagore et mixité» — Images des Mathématiques, CNRS, 2017. On-line, URL: https://goo.gl/636G5G

NOTE

Espressione molto in voga negli ultimi tempi! [N.d.T.: si riferisce all’espressione molto usata da Macron “en même temps”, vedi ad esempio Le Monde]
Joshua Cooper, Chris Poirel, Pythagorean Partition-Regularity and Ordered Triple Systems with the Sum Property (2008), (arXiv: https://arxiv.org/abs/0809.3478).
William Kay, An Overview of the Constructive Local Lemma, (tesi: https://search.proquest.com/docview/1014404410), Università della Carolina del Sud (2012).
Joshua Cooper, Ralph Overstreet, Coloring so that no Pythagorean Triple is Monochromatic. Preprint (2015), (arXiv: https://arxiv.org/abs/1505.02222).
Marijn J.H. Heule, Oliver Kullman, Victor W. Marek, Solving and Verifying the Boolean Pythagorean Triples Problem via Cube-and-Conquer, SAT 2016, Lecture Notes in Computer Science, vol 9710 (2016), (arXiv: https://arxiv.org/abs/1605.00723).
Il metodo utilizzato è basato su una versione algoritmica del Lemma locale di Lovász (https://fr.wikipedia.org/wiki/Lemme_local_de_Lovász).
Sotto forma di file informatico: (http://satcompetition.org/2014/certunsat.shtml).
200 Terabyte ovvero duecento mila miliardi di byte!
Maggiori dettagli sono disponibili qui: https://www.cs.utexas.edu/~marijn/ptn/.
Consistente nel colorare inizialmente i numeri primi e quindi, in un secondo momento, estendere questa colorazione a tutti gli interi in modo naturale basandosi sulla loro fattorizzazione nel prodotto di numeri primi.
Shalom Eliahou, Jean Fromentin, Virginie Marion-Poty, Denis Robilliard, Are monochromatic Pythagorean triples avoidable?, Experimental Mathematics (2016), (arXiv: https://arxiv.org/abs/1605.00859)