Sofia Sabatti, della Scuola Secondaria di primo grado “Piero Calamandrei” dell’Istituto comprensivo “Cristoforo Colombo” di Chirignago, a Venezia, è risultata vincitrice quest’anno del Premio dell’UMI dedicato alla memoria di Stefania Cotoneschi docente presso Scuola Città Pestalozzi di Firenze, scomparsa nel 2015. Questo premio, consegnato oggi in occasione del XXI congresso UMI che inizia oggi a Pavia, è destinato ad un docente di ruolo di Scienze Matematiche, Chimiche, Fisiche e Naturali di scuola secondaria di primo grado, che si sia distinto per la diffusione della educazione matematica tra i giovani e più in generale nella società o nella comunità scientifica, attraverso pubblicazioni oppure opere grafiche o produzione di materiale audiovisivo o interventi su siti web. Abbiamo chiesto a Sofia di scrivere qualcosa per noi.

Mi è stato chiesto di scrivere un breve articolo per MaddMaths!, da diffondere in occasione della consegna del Premio “Stefania Cotoneschi”, su un argomento relativo alla didattica e alla mia attività di insegnante, dandomi carta bianca sul tema da scegliere, cosa che mi ha messo non poco in difficoltà.
Alla fine ho deciso di partire da un errore (mio) che mi ha confermata nell’idea che imparare la matematica è un po’ come salire una scala a chiocciola e che il lavoro di squadra (oltre che bello) è indispensabile.

Il nastro di Möbius

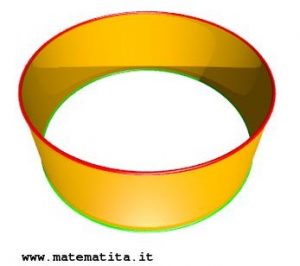
Immaginate un nastro di Möbius. Per quei pochi lettori che non ne avessero mai sentito parlare: pensate a un rettangolo (magari con i due lati corti sensibilmente più corti dei due lati più lunghi) e immaginate di incollare i suoi due lati corti uno all’altro. Se non operate alcuna torsione, ottenete un nastro cilindrico; se prima di incollare fate una mezza torsione, ottenete un nastro di Möbius. Il bordo del nastro cilindrico è costituito da due circonferenze “separate”, quello del nastro di Möbius da una sola curva chiusa semplice.

Il bordo di un cilindro. Immagine di Filippo Favale	Il bordo di un nastro di Möbius. Immagine di Filippo Favale

Se qualcuno non fosse convinto di come è fatto il bordo del nastro di Möbius, può costruire un modellino a partire da una strisciolina di carta e passare il dito (o un pennarello) lungo tutto il bordo: senza mai staccare il dito (o il pennarello) dal bordo, si ritroverà al punto di partenza avendolo percorso per intero.

Ho fatto costruire tante volte questo modellino ai miei alunni e ogni volta il nastro di Möbius li ha affascinati, per questa ed altre sue caratteristiche. L’ho sempre trovato un ottimo modo per iniziare un percorso di geometria che non fosse fatto solo di formule e calcoli, ma soprattutto di osservazione, stupore, ragionamento, comprensione. Fin qui, tutto bene, però…

Le (fantomatiche) facce delle superfici

Un’altra cosa che ho spesso chiesto ai miei alunni di fare, sempre sfruttando modellini di carta, è contare quante facce avesse il nastro cilindrico e quante facce avesse il nastro di Möbius. Se prendiamo il modellino del nastro cilindrico e incominciamo a colorarlo esternamente, senza attraversare il bordo, possiamo andare avanti fino a quando avremo colorato tutta la faccia esterna e lasciato bianca quella interna. Non riusciamo a fare la stessa cosa sul modellino del nastro di Möbius: se iniziamo a colorarlo e andiamo avanti finché è possibile senza attraversare il bordo, finiremo con il colorarlo tutto.

Passando dal modellino alla matematica, quello che per un bel po’ ho detto ai miei alunni è che il nastro cilindrico ha due facce mentre il nastro di Möbius ne ha una sola. Si tratta di una affermazione, questa, condivisa da molti. Con una veloce ricerca in internet si trovano numerosi siti in cui questa proprietà è descritta proprio con queste stesse parole. Eppure è una affermazione discutibile e me ne sono accorta solo qualche mese fa, a 45 anni suonati.

Perché non ha senso parlare di facce di una superficie

Prendiamo in mano il modellino di nastro cilindrico.

Le vediamo, le due facce: una è colorata, l’altra no. Ci sono alcuni punti del nastro che sono gialli, e altri punti del nastro che sono rimasti bianchi: se tengo il modellino tra pollice e indice, come in fotografia, il pollice tocca il nastro in un punto bianco, l’indice lo tocca in un punto ad esso corrispondente, ma sull’altra faccia, giallo. Che c’è che non va?
Nulla, fintanto che guardiamo il modellino di carta. Ma se invece pensiamo al nastro cilindrico come a una superficie, questo non ha alcun senso. Il modellino di carta è tanto sottile, certo, ma una superficie non è semplicemente sottile: una superficie non ha spessore. E allora, se trovassi il modo di tenere una superficie cilindrica tra le dita, laddove pollice, indice e superficie si toccassero, ci sarebbe un solo punto (non due, uno bianco e l’altro giallo)!
Il problema sta nel fatto che i modellini di carta del nastro cilindrico e del nastro di Möbius non sono superfici, ma oggetti tridimensionali e sono entrambi (topologicamente equivalenti a) un toro. [vedi nota [1]]

Per capire meglio che cosa fosse il modellino di carta del nastro di Möbius, ho costruito un altro modellino, ancora più spesso, fatto di DAS. Toccandolo e guardandolo diventa evidente che si tratti di un toro la cui superficie viene suddivisa in due regioni distinte, che sono entrambe (topologicamente equivalenti a delle) superfici cilindriche.

Sul modellino, posso individuare due “facce”, dando a questa espressione un significato analogo a quello che diamo all’espressione “facce di un poliedro”: regioni distinte di una superficie, che posso immaginare di colorare in modi diversi. Ma riferendomi alla superficie del nastro cilindrico di per sé, o alla superficie del nastro di Mòbius di per sé, non posso parlare di una “faccia che sta sopra” o di una “faccia che sta sotto”. [vedi nota [2]].

Come ho imparato che la superficie non ha spessore
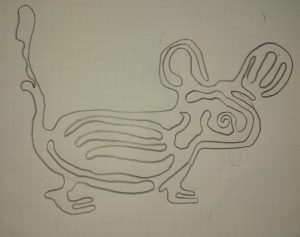
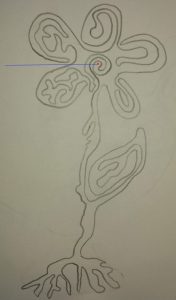
Qualche mese fa ho letto con i miei alunni Tau Topologo di Franco Ghione. Ho fatto con loro Il gioco dell’isola in esso descritto: si tratta di disegnare una curva chiusa semplice su un piano per poi colorare una delle due regioni in cui la curva divide il piano (lasciando bianca l’altra), o anche segnare nel piano un punto e stabilire se sta nella regione interna o in quella esterna alla curva, senza mettersi a colorare il tutto. Insomma: è un gioco che sfrutta il fatto che nel piano vale il teorema della curva di Jordan.

Questo topo è ciò che ha fatto Yibo quando ho chiesto ai miei alunni di disegnare una curva chiusa semplice (l’esempio che avevo fatto io alla lavagna era una circonferenza tendente ad una patata…)	Il punto rosso è nella regione esterna alla curva, quella colorata di blu. Il disegno è di Greta.	l punto rosso è nella regione esterna alla curva. Infatti la semiretta blu, che ha origine nel punto rosso e va verso l’esterno, attraversa la curva un numero pari di volte. Il disegno è di Yibo.

Abbiamo giocato al gioco dell’isola anche su una palla di polistirolo (modellino di una sfera) e su un anello di polistirolo (modellino di un toro), accorgendoci che la superficie della prima è divisa in due regioni da una qualsiasi curva chiusa semplice, mentre quella del secondo non viene divisa in due regioni per alcune curve semplici.

Ogni curva chiusa semplice disegnata su una superficie sferica, divide la superficie in due regioni distinte.	Una curva chiusa semplice disegnata sulla superficie di un toro, può dividere la superficie in due regioni distinte…
… ma può anche non farlo!

Ho chiesto ai miei alunni se, a parer loro, da questo punto di vista il nastro di Möbius si comportasse in maniera simile alla sfera o al toro: possiamo dire che ogni curva chiusa semplice presa su un nastro di Möbius lo divide in due regioni separate? O riusciamo invece a immaginare una curva chiusa semplice che non divida il nastro di Möbius in due parti?

Ero quasi certa che, a furia di tentativi e dopo aver studiato insieme il caso del toro, almeno qualcuno dei miei alunni trovasse quella che io chiamo “la linea di mezzeria” del nastro di Möbius, che sapevo non dividerlo in due parti. Alcuni alunni, in effetti, l’hanno trovata e, scorrendo il modellino tra pollice e indice, sostenevano che il nastro non fosse diviso in due regioni.

C’è stato però un gruppo di alunni che, disegnata la linea di mezzeria, ha iniziato (come ne Il gioco dell’isola) a  colorarne una parte, senza mai attraversare la curva. Mi sembrava un ottimo atteggiamento, quello di voler verificare (matita alla mano) che le cose funzionassero per davvero. Purtroppo, però, il risultato non è stato quello che mi aspettavo: sembrava proprio che il nastro di Möbius fosse diviso da questa linea in due regioni, una colorata e l’altra no…

Ho proposto allora ai ragazzi di tagliare il nastro lungo la linea di mezzeria: è stato chiaro per tutti che non si formavano due parti che si potessero separare, tenendone una nella mano destra e una nella sinistra.

Eravamo sbigottiti (io più di loro, forse): dove stavano, dopo il taglio, la regione colorata e quella non colorata? Abbiamo guardato meglio il nastro ottenuto: sembrava un po’ come il nastro cilindrico iniziale, con una faccia colorata e l’altra rimasta bianca.
Per capire che l’errore era collegato al precedente discorso sulle fantomatiche “facce”, ci ho messo un bel po’ di tempo e di energia. E non ce l’ho fatta da sola: ho dovuto stare ad ascoltare una “collega esperta”, guardare i modellini che mi ha mostrato, farne di altri e provare a raccontarle quello che man mano mi sembrava di capire. In particolare, uno dei modellini che mi hanno aiutata è stato un nastro di Möbius costruito con carta lucida:

Usando la carta lucida, si capisce bene che “quando un punto l’hai colorato, l’hai colorato”: non ce n’è un altro “opposto” che sia rimasto bianco, non ce n’è un altro su un’altra fantomatica faccia.

Morali della favola (che non è una favola)

Gli errori
“Sbagliando si impara”: lo sappiamo tutti. Forse, però, si può addirittura dire che senza sbagliare, non si impara. Senza sbagliare, si può ripetere quello che si è sentito dire da altri, si può anche raccontare una cosa di cui si è convinti, ma è molto probabile che lo si faccia senza essere scesi in profondità.
Se non avessi commesso l’errore di chiedere ai miei alunni di colorare le facce di un nastro di Möbius, e se un gruppo di miei alunni non avesse commesso l’errore di sostenere che la “linea di mezzeria” divide un nastro di Möbius in due regioni distinte, probabilmente non avrei ancora capito che cosa significhi che “Superficie è ciò che ha soltanto lunghezza e larghezza”.
Credo che dobbiamo dare ai nostri alunni l’occasione di sbagliare, mettendoli di fronte a problemi autentici, significativi e difficili, se vogliamo che imparino davvero un po’ di matematica. Con Problemi per matematici in erba, il sito che sto curando insieme alla professoressa Maria Dedò e ad alcuni altri docenti e tutor dei corsi MathUp, stiamo provando proprio a raccogliere problemi di questo tipo, che diano l’occasione ai ragazzi anche di commettere errori, per capirli e correggerli, ma soprattutto per fare tesoro delle possibilità di comprensione che questi errori offrono.

Il lavoro di squadra
Da soli si possono imparare tante cose, non lo nego. Ma sono sempre più convinta che la matematica sia qualcosa che si impara molto meglio se si lavora con qualcun altro. È vero per noi adulti: senza il gruppo di docenti e tutor dei corsi MathUp con i quali collaboro da alcuni anni, non avrei veramente compreso tante cose. Ma è vero anche per i nostri alunni: formulare e confutare ipotesi, argomentare, verificare, descrivere… sono tutti processi che essi mettono in atto più spontaneamente, e che affinano meglio, se non lavorano da soli.

Le mani
Si dice che uno dei motivi per cui la matematica risulta tanto difficile è il fatto che sia una disciplina astratta. Penso che il problema non sia (solo) l’astrazione di per sé, ma (ancor prima) il fatto che, sempre più spesso, ai nostri alunni mancano le esperienze concrete dalle quali astrarre i concetti matematici. Sono convinta che non sarei arrivata nemmeno io a capire l’astrattissimo concetto di superficie senza vedere, toccare, costruire i miei modellini di carta, DAS e carta lucida: potrei mai pretenderlo dai miei alunni?

La scala a chiocciola
A lungo ho pensato che, in campo matematico, la conoscenza proceda più o meno come una linea retta: ogni argomento necessita di alcuni prerequisiti, senza i quali non può essere affrontato, e ogni argomento è propedeutico ad altri. Così come a lungo ho pensato che parlare di continuità tra ordini di scuola diversi significasse stabilire bene che cosa gli alunni devono sapere quando escono dalla scuola primaria per poter affrontare la secondaria e stabilire bene che cosa essi devono sapere quando escono dalla secondaria di primo grado per affrontare quella di secondo grado.
Forse in tutto questo non c’è nulla di veramente sbagliato, ma sicuramente manca qualcosa di fondamentale. Per comprendere a fondo un concetto matematico occorre tornarci su più e più volte, guardarlo da punti di vista diversi e ritrovarlo in contesti diversi: la strada dell’apprendimento finisce con l’assomigliare più ad una spirale, che ad una linea retta.
Per capire che la superficie non ha spessore, non mi è bastato sentirmelo dire alla scuola elementare; ho dovuto tornarci su durante la scuola secondaria, e all’università, e poi di nuovo adesso da insegnante: solo salendo ogni volta un po’ più in alto su quella scala a chiocciola che è l’apprendimento della matematica ho potuto guardare le cose un po’ più in profondità.

                                       Una spirale. Foto di Matteo Boselli

Sofia Sabatti

Note

[1] In realtà tutte le sculture che “richiamano” un nastro di Möbius sono dei tori: ad esempio quella di Norberto Marchi a Cantù, quella di Max Bill presso il Museo Mercedes-Benz di Stoccarda, quella di Josep Canal a Barcellona, quella che si trova in Lange Reihe 8 a Colonia…

[2] Quando si parla di superfici, si può dare un senso alle espressioni “sopra” e “sotto” solo se si pensano le superfici in questione immerse in un certo ambiente. Per tornare al nostro esempio: è vero che posso immaginare di stendere della pittura gialla da una parte della superficie cilindrica (e non dall’altra parte), ma questa pittura che stendo finisce con l’essere nello spazio in cui la superficie è immersa (i punti gialli non sono tanto punti della superficie, quanto punti dello spazio in cui essa sta). L’espressione “la superficie cilindrica ha due facce” (che per anni ho usato) è proprio brutta, perché la parola “facce” sta normalmente ad indicare parti diverse di una superficie e non qualcosa che va oltre la superficie stessa. Meglio dire “la superficie cilindrica è bilatera”, ma ancora non basta: la superficie cilindrica di per sé non è bilatera né monolatera. Quello che dovremmo allora dire è che la superficie cilindrica, immersa in \(\mathbf{R}^3\), è bilatera.
Analogamente: l’espressione “il nastro di Möbius ha una sola faccia” (che per anni ho usato) non dice nulla; e l’espressione “il nastro di Möbius è monolatero” è vera solo se specifichiamo che lo pensiamo immerso in \(\mathbf{R}^3\).

Una doppia foresta immagine di Filippo Favale. Un nastro cilindrico, immerso in \(\mathbf{R}^3\), è una superficie bilatera. Gli alberi delle foreste di questa immagine sono un buon modo per rappresentare il vettore normale alla superficie e la possibilità di scegliere coerentemente su questo vettore un verso (in verde) e il suo opposto (in rosso).	Una foresta immagine di Filippo Favale. Un nastro di Möbius, immerso in \(\mathbf{R}^3\), è una superficie monolatera. Gli alberi della foresta di questa immagine rappresentano il vettore normale alla superficie ed evidenziano che non è possibile scegliere coerentemente un verso su questo vettore: si passa con continuità dagli alberi verdi a quelli rossi.

Per capire come possano esserci caratteristiche delle superfici non intrinseche alle superfici stesse, ma che dipendono dall’ambiente in cui esse sono immerse, personalmente ho dovuto “scendere di dimensione”; senza questo passaggio non credo che sarei riuscita a capire che cosa significhi pensare ad una superficie immersa in uno spazio che sia diverso dall’ordinario \(\mathbf{R}^3\). Se una circonferenza è immersa su un piano o su un toro, si può scegliere coerentemente sul vettore normale alla curva un verso (in verde) e il suo opposto (in rosso). Ma si trovano (curve topologicamente equivalenti a) circonferenze immerse in un nastro di Möbius, per le quali non è possibile scegliere in maniera coerente un verso del vettore normale alla curva.

		La circonferenza è bilatera sia se la penso immersa in un piano, sia se la penso immersa in un toro: in entrambi i casi, si può scegliere in maniera coerente uno dei due possibili versi del vettore normale alla curva.
		Ma la stessa curva (una circonferenza) immersa in una superficie diversa (il nastro di Möbius) può essere monolatera: può cioè non essere possibile scegliere in maniera coerente un verso del vettore normale alla curva.

Roberto Natalini

Roberto Natalini [coordinatore del sito] Matematico applicato. Dirigo l’Istituto per le Applicazioni del Calcolo del Cnr e faccio comunicazione con MaddMaths! e Comics&Science.