Presentiamo qui una tesina sulla la matematizzazione di un gioco, scritta da Francesco Ferrari, del Liceo Scientifico M. Curie di Tradate, allievo della Prof.ssa Francesca E. Magni, a partire da una proposta di Corrado Falcolini dell’Università di Roma Tre. Un gioco che apparentemente potrebbe non aver nulla a che fare con la matematica; una branca di questa disciplina è tuttavia in grado di descrivere e semplificare la soluzione del gioco.
di Francesco Ferrari – V AS – Liceo Scientifico M. Curie Tradate
PRESENTAZIONE DEL GIOCO [1 ]Falcolini C., Gioco 10×10, www.mat.uniroma3.it/users/falco/pls/ret10x10.doc
Il gioco 10×10 consiste nel riempire una tabella quadrata, il cui lato è lungo 10 caselle, con i numeri da 1 a 100 rispettando le seguenti regole:
- il numero 1 può essere posizionato a piacimento
- il numero successivo può essere posizionato in posizione lineare rispetto al precedente, se tra i due c’è uno spazio di due caselle, oppure diagonalmente lasciando uno spazio di una casella
Un esempio: posizionando il numero 1 come nella figura sottostante, il numero 2 può essere posizionato linearmente rispetto ad esso (nelle caselle con il cerchio) o diagonalmente (nelle caselle con il quadrato).
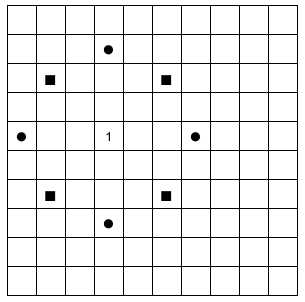
Provando ad inserire numeri senza un metodo preciso si nota che non è difficile arrivare a numeri discretamente alti, ma è molto complicato arrivare al 100.
Lo scopo di questo articolo è matematizzare il problema, ovvero cercare di descriverlo, comprenderlo e risolverlo con metodo matematico. Naturalmente è possibile trovare varianti del gioco cambiando le regole o le tabelle: si discuterà di questo nel corso dell’articolo.
Il gioco, apparentemente facile, si rivela molto complesso se studiato matematicamente.
INIZIO DEL LAVORO
Per prima cosa sono state matematizzate le regole, descrivendole in modo più preciso:
- il numero 1 può essere posizionato a piacimento in un quadrato della tabella
- ogni altro numero deve essere posizionato in una casella il cui centro disti di 3 o $$\sqrt{8}$$ dal centro della casella che contiene il numero precedente, considerando il lato di una casella lungo 1
- lo scopo del gioco è riempire la tabella
Dopo aver provato a completare qualche tabella senza alcun metodo specifico, ho deciso di provare a completare tabelle quadrate più piccole (una delle possibili varianti del gioco).
Per una tabella $$1\times 1$$ è banale capire che c’è una sola soluzione.
![]()
Per una tabella 2×2 non esistono soluzioni: infatti non è possibile eseguire mosse per qualunque posizione iniziale scelta.

Non esiste infatti nessuna casella che soddisfi le regole poste.
Lo stesso discorso vale per una tabella 3×3: dalle caselle evidenziate non è possibile eseguire alcuna mossa, perciò quelle caselle non possono neanche essere raggiunte. Infatti ciò che lega due numeri successivi è solo la distanza, quindi è possibile ripercorrere i numeri in ordine decrescente con le stesse regole.
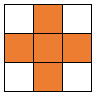
Anche la tabella 4×4 è impossibile da completare. Dimostrazione:
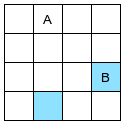
Da A, si può scegliere una delle due caselle azzurre. In questo caso ho scelto la casella in diagonale. A questo punto il percorso da seguire è obbligato, poiché da B l’unica possibilità mi porta in C, da cui si può andare solo in D, e così via fino a giungere in H, dove non si hanno più possibilità di movimento. Dato che H occupa l’altra casella raggiungibile da A, queste otto caselle formano un percorso chiuso: non è possibile completare la tabella, perché da queste caselle non ci sono altre mosse disponibili (e per questo non possono nemmeno essere raggiunte, come già spiegato).
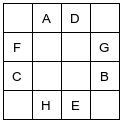
Si sarebbe potuto fare la stessa osservazione partendo da una qualunque di queste otto caselle.
LE TABELLE 5×5
Le tabelle con cinque quadrati per lato saranno trattate in un discorso a parte, perché più complesse da analizzare e, soprattutto, perché sono effettivamente risolvibili.
Dopo svariati tentativi casuali, ho trovato due soluzioni:

Dopo averle confrontate, ho notato come i numeri siano posizionati in modo molto simile: non nella stessa esatta posizione, ma nello stesso gruppo di caselle (es. il 2 esterno, il 12 negli angoli, ecc…). Ho quindi pensato all’esistenza di “gruppi di soluzioni”, cioè soluzioni accomunate dalla posizione dei numeri nella tabella. In questo caso, il gruppo di soluzioni si sarebbe potuto indicare così (in azzurro le modifiche per un secondo gruppo di soluzioni e in rosso per un terzo, molto simili al primo):

dove a ∈ {1;12;14;25} v {1;12;14;23} v {3;12;14;23}
b ∈ {2;4;6;7;9;11;15;17;19;20;22;24}
c ∈ {3;10;16;23} v {3;10;16;25} v {1;10;16;25}
d ∈ {5;8;18;21}
Seguendo le regole del gioco e riempiendo la tabella secondo le indicazioni fornite dal gruppo di soluzioni, si viene guidati alla soluzione.
Dato che la relazione tra caselle contenenti numeri successivi è solo la distanza, un percorso da 1 a 25 può essere ripercorso da 25 a 1 seguendo le stesse regole. Allo stesso modo, se si riesce a scrivere i numeri da 1 a 13, con il 13 al centro e lasciando le caselle simmetriche rispetto al centro una libera e una occupata, i restanti numeri possono essere inseriti compiendo il percorso simmetrico [2 ]Favero G., http://www.vialattea.net/esperti/php/risposta.php?num=2288. Questo è un modo abbastanza efficace di riempire tabelle 5×5, dato che, come spiegato prima, si può partire dal 13 centrale e andare fino all’1, per poi completare con i restanti numeri.
Trovate queste soluzioni alle tabelle 5×5, ho proseguito il lavoro in due direzioni: trovare tutte le soluzioni possibili alle tabelle (ad es. scegliendo la posizione iniziale o finale) e risolvere una tabella 10×10: infatti questa può essere vista come quattro tabelle 5×5, facilitando di molto la risoluzione.
Dal gruppo di soluzioni indicato in rosso si ottiene una tabella in cui l’1 e il 25 sono collegati tra loro con una singola mossa: ciò significa che la soluzione è ciclica, e quindi è possibile partire da una qualunque casella e completare la tabella 5×5. Infatti, partendo dalla soluzione ciclica, si può sostituire ogni numero n con (n+k)(mod 25)+1, con k numero intero a piacere, ed ottenere un’altra soluzione con inizio e fine diversi da quelli di partenza.
LA TABELLA 10×10
Utilizzando la tabella 5×5 risolta con la classe di soluzioni precedentemente indicata in rosso, si ottiene una tabella con l’1 e il 25 in caselle con un vertice in comune con la casella centrale, disposte cioè diagonalmente rispetto ad essa. Accostando quattro di queste tabelle, è possibile collegare il 25 di una tabella con l’1 della successiva, dopo aver ruotato opportunamente la tabella: a questo punto è sufficiente riscrivere l’1 della seconda tabella come 26, il 2 come 27, ecc… fino ad arrivare al 100. In termini matematici, se si assegna ad ogni tabella un numero, partendo ad esempio da in alto a sinistra e procedendo in senso orario, ad ogni numero va sommato 25(n-1), dove n indica il numero della tabella (da 1 a 4). La soluzione da riportare usando la simmetria è indicata nella tabella 1.
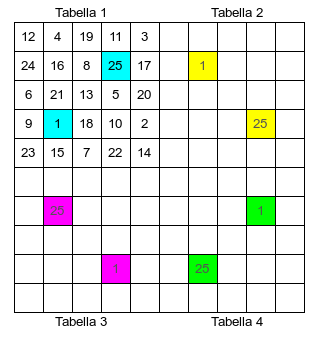
La simmetria nelle tabelle: come già affermato, da una tabella è possibile ricavare altre tabelle simmetriche. Esistono tre tipi di simmetrie:
1) Si può usare la riga o la colonna centrale o una delle due diagonali come asse, scambiando di posto i numeri che si trovano in caselle che rispettano le seguenti condizioni:
-i loro centri si possono unire con una linea perpendicolare all’asse scelto
-le distanze tra i loro centri e l’asse sono congruenti
2) Si può riscrivere la tabella al contrario, scrivendo 1 al posto di 25, 2 al posto di 24, e così via. In termini matematici, ogni numero n è sostituito da 26-n
3) Si può usare la casella centrale come punto di simmetria, scambiando di posto numeri che si trovano in caselle che presentano le seguenti proprietà:
-i loro centri si possono unire con una linea che passi dal centro dalla casella centrale
-le distanze tra i loro centri e il centro dalla casella centrale sono congruenti
La simmetria 3 corrisponde a due successiva simmetrie 1, una con asse verticale e una con asse orizzontale. Nel caso di una tabella risolta usando il metodo della casella simmetrica libera, le simmetrie 2 e 3 sono equivalenti.
Inoltre, si possono ottenere tabelle equivalenti a quella di partenza effettuando rotazioni con centro corrispondente alla casella centrale (è come guardare la stessa tabella ruotando la testa), infatti la rotazione non cambia le distanze tra caselle.
Una tra le soluzioni complete della tabella 10×10 è la seguente: partendo dalla soluzione 5×5 appena proposta, dalla tabella 1 alla 2 è stata eseguita una simmetria assiale orizzontale, dalla 2 alla 3 una simmetria assiale verticale, dalla 3 alla 4 un’altra assiale orizzontale. La soluzione è anche ciclica, cioè è possibile passare dal 100 all’1.
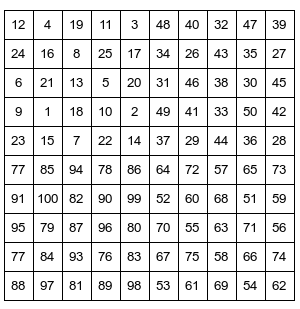
La soluzione (o meglio una delle soluzioni) è stata trovata, ma lo studio del gioco può proseguire per trovare altre soluzioni o per analizzare varianti del gioco.
Si noti che anche questa soluzione della tabella 10×10 è ciclica, perciò vale il ragionamento fatto precedentemente per la tabella 5×5: esiste almeno una soluzione per ogni casella iniziale. Per trovare una soluzione per ogni casella iniziale partendo dalla tabella soprastante, si può sostituire ogni numero n con (n+k)(mod 100)+1.
ALTRE SOLUZIONI PER LE 5×5: I GRAFI
Per cercare altre soluzioni alle tabelle 5×5, in modo da poterle risolvere per qualunque posizione di partenza, inizialmente ho usato la tecnica della casella simmetrica libera, esplorando tutte le possibilità con un grafico ad albero. Posizionando il 13 in centro e proseguendo all’indietro, ho cercato tutti i modi di riempire la tabella da 1 a 13 lasciando la casella simmetrica rispetto al centro libera. Non sono state trovate soluzioni diverse da quelle già esaminate, e così la tecnica della casella simmetrica è stata abbandonata.
Per trovare altre soluzioni, si è dovuto ricorrere alla teoria dei grafi [1], il cui collegamento con il gioco 10×10 risulta molto interessante. La teoria dei grafi è la branca della matematica che studia i grafi: questi sono strutture matematiche discrete (ovvero che non richiedono la proprietà della continuità; la maggior parte delle strutture matematiche discrete sono insiemi). Un grafo viene definito come una coppia ordinata G = (V, E) di insiemi, dove V è l’insieme dei nodi (o vertici) del grafo ed E è l’insieme di lati o archi. Due vertici u,v connessi da un arco detto (u,v) si dicono estremi dell’arco, mentre l’arco è detto incidente ai vertici che ha per estremi. Un vertice v ha un grado d(v), che è il numero di archi incidenti ad esso [3 ]Bonaccorsi S., Teoria dei grafi e applicazioni, http://www.science.unitn.it/probab/Mathmodels/article-grafi-noslide.pdf, [4 ]Amato A., Gionfriddo M., Ragusa G., Appunti di teoria dei grafi, http://www.spazioblog.it/uploads/g/giorgioragusa/212322.pdf, pp. 13-15.
Per comprendere l’utilizzo della teoria dei grafi, è utile considerare come esempio il problema da cui questa branca della matematica è nata: il problema dei ponti di Königsberg. Il fiume Pregel attraversava la città di Königsberg, in Prussia (oggi è la città russa Kaliningrad), e, dividendosi, dà origine a due isole nel centro della città. Per gli abitanti era diventata una sfida, durante le passeggiate, cercare di attraversare tutti i 7 ponti sul fiume una e una sola volta tornando al punto di partenza.
Nel 1735 Eulero si occupò del problema dimostrando che è impossibile compiere un percorso del genere: per farlo disegnò ogni regione di spazio come un puntino e ogni ponte come una linea, semplificando il problema. Poi dedusse che ogni regione di spazio doveva essere collegata a un numero pari di ponti: ogni volte che si entra in quella zona, bisogna poi uscirne con un ponte diverso; il primo e l’ultimo possono fare eccezione a questa regola, ma in questo caso arrivo e partenza coincidono, perciò anche quel vertice deve avere due archi incidenti [5 ]Du Satoy M., L’enigma dei numeri primi. L’ipotesi di Riemann, il più grande mistero della matematica, Milano, Rizzoli, 2004, pp. 56, [6 ]Singh S., L’ultimo teorema di Fermat. L’avventura di un genio, di un problema matematico e dell’uomo che lo ha risolto, Milano, BUR, 1999, pp. 84-86.

Disegno dei ponti di Königsberg e grafo corrispondente.
Per il gioco 10×10, è possibile associare ogni casella a un vertice del grafo, collegando poi i nodi le cui corrispondenti caselle sono a distanza 3 o $$\sqrt{8}$$. In questo modo la soluzione è molto più semplice da trovare: è sufficiente partire da un punto qualsiasi e cercare un percorso che passi per tutti i nodi una e una sola volta. Un percorso che passi attraverso tutti i nodi una sola volta è detto cammino hamiltoniano; se la partenza coincide con l’arrivo, il percorso si dice ciclo hamiltoniano. Inoltre, un percorso che tocchi tutti gli archi di un grafo una e una sola volta è detto cammino euleriano; se la partenza coincide con l’arrivo, il percorso è detto ciclo euleriano [7 ]Casali M., Grafi euleriani e hamiltoniani, http://cdm.unimo.it/home/matematica/casali.mariarita/Grafi_euleriani-hamiltoniani.pdf.
Esistono teoremi che permettono di riconoscere alcune condizioni sufficienti ma non necessarie affinché un grafo abbia un ciclo hamiltoniano, ma si discuterà successivamente di questi, in quanto ho svolto il lavoro sui grafi senza questi teoremi.
Ho usato la teoria dei grafi anche per verificare che la tabella 4×4 è impossibile, dimostrandolo in modo più semplice (il grafo è formato due percorsi chiusi separati, è quindi impossibile completare un percorso che passi da tutti i nodi).
L’applicazione della teoria dei grafi al gioco si effettua in questo modo: a ogni casella della tabella 5×5 è stata assegnata una lettera, in modo da indicare ognuna di esse con il nodo che contiene quella lettera.

Ogni nodo è collegato ai nodi in cui è possibile spostarsi con una sola mossa: il nodo A, ad esempio, sarà collegato ai nodi D, M e P, poiché da A ci si può spostare in quelle caselle e viceversa.
Studiando le connessioni tra le caselle, il grafo risultato è questo:
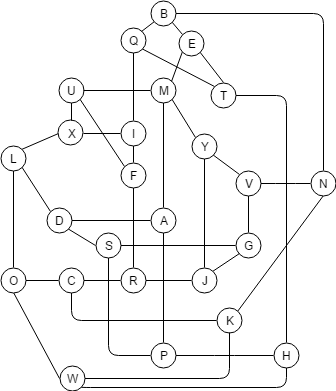
Trovando vari percorsi, ho trovato soluzioni della tabella 5×5 per qualsiasi posizione iniziale (o finale, percorrendo il grafico al contrario). Le soluzioni possono essere riassunte in sei tabelle in quanto, ad esempio, dando la soluzione con posizione iniziale in un angolo, si possono trovare quelle con posizione iniziale negli altri angoli, usando le simmetrie o la rotazione.

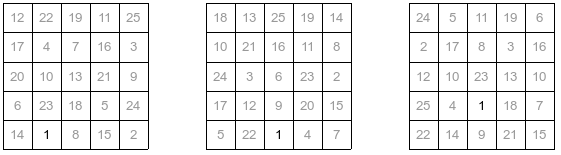
Si ricorda che queste non sono tutte le soluzioni possibili (a meno di simmetrie), ma semplicemente un esempio di soluzione per ogni posizione iniziale. Tuttavia questo permette di risolvere tabelle costruite accostando 5×5, ad esempio tabelle rettangolari, o di forme particolari (se costruite accostando adeguatamente tabelle 5×5), o ancora tabelle quadrate con lato di 5n caselle, vedi [1]: una volta date queste sei soluzioni, risulta piuttosto semplice riempire tabelle anche 50×50, o più grandi: una volta riempita la prima 5×5, si sceglie la posizione di partenza di quella successiva, che deve essere legata con una mossa all’ultimo numero della precedente, si riempie quella tabella e si procede di questo passo.
VARIANTI DEL GIOCO
Si possono studiare varianti del gioco: la prima analizzata è stata una variazione della regola che lega due caselle con numeri successivi. La mossa in questa variante è uguale a quella che fa il cavallo nel gioco degli scacchi, cioè una L con lati di due e tre caselle [1]. In termini matematici, la distanza tra caselle contenenti numeri successivi deve essere $$\sqrt{5}$$.
La tabella $$1\times 1$$ presenta una soluzione banale. Le tabelle $$2\times 2$$ e $$3\times 3$$ non presentano soluzioni possibili:
nella prima non si possono fare mosse, nella seconda la casella centrale non è raggiungibile.
La tabella $$4\times 4$$ è associata ad un grafo più complesso:
Studiando questo grafo, ho dimostrato l’impossibilità di risolverlo.
Dimostrazione: si considerino i due “gruppi” di vertici J-P-A-G e K-M-F-D
Essi hanno la stessa struttura e perciò verrà studiato solo uno dei due, ad esempio J-P-A-G. Se si arriva in J, si può proseguire in A-G, per poi continuare ma lasciare isolato P; oppure proseguire in P-G, continuare e lasciare isolato A; oppure proseguire in A-G-P o P-G-A per poi non avere più archi a disposizione. Il ragionamento si ripete identico considerando di partire da G. Partendo invece da A o P, si possono usare tutti i nodi e poi avere ancora archi disponibili (es. A-J-P-G). Quanto appena detto vale anche per il gruppo K-D-M-F. I due gruppi considerati non possono allora essere intermedi nella risoluzione del grafo, ma possono essere solo la partenza o l’arrivo. I due gruppi di arrivo e di partenza sono stati “riassunti” nei vertici G1 e G2, estremi di tutti gli archi incidenti nei nodi che raggruppano.
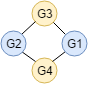
La stessa operazione si può fare per i restanti vertici, raggruppandoli in altri due vertici e ottenendo il seguente grafo.
Sapendo che bisogna partire in G1 o G2 e finire in G1 o G2, si nota che è impossibile passare da tutti i vertici: i vertici raggruppati in G3 o G4 verranno sicuramente esclusi. Il grafo iniziale non contiene allora alcun cammino hamiltoniano.
Ho quindi risolto una tabella 8×4 con il grafo corrispondente, per poi accostarne due e trovare una soluzione per una 8×8: ciò significa che il pezzo del cavallo può saltare su tutte le caselle della scacchiera senza passare due volte per la stessa. Ecco la tabella 8×4 e il relativo grafo:


(alcuni archi sono colorati per evitare confusione)
Dal grafo ho trovato la soluzione: Y-J-D-U-A’-Q-B-L-F-P-E’-N-H-W-C’-S-I-Z-K-A-R-B’-V-F’-O-ET-C -M-G-X-D’
Dato che la soluzione inizia da una casella in un angolo e arriva in una casella dalla quale si può passare direttamente all’angolo di una tabella adiacente, la soluzione può essere riportata (dopo essere stata specchiata sia in verticale sia in orizzontale) in una tabella accostata alla prima per ottenere la soluzione completa, che è anche ciclica.

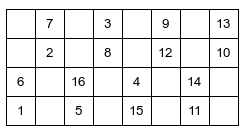
Nel riportare la soluzione nella tabella, si è notato che, nonostante sia stata trovata scegliendo un percorso casuale, è estremamente ordinata: il primo quarto di tabella riempito si presenta così:
TEOREMI RIGUARDANTI I CAMMINI HAMILTONIANI [4]
Alcuni teoremi dimostrano che un grafo è hamiltoniano se sono rispettate certe condizioni.
Il teorema di Dirac afferma che un grafo con $$n\geq 3$$ vertici è hamiltoniano se ogni vertice è di grado maggiore di $$\frac n 2$$.
Il teorema di Ore afferma che un grafo con $$n\geq 3$$ vertici è hamiltoniano se, per ogni coppia di vertici non adiacenti, la somma dei loro gradi è $$S\geq n$$. Entrambi si basano sul fatto che un grafo è hamiltoniano se ha abbastanza vertici. In nessun caso questi teoremi erano utilizzabili nei grafi qui studiati. Il teorema di Bondy-Chvátal è una generalizzazione dei due precedenti teoremi: afferma che un grafo è hamiltoniano se e solo se la sua chiusura è hamiltoniana. La chiusura di un grafo G, indicata con cl(G), si ottiene aggiungendo archi uv che collegano coppie di vertici u, v, tali che la somma dei loro gradi $$d(u)+d(v)> n$$ finché non esistono più coppie di vertici con questa proprietà.
Francesco Ferrari
Ringraziamenti. Ringrazio la professoressa Francesca E. Magni, il professor Corrado Falcolini e il professor Roberto Natalini per i suggerimenti, le correzioni e l’attenzione dedicata. I siti internet sono stati consultati l’ultima volta il 14/04/2017.
Note e riferimenti
| ⇧1 | Falcolini C., Gioco 10×10, www.mat.uniroma3.it/users/falco/pls/ret10x10.doc |
|---|---|
| ⇧2 | Favero G., http://www.vialattea.net/esperti/php/risposta.php?num=2288 |
| ⇧3 | Bonaccorsi S., Teoria dei grafi e applicazioni, http://www.science.unitn.it/probab/Mathmodels/article-grafi-noslide.pdf |
| ⇧4 | Amato A., Gionfriddo M., Ragusa G., Appunti di teoria dei grafi, http://www.spazioblog.it/uploads/g/giorgioragusa/212322.pdf, pp. 13-15 |
| ⇧5 | Du Satoy M., L’enigma dei numeri primi. L’ipotesi di Riemann, il più grande mistero della matematica, Milano, Rizzoli, 2004, pp. 56 |
| ⇧6 | Singh S., L’ultimo teorema di Fermat. L’avventura di un genio, di un problema matematico e dell’uomo che lo ha risolto, Milano, BUR, 1999, pp. 84-86 |
| ⇧7 | Casali M., Grafi euleriani e hamiltoniani, http://cdm.unimo.it/home/matematica/casali.mariarita/Grafi_euleriani-hamiltoniani.pdf |























Con un paio di amici abbiamo sviluppato un’app di questo rompicapo per Android e iOS. Ovviamente è gratuita ed è un buon modo di passare il tempo spremendosi le meningi 🙂
L’abbiamo chiamata SquareOFF !
Lascio il link se qualcuno volesse scaricarla:
Android -> https://play.google.com/store/apps/details?id=com.squareoff.squareoff
iOS -> https://apps.apple.com/us/app/square-off/id1514169653