Problemi Classici – Due triangoli

da Rudi Mathematici | 12 Novembre 2024 | Problemi, Vecchi Classici della M.R. | 1 commento

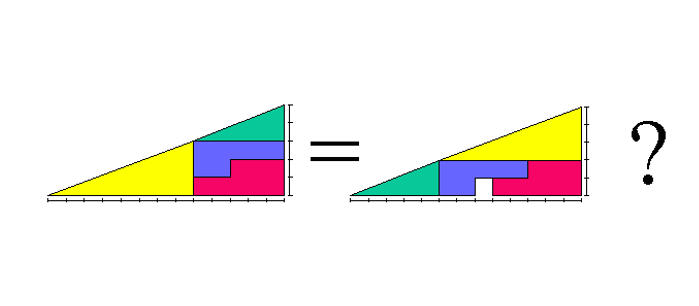
I pregi di questo famosissimo indovinello sono così tanti che è difficile elencarli tutti. È stato coniugato in decine di forme, anche con qualche significativa variazione concettuale (la più popolare in rete è probabilmente il video in cui si taglia in maniera opportuna una tavoletta di cioccolata, se ne estrae (e si mangia) un quadratino e poi si ricompone magicamente la tavoletta intera). Ma la versione riportata in figura – oltre ad avere l’impareggiabile merito di essere stato il primissimo problema presentato sulla e-zine degli autori di quest’articolo (che comunque non sono certo i creatori del problema) – ha delle doti importanti che dovrebbero essere tenute in considerazione.

La prima, ovviamente, è la totale assenza di parole nell’esposizione: questo protegge spettacolarmente dagli inganni di cui si è parlato nel paragrafo precedente, disinnescando ogni possibile trabocchetto celato dal linguaggio. I due soli caratteri tipografici sono il punto interrogativo, che sta lì a sancire che effettivamente di un quesito si tratta, e il segno dell’uguale, che però mostra proprio tutta la sua schizofrenia, perché le immagini sembrano subito contraddirlo visto che uguali le due figure non sembrano per colpa di quel quadratino mancante. Un’altra dote assai rara del quesito è che non è neppure strettamente legato alla carta: è pedissequamente onesto nel definire le dimensioni dei pezzi colorati che compongono le figure grazie alle scale orizzontali e verticali che le accompagnano, e questo suggerisce, in qualche modo, che è del tutto lecito, quasi auspicabile, procurarsi seghetti, compensato e vernici per costruire il problema con indiscutibili e del tutto reali pezzi di legno colorati. E se si decidesse di farlo, i pezzettini di legno colorato non farebbero altro che confermare l’imbarazzo del buco di una esatta unità quadrata.

Qui continua la soluzione, non leggetela se – miracolosamente – non la conoscete già e volete pensarci un po’ su.

Cliccando qui si vede la soluzione!

Il mistero si risolve in fretta se si decide di tornare innanzitutto alle scuole elementari: ogni diligente scolaretto, se incontra qualche problema nei conti dell’area di un triangolo, li rifà per sicurezza. Lui si ricorda che la formula magica recita “base per altezza diviso due”, e noi ce lo immaginiamo mentre confabula con la compagna di banco, e insieme verificano sul primo triangolo: la base è lunga 13, l’altezza 5, quindi l’area totale è 32,5. Sbuffano entrambi per quel totale con la virgola, poi si mettono a contare le aree di tutti i pezzettini: il triangolo giallo vale 12, quello verde ha area 5, e per i due pezzetti dalla forma strana basta contare: il rosso vale 8 e il blu vale 7. E quindi tutti i pezzetti assieme valgono 12+5+8+7=32, e allora i conti non tornano per nessuno dei due triangoli, perché al primo manca mezza unità quadrata mentre al secondo ne avanza mezza, se vogliamo conteggiare anche il suo buchetto. E allora? Allora, speriamo che l’insegnante, soddisfatta dell’esercizio, sia mossa a pietà e li consoli rivelando l’atroce verità: se “base per altezza diviso due” non dà l’area giusta di un triangolo, non è la formula ad essere sbagliata, è il triangolo. E infatti, i due triangoli del disegno, ahimè, non sono affatto triangoli, siamo noi che ci illudiamo che lo siano. E questa illusione la paghiamo cara, perché trattare due quadrilateri (uno concavo e uno convesso, tra l’altro) come si trattano due triangoli è errore grave. È una lezione assai dura da mandar giù, ma non c’è niente da fare: Sancio Panza non ha alcuna speranza di convincere Don Chisciotte, se Don Chisciotte è già convinto per conto suo. E non c’è inganno più potente dell’autoinganno, perché siamo abituati da tutta la vita a fidarci di noi stessi.