Mancano pochi giorni alle semifinali dei Campionati Internazionali di Giochi Matematici, l’unica gara matematica aperta anche ai professionisti. Proponiamo quindi ai lettori di Madd:Maths! un problema nello stile tipico dei giochi. Come allenamento o come stimolo a partecipare il prossimo anno.

Questo problema, e i prossimi che presenteremo, sono inediti. Problemi ideati da un giochista storico, che ha scelto l’anonimato.

Buon divertimento con

1 – Un regalo inusuale

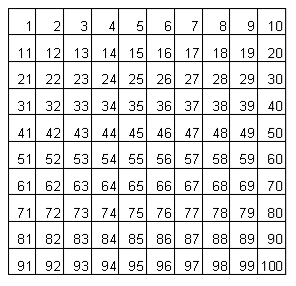
Giorgio ha ricevuto in regalo per il compleanno una scacchiera $$10\times10$$ con solo caselle bianche, numerate da 1 a 100.
Jacopo lo sfida a colorare alcune caselle di nero in maniera che l’opera finita goda delle seguenti proprietà:
a) ogni quadrupla di caselle all’incrocio di due righe e due colonne ha almeno una casella bianca;
b) se si colorasse di nero una qualunque casella ancora bianca, la proprietà a) non sarebbe più valida;
c) il numero di caselle colorate è il minimo possibile.
In quanti modi diversi Giorgio potrà colorare la scacchiera?

N.B. Le due righe e le due colonne della proprietà a) non sono necessariamente adiacenti: una quadrupla di caselle può essere 1, 2, 11, 12, ma anche 34, 37, 54, 57 (vedi figura).

La soluzione alla prossima puntata!

L’anonimo giochista

Alberto Saracco