Un team dell’Università di Ginevra, in collaborazione con l’Università CY Cergy di Parigi e l’Università della Borgogna ha analizzato i disegni realizzati da bambini e adulti durante la risoluzione di semplici problemi di matematica scoprendo che, a prescindere dall’età, le strategie di calcolo più efficaci sono associate a determinate tipologie di disegno. Questi risultati, pubblicati sulla rivista Memory & Cognition, aprono nuove prospettive per l’insegnamento della matematica.
In matematica, a scuola, si incontrano spesso piccoli problemi legati a situazioni concrete di tutti i giorni. Gli alunni, per esempio, a volte devono sommare determinate quantità di farina per realizzare una ricetta o sottrarre somme di denaro per scoprire cosa è rimasto nel portafoglio dopo la spesa. Sono così portati a tradurre frasi in procedure algoritmiche per arrivare alla soluzione. Questa traduzione delle parole in strategie risolutive prevede una fase di rappresentazione mentale delle informazioni matematiche (numeri o l’operazione aritmetica da eseguire) e di informazioni non matematiche (come il contesto del problema). Avere un’idea più chiara di queste rappresentazioni mentali consentirebbe di comprendere meglio la scelta delle strategie di calcolo.
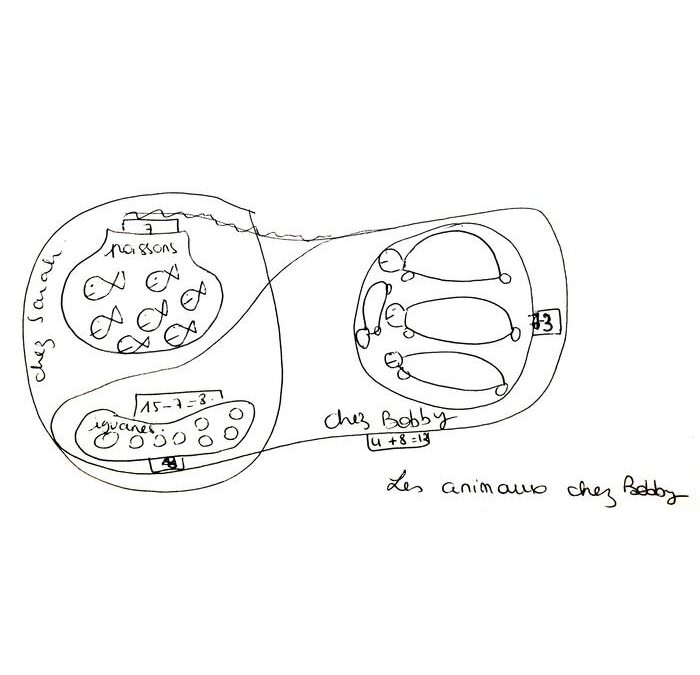
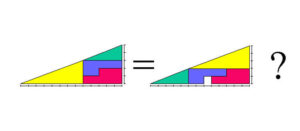
Gli scienziati hanno condotto uno studio con bambini di 10 anni e adulti chiedendo loro di risolvere semplici problemi nel minor numero possibile di passaggi. Ai partecipanti è stato poi chiesto di produrre un disegno o un diagramma che spiegasse la loro strategia di risoluzione. Il contesto di alcuni problemi faceva riferimento alle proprietà cardinali dei numeri (la quantità di elementi in un insieme) quello di altri alle loro proprietà ordinali (la loro posizione in un elenco ordinato).
“La nostra ipotesi era che problemi cardinali ispirassero i disegni cardinali, cioè diagrammi con singoli elementi identici, come croci o cerchi, o con sovrapposizioni di elementi in insiemi o sottoinsiemi. Allo stesso modo, abbiamo ipotizzato che i problemi ordinali avrebbero portato a rappresentazioni ordinali, cioè diagrammi con assi, graduazioni o intervalli – e che questi disegni ordinali avrebbero riflettuto le loro rappresentazioni mentali, il che avrebbe indicato un maggiore successo nell’identificare la strategia di soluzione in un unico passaggio” spiega Hippolyte Gros, dell’UNIGE, primo autore dello studio.
Queste ipotesi sono state confermate analizzando i disegni dei 52 adulti e 59 bambini. “Abbiamo dimostrato che, indipendentemente dalla loro esperienza, l’uso delle strategie dei partecipanti dipendeva dalla loro rappresentazione del problema e che questa è influenzata dalle informazioni non matematiche contenute nella formulazione del problema, come rivelato dai loro disegni”, spiega Emmanuel Sander, dell’UNIGE, altro autore dell’articolo. “Il nostro studio mostra anche che, anche dopo anni di esperienza nella risoluzione di addizioni e sottrazioni, la differenza tra problemi cardinali e ordinali rimane molto marcata. La maggior parte dei partecipanti è stata in grado di risolvere solo problemi del secondo tipo in un unico passaggio”.
Dal punto di vista pedagogico, questo risultato suggerisce che la presenza di caratteristiche specifiche nel disegno di uno studente può o meno indicare che la sua rappresentazione del problema è quella più efficiente per soddisfare le istruzioni.