La sensazione di colore è frutto di una lunga evoluzione e la sua modellizzazione matematica, completa o parziale, rimane ancora un problema aperto. Edoardo Provenzi, professore all’Université de Bordeaux, ci guida in un sorprendente percorso, lungo più di tre secoli, ricostruendo le tappe fondamentali dello studio matematico del colore, terminando con un racconto del suo particolare cammino scientifico. Le puntate precedenti le trovate su questa pagina.
Nei tre articoli precedenti abbiamo visto come eminenti scienziati abbiano messo l’accento sulle proprietà geometriche e algebriche soddisfatte dai colori percepiti. Schrödinger compendiò le più importanti caratteristiche algebrico-geometriche in un modello matematicamente coeso ed elegante. Era il 1920 e la fisica teorica era all’apice del suo successo, con le neonate meccanica quantistica e relatività che stavano sconvolgendo ogni fondamento scientifico pregresso. Tutto sembrava pronto per un salto nell’astrazione più profonda anche per quanto riguarda lo studio del colore…ma le esigenze industriali avevano in serbo un’evoluzione diversa per la teoria del colore…
La CIE: “what is and what should never be” (ciò che è e ciò che non dovrebbe mai essere)
La CIE, acronimo di “Commission Internationale de l’Éclairage” (commissione internazionale dell’illuminazione), fondata a Berlino nel 1913 ed ora basata a Vienna, è considerata “l’autorità internazionale sulla luce, l’illuminazione e la colorimetria”. Come vedremo a breve, questa definizione è quantomeno immeritata, almeno da un punto di vista scientifico, il ché spiega il titolo scelto per presentare la CIE, mutuato da una caustica canzone del secondo album-capolavoro dei Led Zeppelin.
La CIE, molto più interessata ad applicazioni tecnologiche del colore piuttosto che ad un suo studio scientifico (seppure, idealmente, i due interessi dovrebbero andare di pari passo…), rinuncia all’analisi matematicamente rigorosa degli anni precedenti e decide di dirigersi verso uno studio che mescola fisica, biologia e percezione in un modo caotico ed ontologicamente indifendibile. Nel 1931, sulla base di esperimenti di confronto del colore condotti da W.D. Wright (1928) e J. Guild (1931) con, rispettivamente, ben 7 e, addirittura, 10 osservatori umani…la CIE definisce l’ “osservatore colorimetrico standard” (dai dati di 17 persone…) e costruisce gli spazi di colore chiamati RGB e XYZ che oggi tutti usiamo inconsapevolmente ogni volta che guardiamo uno schermo digitale.
Naturalmente, il lettore potrebbe pensare che la resa dei colori degli schermi digitali “non è così male”…ed avrebbe totalmente ragione! Ma questo è dovuto al fatto che la tecnologia degli schermi si è dovuta adattare agli spazi della CIE, e lo ha fatto in modo egregio. Tuttavia, è estremamente probabile che una modellizzazione matematica più opportuna degli spazi di colore potrebbe portare ad una tecnologia più semplice, quindi meno costosa ed inquinante. Inoltre, i meccanismi di compressione delle immagini e, soprattutto, dei video, potrebbero essere estremamente più efficaci, con un risparmio energetico enorme per il nostro pianeta (il traffico di dati su internet generato dalla condivisione di immagini e video è già, e sarà sempre di più, una drammatica causa di inquinamento). Questa affermazione deriva dal fatto che il nostro sistema visivo ha una capacità di compressione enormemente maggiore di quella degli algoritmi attualmente in uso.
Il settore nel quale la CIE ha dato, purtroppo, il peggio di sé è sicuramente la colorimetria propriamente detta, ovvero lo studio della metrica del colore, quella che stabilisce quanto due colori siano percettivamente dissimili. La CIE ha infatti insistito, in un modo completamente arbitrario, su una metrica Euclidea, quella che tutti usiamo “inconsciamente” e che stabilisce che la distanza più corta tra due punti dello spazio è quella del segmento dell’unica retta che li congiunge. In matematica esistono molte altre metriche ed il fatto che quella Euclidea sia la più utilizzata “nella vita comune” non significa che sia quella adeguata per ogni situazione.
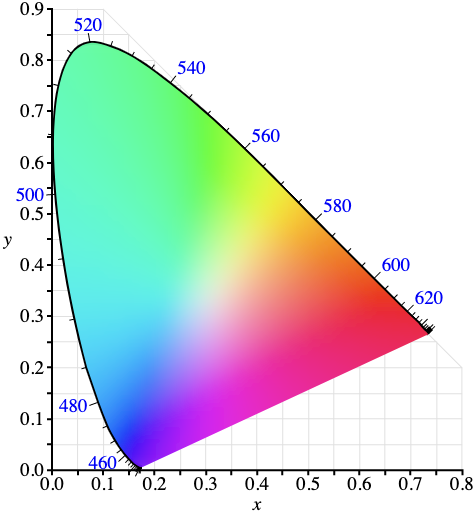
L’indizio più flagrante del fatto che la metrica che descrive la distanza percettiva tra colori non sia Euclidea lo diede David MacAdam già nel 1942. Per capire di cosa si tratta occorre introdurre il cosiddetto “diagramma di cromaticità” della CIE, una sorta di proiezione bidimensionale dello spazio tridimensionale dei colori, che è raffigurato nell’immagine a sinistra della figura sottostante.
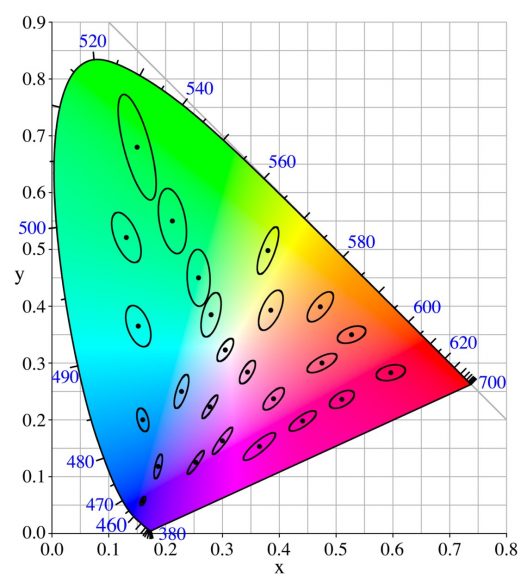
Ogni colore di questo diagramma è associato a una coppia di coordinate, indicata con (x,y). MacAdam mostrò ad un campione di osservatori il colore corrispondente ad una coppia (x,y) e poi variò poco a poco il colore fino a quando gli osservatori dichiaravano di aver percepito una variazione rispetto al colore iniziale, indicata solitamente con JND, acronimo dell’inglese “Just Noticeable Difference” (differenza appena percepibile). Ebbene, se la distanza percettiva tra colori fosse Euclidea, le coppie relative alle JND dovrebbero formare un cerchio con centro dato dalla coppia iniziale (x,y). Invece, come si vede dall’immagine di destra della figura precedente, non si tratta di cerchi ma di ellissi e, per di più, con dimensioni estremamente diverse e posizionate in modo per niente omogeneo nel diagramma di cromaticità.
Nonostante questa evidenza, e parecchie altre, la CIE ha atteso fino al 1976 (!!) per proporre una soluzione al problema, cruciale, della determinazione di una metrica percettiva. Il risultato fu, per utilizzare un eufemismo, quantomeno deludente: la CIE decise di mantenere testardamente una metrica Euclidea col compromesso di modificare le coordinate cromatiche in un modo euristico ed esclusivamente sulla base dell’interpolazione sperimentale. La conseguenza è un modello, chiamato CIELab, “aggiustato” con parametri che arrivano fino alla quarta cifra decimale, con buona pace delle cifre significative e dell’analisi di propagazione degli errori che chiunque può studiare al primo o secondo anno di scuola superiore.
Jan Koenderink, noto e rispettato studioso del colore, ha utilizzato le seguenti parole per descrivere il modello CIELab: “l’attuale standard industriale, lo spazio CIELab, è un misto imbarazzante di colorimetria e definizioni arbitrarie […] pieno di numeri magici e funzioni ad-hoc. Tuttavia, abbastanza comunemente, la gente confonde questo con la scienza!”.
Le dure, ma condivisibilissime, parole di Koenderink mostrano quanto un modello mal fatto da un punto di vista matematico possa irritare chi tenta di mettere ordine nel caos, per citare quanto detto in precedenza su Schrödinger. Va detto in modo molto chiaro che la modelizzazione matematicamente rigorosa di qualsiasi fenomeno richiede solitamente molto più tempo di una soluzione euristica ed approssimativa, ma quando la teoria matematica è finalmente formulata i vantaggi derivanti da quest’ultima ripagano di gran lunga l’attesa. Ciò, naturalmente, non vuol dire che non si debbano produrre modelli approssimati mentre si attende la soluzione rigorosa ad un problema, altrimenti molta della tecnologia che abbiamo usato in passato e che usiamo tutt’oggi non esisterebbe, ma vuol dire che occorre avere l’onestà intellettuale di dichiarare che un modello è approssimato e di sostenere anche la ricerca “pura”, che si pone domande non necessariamente legate a delle finalità pratiche ed immediate e che, grazie a questa libertà, spesso scopre che la soluzione ottimale di un problema è collegata all’uso di tecniche che potrebbero sembrare non avere alcuna relazione col problema affrontato!
Tornando alla metrica percettiva per distinguere tra colori, è importante osservare come tutti, ma proprio tutti, i ricercatori che si sono dedicati a questo tema nella seconda parte del ventesimo secolo hanno trovato risultati concordanti verso un solo tipo di metrica alternativo a quella Euclidea: si tratta della cosiddetta metrica “iperbolica”. Questo tipo di metrica appare in modo naturale durante lo studio di spazi con una geometria “curva” come quella del cosiddetto “iperboloide a due falde“ rappresentato nella figura qui sotto, nel quale la minima distanza tra due punti di una stessa falda non è rappresentata dalla lunghezza di un segmento di retta, ma da quella di un arco d’iperbole.
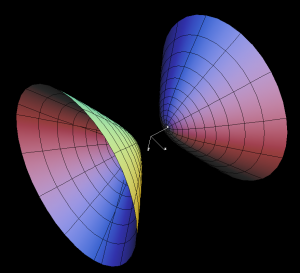
Non credete a chi vi dice che questo concetto è intuitivo, non lo è per niente e, a riprova di ciò, si pensi che persino il grande Gauss, che aveva capito probabilmente per primo l’importanza di questo tipo di geometrie oggi chiamate “non-Euclidee”, ebbe paura a pubblicare anche solo un articolo a riguardo per “non far arrabbiare gli antichi greci” (uproar the Boetians).
Fare una selezione degli eccellenti lavori che discutono l’importanza delle metriche iperboliche in riferimento alla percezione del colore non è semplice, la scelta è ricaduta su due modelli: quelli di Yilmaz e di Resnikoff, che affronteremo nella quinta parte di questa serie.
Edoardo Provenzi
#Fine quarta parte




















È verissimo Rossana, le consiglio anche questo sito:
https://www.universityaffairs.ca/features/feature-article/the-slow-science-movement/
Si è giunti così ad uno stop per la ricerca, l’industria viaggia con tempi ed obiettivi differenti. Questa logica utilitaristica con l’immediato utilizzo ad ogni costo, anche in via approssimata, ci ha portati, non solo, agli attuali problemi ambientali ma anche ad una diffusa superficialità del pensiero critico. Il cammino della scienza, anche se più lungo, probabilmente, avrebbe trovato soluzioni più adeguate, più rigorose e soprattutto più dignitose. Il luogo comune dell’industria ci percepisce come banali e passivi fruitori di oggetti, piuttosto che come pensatori, creatori e realizzatori di idee.