In un recente studio è stata presentata la ricetta matematica per ottenere la giusta cremosità nella cacio e pepe. Ce ne parla Marco Menale.

Domenica a pranzo. Sei ai fornelli e vuoi deliziare gli ospiti con una bella cacio e pepe. Ovviamente, con i tonnarelli. L’acqua è sul fuoco, il sale è a portata di mano e il pecorino è grattugiato. Hai pure preparato la boule per quella fantastica cremina che è, poi, un po’ il cuore di questo piatto. Ma quanta acqua mettere? E Come regolarsi con il formaggio? Eh sì, cominciano quelle domande perché se la salsa non è cremosa non è cacio e pepe. Un recente studio comparso su arxiv ne ha rivelati i segreti matematici.

L’articolo è “Phase behavior of Cacio and Pepe sauce”, lavoro di un gruppo di fisici [G. Bartolucci, D. M. Busiello, M. Ciarchi, A. Corticelli, I. Di Terlizzi, F. Olmeda, D. Revignas, e V. M. Schimmenti] di diverse università europee, tra cui il Dipartimento di Fisica e Astronomia “Galileo Galilei” dell’Università di Padova. Ispirati da un video presente su YouTube, gli autori usano meccanica statistica e teoria delle transizioni di fase per descrivere una perfetta cacio e pepe.

Partiamo dalla difficoltà principale di questo piatto: appunto, la crema! La si ottiene mescolando l’acqua ricca di amido con il formaggio grattugiato. La presenza di amido nella giusta quantità aumenta la stabilità del composto. Tuttavia, se l’acqua è troppo calda, le proteine del formaggio possono denaturarsi e formare grumi, che si separano dall’acqua, compromettendo la buona riuscita. Inoltre, l’aggregazione delle proteine dipende dalla concentrazione di formaggio, acqua e amido: senza amido, i grumi si formano già intorno ai $65° C$.

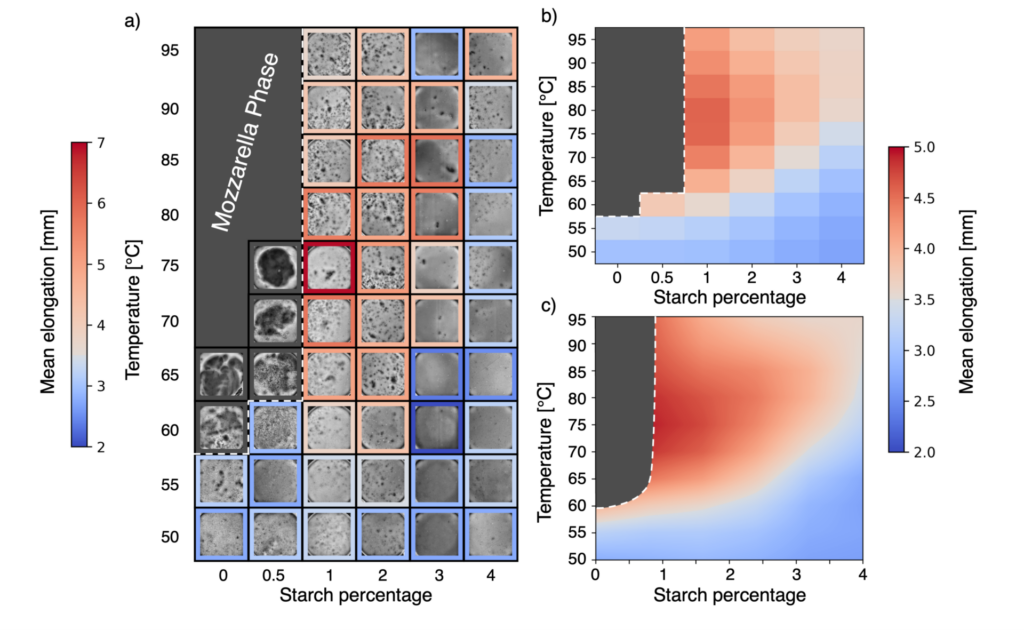
Intorno a questo problema gli autori dell’articolo spiegano con la matematica (anzi, la fisica-matematica) come evitare la formazione dei grumi e ottenere una cacio e pepe cremosa. Studiano e modellano, con esperimenti ed equazioni, il comportamento di fase della soluzione composta da acqua, amido e formaggio, ossia la base della crema. Analizzano in modo sistematico il ruolo di ciascuno di questi tre componenti, evidenziando come ogni elemento influisca sulla stabilità e sulla consistenza del risultato finale. L’obiettivo è evitare la formazione dei grumi, con il rischio della “fase mozzarella”. Quest’ultima si verifica quando le condizioni di temperatura e concentrazione non sono bilanciate, così da causare l’aggregazione massiva delle proteine del formaggio, compromettendo la consistenza con enormi grumi.  L’intero processo è descritto, con il linguaggio della fisica statistica, come una transizione di fase liquido-solido.

Ma, a livello matematico? Per descrivere quantitativamente la stabilità del composto, che si spera diventi crema, gli autori introducono una funzione di energia libera del sistema e ne discutono le sue proprietà con opportuni parametri.

Clicca qui per saperne di più

La scrittura del modello matematica si base su una densità a energia libera, ottenuta considerano le proteine del formaggio e il solvente comprensivo di acqua, amido, sale e lipidi costituenti il formaggio stesso. Gli autori introducono $\phi$ e $\phi_s$, rispettivamente, per la frazione delle proteine e del solvente. Dalla conservazione segue

$$\phi + \phi_s = 1.$$

Se entrambe le componenti hanno densità quasi uguali, il diagramma di fase della miscela, in termini delle frazioni delle loro componenti, è ottenuto con la seguente densità a energia libera:

$$f = \frac{k_B T}{\nu} \left[ \frac{\phi}{n} \ln \phi + (1 – \phi) \ln (1 – \phi) + \chi \phi (1 – \phi) \right],$$

dove $\nu$ è la massa molecolare di riferimento, $n$ la dimensione relativa delle proteine del formaggio rispetto alle altre componenti in soluzione e $\chi$ il parametro di interazione tra le componenti. Per valutare il comportamento di fase della miscela, si considera il potenziale chimico di scambio

$$\mu = \nu \frac{\partial f}{\partial \phi}$$

e la pressione osmotica

$$\Pi = -f + \phi \frac{\partial f}{\partial \phi}.$$

Le condizioni affinché due fasi, indicate come $\mathrm{I}$ e $\mathrm{II}$, coesistano stabilmente sono

$$\mu^{\mathrm{I}} = \mu^{\mathrm{II}}, \quad \Pi^{\mathrm{I}} = \Pi^{\mathrm{II}}.$$

Queste equazioni devono essere risolte simultaneamente a ogni temperatura per determinare la frazione di proteine nelle fasi di coesistenza, $\phi^{\mathrm{I}}$ e $\phi^{\mathrm{II}}$. A temperature leggermente al di sopra dei $60°C$, le due soluzioni collassano, cioè $\phi^I = \phi^{II}$. A questo punto il tutto sta nel trovare i giusti parametri $n$ e $\chi$. Con una procedura di reverse-engineering, gli autori ottengono i valori

$$\chi(T) = F(\phi^{\mathrm{I}}, \phi^{\mathrm{II}}) \quad n(T) = G(\phi^{\mathrm{I}}, \phi^{\mathrm{II}}),$$

dove $F$ e $G$ sono opportune funzioni, con $\phi^{\mathrm{I}}$ e $\phi^{\mathrm{I}}$ che possono essere ottenuti direttamente dagli esperimenti per ogni valore di temperatura $T$. Questa costituisce l’unica soluzione, per i due parametri $\chi(T)$ e $n(T)$, compatibile proprio con gli esperimenti.

 

Figura. L’amido mitiga i grumi di proteine. a) Diagramma di fase dello stato della salsa in funzione della percentuale di amido rispetto all’acqua e della temperatura in gradi Celsius. Ogni riquadro contiene un’istantanea della miscela di salsa scattata durante l’esperimento e il suo contorno riflette l’allungamento medio del campione corrispondente tramite la mappa dei colori mostrata a sinistra. La “fase mozzarella” indica una regione del diagramma di fase in cui il formaggio nel campione forma un grumo di dimensioni comparabili a quelle del sistema. b) Lo stesso diagramma di fase di a) dopo la levigatura gaussiana è rappresentato come una mappa di calore discreta con la mappatura dei colori che rappresenta l’allungamento medio del campione. c) Levigatura della regressione del kernel del diagramma di fase in a) per ottenere una mappa continua. La mappa dei colori a destra si riferisce ai pannelli b) e c). Figura tratta da “Phase behavior of Cacio and Pepe sauce”.

In sinergia, esperimenti ed equazioni rivelano i segreti della perfetta cacio e pepe:

• La presenza di amido, anche in piccole quantità, intorno all’$1\%$, è cruciale per stabilizzare la salsa. L’amido riduce la tendenza delle proteine del formaggio a formare grumi, aumentando la temperatura a cui si osservano le transizioni di fase indesiderate, come quella mozzarella.
• Non lasciarsi ingannare dalle alte temperature Superare una temperatura critica durante la preparazione, tipicamente intorno a $70$-$75°C$, porta alla fase mozzarella. Abbassare la temperatura o attendere che l’acqua si raffreddi prima di aggiungere il formaggio riduce il rischio di grumi.
• L’efficacia della (tanto di moda) risottatura della pasta. In questo modo, si migliora ulteriormente la capacità della salsa di emulsionarsi correttamente, limitando la formazione di aggregati.

Gli autori concludono l’articolo applicando le loro conclusioni al caso di due persone (molto affamate) che vogliono cucinarsi $240$ grammi di tonnarelli cacio e pepe. Forniscono anche delle alternative, come l’uso di amido in polvere, al posto della risottatura. Sebbene non vogliano fare da maestri a chef e professionisti della cucina, pare che, tra matematica e fisica, la vostra cacio e pepe sarà così cremosissima. Non resta che provare!

Marco Menale