Il 13 marzo 2024 è stata inaugurata CUB3S, omaggio\(^3\) aperto e incompleto. La mostra prevede un allestimento fisico nello spazio espositivo PerArtEM presso l’IIS Via Roma 298 di Guidonia e uno virtuale accessibile anche tramite visore VR all’interno del sito web artsteps. Ce ne parla il docente responsabile del progetto Roberto Ianigro.
La mostra è immaginata come un omaggio al cubo necessariamente aperto perché i processi messi in campo sono passibili di approfondimenti e verifiche, incompleto perché sarebbe velleitario pensare di risolvere in tre mosse l’interpretazione del tema. CUB3S delinea un percorso attraverso tre proposte accomunate da una evidente carattere processuale: le scelte progettuali sono state riservate alle strutturazioni logico-matematiche che generano gli esiti rinunciando ad ogni arbitraria formalizzazione.
La narrazione parte dall’essenza del cubo, cioè dalla sua struttura e da alcuni telai da essa sottesi, evolve nella sua forma plastica evidenziata da inter-azioni additive e sottrattive, per concludersi in una esplicitazione fenomenica determinata da azioni proiettive.
incomplete open cube reloaded
Un cubo aperto è formato da un telaio definito dai suoi spigoli ed è incompleto se al telaio mancano una o più aste. L’artista statunitense Sol LeWitt (1928–2007), realizzando Incomplete Open Cubes (1974/82), riduce a 122 i 4094 casi possibili eliminando quelli che non ricostituiscono il volume, che presentano discontinuità o ottenibili da un caso già individuato attraverso una o più rotazioni. Il progetto propone 4 nuovi cubi aperti incompleti (4M, 4V, 6M, 2M2V) e individua una serie formata da 88 casi partendo dal telaio formato dalle mediane delle facce (4M) applicando le stesse tre limitazioni imposte da Sol LeWitt e la stessa procedura logico-grafica. Il risultato è stato poi verificato matematicamente avvalendosi del software Python.

01. Struttura della genesi degli 88 cubi aperti incompleti.
Gli esiti sono esplicitati da una struttura ramificata che mostra come ogni caso con n aste possa essere generato da uno o più casi con n -1 aste e da un modello allestito nello spazio espositivo virtuale.

02. Modello virtuale degli 88 cubi aperti incompleti (allestimento CUB3S su artsteps curato da Roberto Croce – 5E e Roberto Ianigro).
Partendo dal pensiero di Pitagora secondo il quale “la geometria delle forme è musica solidificata” è stata individuata una relazione tra la successione dei cubi aperti incompleti e una composizione musicale: una Partitura per flauti e cubi aperti incompleti basata sul Canone di Johann Pachelbel (1653-1706) esplicitata da una performance in occasione dell’inaugurazione.

03. Partitura per flauti e cubi aperti incompleti, rigo 33 (ideata da Alessandro Fratta e Roberto Ianigro).
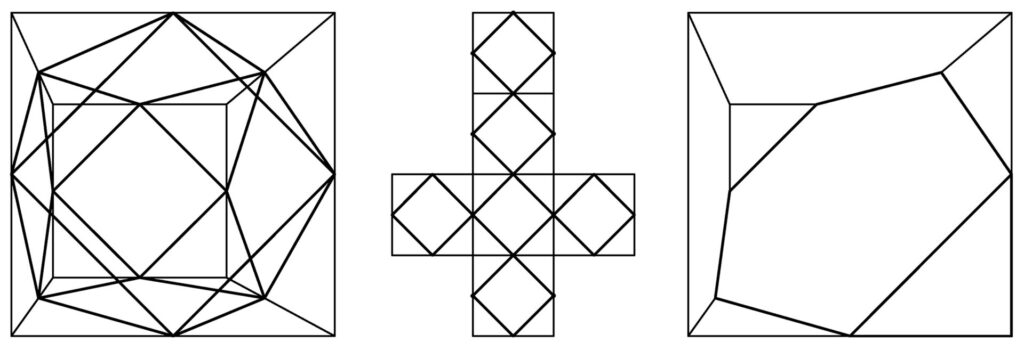
Le coppie di aste contrapposte dei 4 telai individuati possono essere interpretate come intersezioni tra un piano e il cubo stesso. Ogni singolo piano suddivide il cubo in due nuovi solidi: due semicubi.
and or not
Un semicubo si ottiene sezionando un cubo con un piano che lo divide in due solidi di pari volume. Degli infiniti piani che sezionano un cubo in tal modo si considerano solo quelli che intersecano gli spigoli nei vertici o nei punti medi degli spigoli (4M, 4V, 6M, 2M2V). Ognuna delle 25 sezioni genera 2 semicubi per un totale di 50 casi. Le possibili interazioni tra due semicubi all’interno di un cubo vuoto sono quindi 2500.
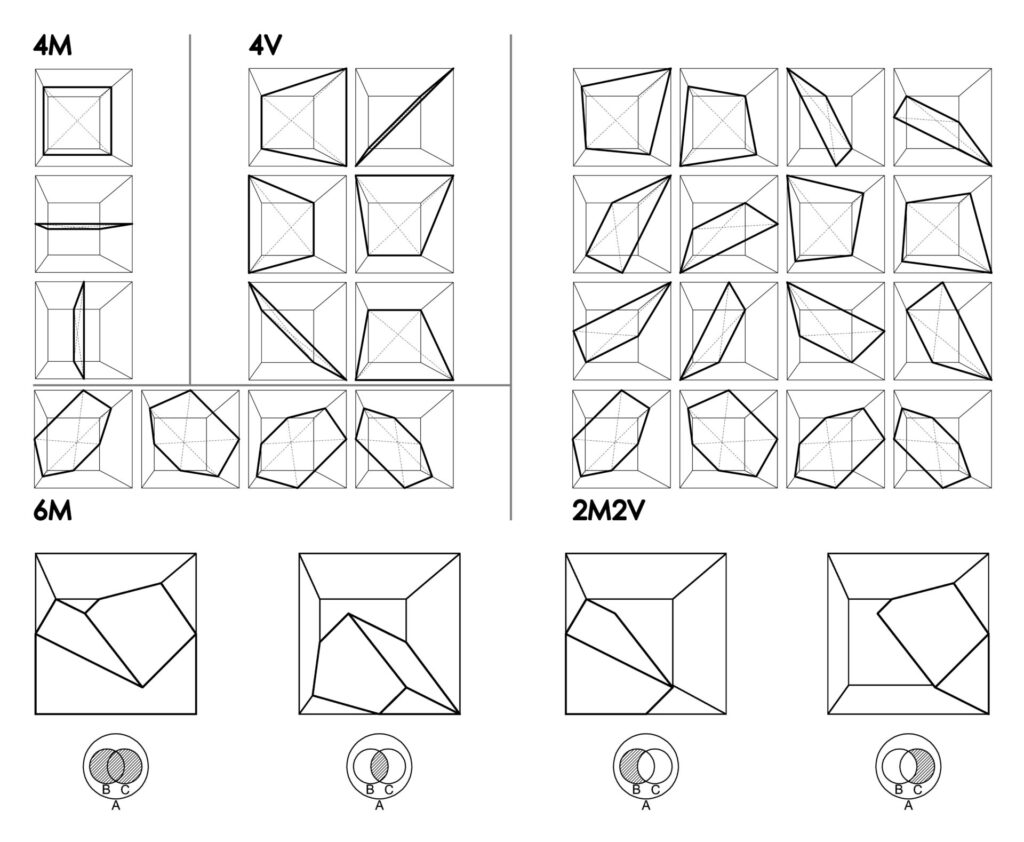
04. Sezioni 4M, 4V, 6M, 2M2V | Operazioni booleane.
È possibile a questo punto definire diverse operazioni facendo riferimento ai diagrammi di Venn e agli operatori booleani. Tre regole escludono alcuni casi: la sovrapposizione dello stesso semicubo, quelli che richiudono il cubo di partenza, quelli ottenibili da un caso già individuato attraverso rotazioni. Applicando una procedura logico-grafica è stato possibile evidenziare 58 casi validi.
La tassonomia delle 58 intersezioni (AND) esplicita il concetto platonico dell’idea già racchiusa nel blocco di partenza, il cubo, che va liberata dal “soverchio” – come sostiene Michelangelo – “per forza di levare”, in questo caso non secondo le intenzioni dell’artista, ma applicando un processo.

05. 9/58 AND, installazione galleggiante (in fondo), 58 OR individuati (in primo piano), 2×4 NOT (sospesi in alto), (allestimento CUB3S su artsteps curato da Roberto Croce – 5E e Roberto Ianigro).
Nove dei 58 AND sono stati impiegati per un’installazione galleggiante realizzata nell’allestimento virtuale mentre i 58 OR, considerati, per ogni caso, come giustapposizione di un AND e due NOT, costituiscono la base per la realizzazione di un board game combinatorio in corso di elaborazione.

06. Prototipo di uno dei pezzi del board game AND OR NOT.
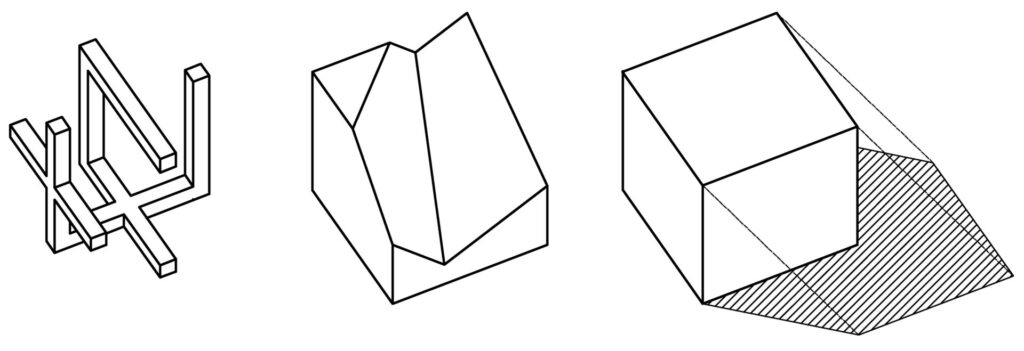
Anche la rappresentazione assonometrica del cubo è il risultato di un’operazione di sezione: la sezione piana delle proiezioni dei suoi spigoli. Individuare il perimetro di tale immagine corrisponde a sua volta alla definizione dell’ombra del cubo nel caso in cui la luce abbia la stessa direzione della proiezione e il piano di proiezione sia lo stesso sul quale viene riportata l’ombra.

shaping sunlight and shadow
Lo scopo del progetto è dare forma plastica all’ineffabile consistenza di luce e ombra. Secondo la teoria delle ombre, definito il fascio di luce che investe un solido, si individuano le ombre proiettate. Il processo prevede di considerare le linee di costruzione come spigoli appartenenti a figure solide. Sezionato il fascio di luce, si formano 2 nuovi volumi: la cristallizzazione della luce e la pietrificazione dell’ombra. La specifica forma ottenuta – la meridiana rotta – è determinata dalla inclinazione dei raggi solari (azimut e elevazione) che varia al variare dalle coordinate geografiche, della data e dell’ora. Se per Hermann Hesse “anche un orologio fermo segna due volte al giorno l’ora esatta” una meridiana rotta solidifica l’ombra prodotta dall’interazione della luce solare con un cubo e, una volta all’anno, non getta ombra e indica correttamente giorno ed ora in un certo punto della Terra, segnando nella memoria la traccia di un evento.

07. Genesi della meridiana rotta: cristallizzazione della luce e solidificazione dell’ombra.
Cinque meridiane rotte in calcestruzzo sono state realizzate in collaborazione con la Buzzi Unicem, l’ultima delle quali è stata progettata nell’ambito delle attività laboratoriali propedeutiche alla mostra, attività che hanno previsto anche la progettazione di un quadrante polare da realizzare presso gli stabilimenti Buzzi Unicem e una installazione che visualizza il significato del Teorema di Pohlke (Archimede, Pohlke e gli esalateri). Il processo è stato approfondito partecipando a due concorsi (Ombre rosse ha ricevuto la menzione speciale alla IX edizione del concorso Tracce di memoria e Matteotti il ponte ha vinto l’VIII Concorso Matteotti per le scuole) e al PCTO Startupper tra i banchi di scuola presso Lazio Innova.

08. Meridiana rotta 1 (Guidonia, 11:30, 06.10.1941, inizio delle attività produttive delle cementerie Buzzi di Guidonia), installazione (calcestruzzo, tondini di acciaio inox, lastra in metacrilato arancione da 1 cm incisa al laser), fotografia di Ivan Giangaspero | Meridiana rotta 5 (Guidonia, 11.46, 7.3.2023, incidente aereo nel quale hanno perso la vita il colonnello Giuseppe Cipriano e il tenente colonnello Marco Meneghello dell’Aeronautica Militare), installazione (calcestruzzo, profili in acciaio inox, semicubo in travertino), fotografia di Roberto Ianigro.
Le scelte allestitive e organizzative sono state effettuate sulla scorta del percorso PCTO Come nasce una mostra MAXXI A[R]T WORK, svolto presso il museo MAXXI di Roma.

09. Archimede, Pohlke e gli esalateri, installazione (murale, 2 cubi in polistirolo di 40 cm di lato, filo di nylon), schema | allestimento, fotografie di Roberto Ianigro.
Roberto Ianigro
Link esterni
Partitura per flauti e cubi aperti incompleti
Video messaggio di Roberto Natalini in occasione dell’inaugurazione
Nota: tutti i progetti sono stati realizzati dagli studenti dell’IIS via Roma 298 di Guidonia (RM) nell’ambito del progetto St.Art |_over e portati a nuovi esiti nei laboratori CUB3S propedeutici alla mostra e alla candidatura al Premio Archimede 2023. Ai laboratori hanno preso parte docenti di matematica, arte, discipline pittoriche e musica. Le attività sono state svolte in collaborazione con BUZZI UNICEM (meridiana 1, 2, 3, 4, 5, riqualificazione urbana piazza di Colle Fiorito, predisposizione per i murales e l’allestimento, strutture in legno e cubi in cls, quadrante polare), 60° STORMO dell’AERONAUTICA MILITARE (meridiana 3, 4 e 5), COMUNE di GUIDONIA MONTECELIO (meridiana 5, riqualificazione urbana piazza di Colle Fiorito), MAXXI ART WORK (PCTO Come nasce una mostra), LAZIO INNOVA (PCTO Startupper tra i banchi di scuola), ROMA STONE (opera plastica Omaggio3), ESTRABA (semicubo per la meridiana 5).















