Formula di Eulero, Teorema di Eulero, Funzione di Eulero, Caratteristica di Eulero, Costante di Eulero, Numeri di Eulero, Metodo di Eulero, … L’elenco potrebbe continuare a lungo; basta scorrere le voci di wikipedia per farsi un’idea. In effetti, Eulero è stato uno dei matematici più prolifici della storia: ha scritto 886 pubblicazioni, tra libri e articoli. È una scommessa pressoché sicura che ogni matematico ha il suo “Teorema di Eulero'” o la sua “Formula di Eulero” preferita. La Matematica è piena di Eulero! è una serie che raccoglie le scelte di alcuni membri del comitato di redazione di MaddMaths!, ai quali abbiamo chiesto di presentare uno di questi argomenti ai nostri lettori e lettrici. Il quinto episodio, “Il metodo di Eulero” è a cura di Francesca Carfora.
Cosa hanno in comune la traiettoria di un corpo in moto, la dinamica di una o più popolazioni, le reazioni chimiche in atmosfera? Come molti fenomeni fisici, molti problemi ingegneristici e molti sistemi biologici, questi esempi possono essere descritti da modelli matematici che utilizzano equazioni differenziali. Se il termine “equazione” risale almeno al Medioevo, al Liber Abaci di Fibonacci, il calcolo differenziale nasce molto dopo, con Newton e Leibniz nel XVII secolo; in un’equazione differenziale, l’incognita è una funzione che deve essere determinata attraverso informazioni sulle sue derivate. In particolare, se si tratta di una funzione di una sola variabile, parliamo di equazioni differenziali ordinarie. Ora, è in genere possibile studiare l’esistenza e l’unicità delle soluzioni, come pure il loro comportamento qualitativo in situazioni di particolare interesse ma, come Eulero sapeva bene, solo in pochi casi è possibile avere una forma analitica della soluzione, o una sua espressione in termini di funzioni elementari.

Frontespizio della prima edizione delle Istituzioni di Calcolo Integrale di Eulero (1768)
Il capitolo 7 della sezione 2 del primo libro delle Institutionum Calculi Integralis di Eulero (pubblicato nel 1768) è dedicato all’integrazione approssimata delle equazioni differenziali. Si apre con la descrizione di quello che oggi chiamiamo “metodo di Eulero”: assegnato il problema ai valori iniziali
\[
\begin{aligned}
y’(x)&=f(x,y)\\\\
y(x_0)&=y_0.
\end{aligned} \qquad (1)
\]
vogliamo approssimare la sua soluzione, cioè la curva \(y=y(x)\) che passa per il punto iniziale \((x_0, y_0)\) e la cui derivata è \(f(x,y)\) . Fissiamo allora un passo \(h\) (per semplificare lo supponiamo costante, ma in realtà è possibile (e consigliabile) scegliere passi diversi \(h_i\) ) e discretizziamo l’intervallo di integrazione ponendo \(x_{i+1} = x_i + h\) per \(i = 0,1,2,…\). A questo punto il valore della soluzione nel nodo \(x_{i+1}\), che indichiamo con \(y(x_{i+1})\), viene approssimato supponendo che la derivata \(f(x,y)\) resti costante nell’intervallo tra \(x_{i}\) e \(x_{i+1}\):
\[y_{i+1} = y_i + h f(x_i,y_i).\]
Questo significa che tra \(x_{i}\) e \(x_{i+1}\) approssimiamo la curva \(f(x,y)\) con la sua retta tangente in \((x_i, y_i)\).
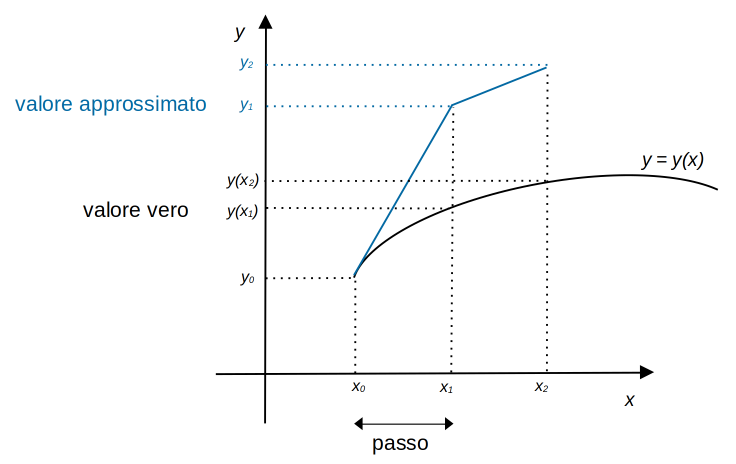
Rappresentazione grafica dei primi due passi del Metodo di Eulero
La figura ci mostra i primi passi del metodo: l’approssimazione \(y_1\) non si trova sulla curva, ma sulla tangente tracciata dal punto \((x_0, y_0)\). Così l’approssimazione \(y_2\) viene costruita tracciando la retta per \((x_1, y_1)\) parallela alla tangente alla curva in \(x_1\).
Cosa può andare storto? Ad ogni passo, \(y(x_i)\) viene approssimato come \(y_i\) e per \(i > 0\) questa approssimazione si basa sulle approssimazioni precedenti. Quindi l’errore si accumula passo dopo passo, anche con conseguenze catastrofiche. Una soluzione ovvia è ridurre il passo, in modo da migliorare l’approssimazione della curva \(y(x)\) con la sua retta tangente, come nella figura seguente.
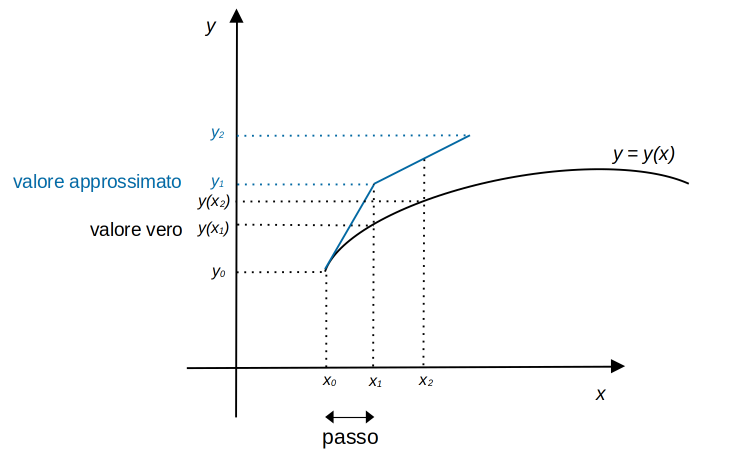
Rappresentazione grafica del Metodo di Eulero con passo dimezzato
Con il linguaggio dell’analisi numerica, il metodo di Eulero è consistente : significa che l’errore locale della nostra approssimazione, quello che commettiamo in un singolo passo partendo da un valore esatto, tende a zero con l’ampiezza del passo. Inoltre ha ordine di convergenza 1: un metodo è convergente se la differenza \( |y_i – y(x_i)|\) , ovvero l’errore globale del metodo al passo \(i\), è infinitesima con il passo \(h\) per ogni \(i\) e l’ordine di questo infinitesimo è detto ordine di convergenza.
L’accuratezza del metodo di Eulero è legata all’approssimazione locale della curva \(y\) con la sua retta tangente, quindi con il polinomio di Taylor di primo grado. Potremmo pensare, per migliorare l’approssimazione, di utilizzare un polinomio di Taylor di ordine maggiore, ma questo richiede la valutazione delle derivate della funzione \(f \). Un’alternativa meno dispendiosa è utilizzare come approssimante in \(x_{i+1}\) una combinazione lineare delle tangenti in \(x_i\) e in un punto dell’intervallo \([x_{i}, x_{i+1}]\):
\[y_{i+1} = y_i + (1-a) h f(x_i,y_i) + a h f\left(x_i + \frac{h}{2a},y_i + \frac{h}{2a} f(x_i,y_i)\right)\]
in modo che l’approssimazione risultante sia di ordine 2. Si ottiene così, ad esempio, il metodo di Eulero modificato, per \(a = 1\):
\[y_{i+1} = y_i + h f\left(x_i + \frac{h}{2},y_i + \frac{h}{2} f(x_i,y_i)\right)\].
L’idea di approssimare la curva \(y(x)\) utilizzando più valutazioni della funzione \(f\) nell’intervallo \([x_{i}, x_{i+1}]\) viene poi generalizzata dai metodi di Runge-Kutta, dal nome dei due matematici tedeschi, Carl Runge (1856-1927) e Martin Kutta (1867-1944), che intorno al 1900 li idearono e perfezionarono. La loro interpretazione può essere più semplice a partire dalla formulazione integrale del problema:
il sistema (1) equivale all’equazione
\[ y(x) = y_0 + \int_{x_0}^x y’(s) ds = y_0 + \int_{x_0}^x f(s,y(s)) ds \]
o in particolare, per il primo intervallo
\[ y(x_1) = y_0 + \int_{x_0}^{x_0+h} f(s,y(s)) ds \]
e questo integrale può essere approssimato non con un rettangolo, come fa il metodo di Eulero che considera un solo valore della funzione \(f\), ma con una combinazione lineare di valori della funzione in più punti dell’intervallo \([x_0,x_0+h]\). Questi punti, come pure i pesi della combinazione lineare, vengono determinati in modo da avere la massima accuratezza possibile della formula.
Tutti i metodi visti finora sono one-step perché costruiscono l’approssimazione di \(y(x)\) in un punto \(x_{i+1}\) guardando solo all’intervallo immediatamente precedente. Esistono metodi multistep che costruiscono questa approssimazione utilizzando informazioni relative a un certo numero \(k\) di intervalli precedenti. Ovviamente, questi metodi richiedono una inizializzazione: i primi valori approssimati \(y_1, y_2, …, y_{k-1} \) devono essere calcolati in altro modo, ad esempio con il metodo di Eulero.
Ancora, abbiamo dato per scontato che i metodi di approssimazione descritti fossero espliciti, cioè che l’approssimazione \(y_{i+1}\) potesse essere costruita operando sui valori precedentemente calcolati \(y_1, y_2, …, y_i \). Esistono poi metodi impliciti, in cui si utilizza la valutazione della funzione \(f\) anche nell’estremo \(x_{i+1}\): poiché allora la nuova approssimazione compare in entrambi i lati della formula, è necessario risolvere un’equazione per calcolarla. L’esempio più semplice è il metodo di Eulero implicito:
\[ y_{i+1} = y_i + h f(x_{i+1},y_{i+1});\]
combinando infine i due metodi, l’esplicito e l’implicito, si ottiene l’ottimo metodo dei trapezi, o di Crank-Nicolson:
\[ y_{i+1} = y_i + \frac{h}{2} \left[ f(x_i,y_i) + f(x_{i+1},y_{i+1})\right].\]
I metodi impliciti sono più costosi, poiché ad ogni passo va risolta un’equazione; hanno però il vantaggio di essere più stabili. Il concetto di stabilità riguarda il comportamento dell’approssimazione al crescere del numero di passi quando il passo resta costante. Se la curva che stiamo approssimando è limitata, è naturale richiedere che anche la sua approssimazione si mantenga tale. Intuitivamente, il metodo di Eulero implicito è più stabile perché impone il controllo sulla pendenza della curva \(y\) anche sul secondo estremo \(x_{i+1}\) dell’intervallo di approssimazione.
Per concludere, se volete scoprire come un matematico applicato utilizza i modelli differenziali, vi suggerisco una piacevole lettura. Se invece avete voglia di sperimentare l’applicazione di questi metodi numerici, variando le condizioni, l’ampiezza del passo, la forma dell’equazione, o anche confrontando le prestazioni dei diversi metodi, Wolfram Alpha mette a disposizione un risolutore numerico online che vi consente di esplorare tutti questi aspetti con grande semplicità. Buon divertimento!




















Trackback/Pingback