Le dimostrazioni sono il cuore della matematica, ma insegnarle a scuola è una sfida complessa. OILER, una piattaforma online dedicata alla didattica della logica, propone un percorso che parte dai giochi e dalle strategie vincenti per guidare studenti e studentesse, anche di primaria, verso la dimostrazione. Questo articolo è stato scritto da Luigi Bernardi.

Lavorare sulla dimostrazione in matematica è croce e delizia degli insegnanti. Sul linguaggio e sul ragionamento si cerca di lavorare fin dai primi anni dell’educazione, ma per gli aspetti formali della dimostrazione si aspetta l’ultimo anno di secondaria di primo grado o, più frequentemente, l’inizio della secondaria di secondo grado, con la geometria. Sempre che lo si faccia.

Tuttavia… per lavorare sulla dimostrazione non è necessario parlare di dimostrazione. Nelle seguenti righe proviamo a sciogliere l’apparente contraddizione.

LOVLEIS (che prende il nome da Ada Lovelace) è un percorso didattico che tratta di giochi a due giocatori. L’idea del percorso è che gli studenti seguano un itinerario fiabesco di cui sono i protagonisti, visitando varie località fantastiche, ognuna legata a giochi con caratteristiche specifiche. Uno degli obiettivi del percorso è chiarire il concetto di strategia in un gioco, cioè un insieme di comportamenti stabiliti a priori che permette di raggiungere un certo esito. Il percorso è stato sperimentato con classi di vari livelli scolastici, dalla quarta primaria alla quinta liceo. Nel seguito, analizzeremo alcune produzioni relative alla scuola primaria.

 

L’INIZIO DEL PERCORSO EDUCATIVO

Si comincia leggendo in classe il racconto, accompagnato da immagini proiettate alla L.I.M. per rendere la storia più immersiva.

In una domenica di un pomeriggio di primavera, la classe sta giocando a palla in piazza. Tutti ridono e si divertono, mentre la palla vola di qua e di là. A un certo punto, la palla viene tirata troppo forte e finisce dentro uno strano portone socchiuso.

La classe entra così in un mondo fantastico, e finisce nella città di Tictactò (Tic-Tac-Toe è il nome inglese del Tris). Come si può immaginare, nella città ogni abitante è appassionato del gioco del Tris.

Dopo aver lasciato la classe libera di fare qualche partita, si organizza un torneo di Tris, in modo che gli studenti sviluppino strategie intuitive.

Un incontro inaspettato porta a un punto centrale dell’attività.

Durante i festeggiamenti, un uomo dall’aspetto timido e gentile si avvicina alla classe. Si presenta come Timoteo e, con gli occhi pieni di speranza, racconta il suo dilemma. Gioca spesso a Tris con sua sorella Celeste, ma non riesce mai a vincere. Celeste comincia sempre per prima, posizionando audacemente la sua “X” al centro della griglia. Timoteo, visto il talento della classe nel gioco, chiede disperatamente di aiutarlo a trovare un modo per non perdere più contro sua sorella.

Si comincia quindi il lavoro di produzione delle lettere a Timoteo; cioè – in termini tecnici – viene chiesto alla classe di trovare una strategia non perdente per il secondo giocatore a patto che il primo cominci dal centro. La consegna di scrivere una lettera a Timoteo è ben più coinvolgente rispetto a una richiesta diretta di una strategia, probabilmente nemmeno comprensibile a una classe di primaria.

Prima di proseguire con l’analisi delle produzioni degli studenti, facciamo una breve pausa teorica.

 

MA COSA C’ENTRANO LE STRATEGIE CON LE DIMOSTRAZIONI?

Nella teoria della dimostrazione matematica, l’isomorfismo di Curry-Howard equipara le dimostrazioni ai programmi informatici. Accanto a dimostrazioni e programmi, si inserisce presto un terzo attore, con il lavoro pionieristico “Logica Dialogica” (Dialogische Logik, 1978) di Paul Lorenzen e Kuno Lorenz. Il filone di ricerca è noto come Game Semantics (ossia dove l’interpretazione delle prove, i.e., la semantica, viene data in termini di gioco). La verità matematica di un enunciato è definita mediante un gioco fra un proponent P e un opponent O: P afferma che l’enunciato è vero, mentre O sostiene che sia falso, e i due ingaggiano una discussione al riguardo. L’idea centrale è che P cerca di far arrivare O a una contraddizione. L’enunciato è considerato vero se P ha una strategia vincente, e falso se ce l’ha O.

Esistono vari giochi formali per attribuire un valore di verità a una formula, ma in generale il “gioco della dimostrazione” si svolge fra due giocatori con informazione perfetta e completa, non ammette patta, è asimmetrico (ossia i due giocatori seguono regole radicalmente differenti). Inoltre svolge un ruolo fondamentale il concetto di partita infinita (se una partita dura all’infinito, vince O).

 

DIFFICOLTÀ NELL’ESPORRE UNA STRATEGIA

L’equivalenza teorica fra strategie e dimostrazioni si riflette sul piano didattico: le difficoltà che gli studenti più grandi hanno nel trovare ed esporre una dimostrazione sono molto simili a quelle che gli studenti di primaria hanno nel trovare ed esporre una strategia.

Durante la prima attività, come abbiamo visto, viene chiesto alla classe – lavorando a coppie – di scrivere una lettera destinata a un personaggio chiamato Timoteo, per aiutarlo a non perdere più contro sua sorella Celeste nel gioco del Tris. La prima difficoltà, emersa in quasi tutte le coppie di studenti, è stata comunicare efficacemente la sequenzialità della strategia (Figura 1).

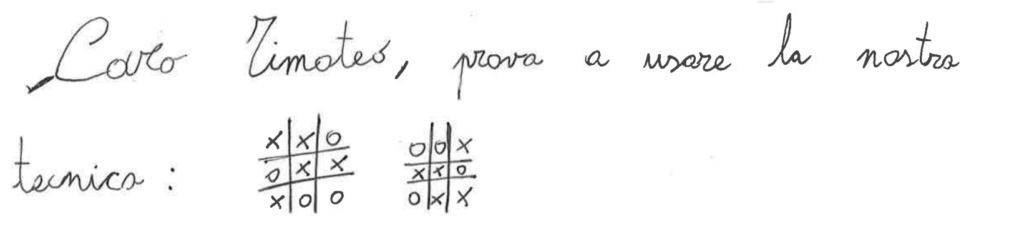
Figura 1

Infatti, osservando solo la posizione finale di una partita, Timoteo non può sapere quale mossa fare in quale momento. Dopo aver discusso il problema con gli studenti, molti hanno pensato di risolverlo aggiungendo numeri come indici delle mosse fatte (Figura 2).

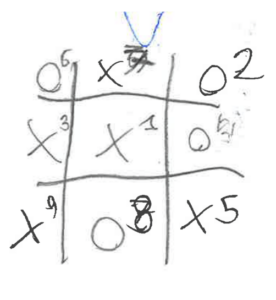
Figura 2

Diviene ora esplicito un problema cruciale: come si può essere sicuri della mossa che farà Celeste? La quasi totalità degli studenti ha trascurato la generalità della strategia, esaminando solamente uno scenario particolare in cui Timoteo riesce a vincere o pareggiare (Figura 3). In sintesi, sono state identificate due profonde sfide concettuali che si incontrano nel descrivere una strategia: è essenziale anzitutto esprimere con chiarezza l’ordine delle mosse che portano a una certa situazione e, in secondo luogo, realizzare che una strategia deve avere carattere generale e considerare tutte le possibilità, poiché non si possono prevedere in anticipo le mosse dell’avversario.

Figura 3

Le dinamiche qui descritte sono perfettamente comparabili con le difficoltà che gli studenti più grandi incontrano nelle dimostrazioni (Selden & Selden, 2007; Stylianides et al., 2016).

Annie Selden e John Selden riportano come alcuni studenti, anche dopo un lavoro specifico, confondano le evidenze empiriche con la dimostrazione deduttiva. Questa difficoltà è presente quando si parla di strategie vincenti nella scuola primaria: gli esempi tentano di supplire alla mancanza di generalità.

Il report dei Selden prosegue evidenziando un’altra difficoltà: la mancata comprensione del significato dei quantificatori e del fatto che il loro ordine sia rilevante. Perfino alcuni studenti universitari spesso non colgono l’importanza dell’ordine dei quantificatori, ritenendo erroneamente che scambiare fra loro un quantificatore esistenziale e un universale non abbia conseguenze. Nel nostro contesto l’alternarsi dei quantificatori è un concetto chiave: l’esistenziale corrisponde all’istruzione data alla persona per cui stiamo costruendo la strategia, l’universale alla generalità della mossa dell’avversario.

 

IL RESTO DEL PERCORSO EDUCATIVO

Il percorso educativo continua affrontando altri giochi a due tenendo saldo il riferimento teorico della Game Semantics: si introducono giochi senza patta, asimmetrici e potenzialmente infiniti, con condizioni di vittoria per uno dei due giocatori in caso di partita infinita. L’ipotesi di lavoro è che, tuttavia, prima di introdurre un gioco dove non esiste la patta è meglio introdurre un gioco dove esiste la patta, prima di parlare di giochi asimmetrici conviene parlare di giochi simmetrici, prima di discutere giochi potenzialmente infiniti è meglio limitarsi a giochi finiti.

Su questa idea si sviluppa tutto il percorso di LOVLEIS. Dopo il gioco del Tris, viene presentato il gioco Tris a perdere, dove chi fa tris perde e dunque il proprio obiettivo è costringere l’avversario a fare tris. Il gioco del Tris a perdere appare estremamente intrigante: negare le condizioni di vittoria stravolge le dinamiche di gioco (sfidiamo il lettore a non perdere contro i furfanti in questa implementazione online del gioco). Viene poi presentato il Pick 15, un gioco numerico che è sorprendentemente isomorfo al Tris. Nel gioco bisogna usare i numeri dall’1 al 9 per ottenere somma 15 con tre di essi: il punto centrale dell’isomorfismo è il quadrato magico. Nel percorso si discutono poi altri giochi, fra cui citiamo la corsa al 20 (chiamata nel percorso Leva Leva), di cui fa un celebre uso Guy Brousseau nell’introduzione al suo Teoria delle Situazioni Didattiche. Il percorso finisce con il Gioco delle Oche (un gioco da noi inventato, fedele trasposizione del “gioco della dimostrazione”).

Il lavorare sulle strategie sembra presupporre un lavoro su quantificatori e relative regole di argomentazione, ed è su questa idea che continueremo la nostra discussione…

Alla prossima!

Guarda la pagina  AILA x MaddMaths!