Una mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. In questa prima puntata scopriremo cosa studia la topologia partendo da due semplici triangoli. Trovate tutte le puntate su questa pagina.

Molto probabilmente la prima volta che avete sentito parlare di topologia vi è stato detto che essa è quella parte della matematica che si occupa dello studio delle “deformazioni senza strappi o cuciture”, portando il classico esempio che, in topologia, una tazza ed una ciambella sono viste come lo stesso oggetto in quanto possiamo passare da una all’altra mediante appunto una deformazione che non strappa o incolla insieme dei pezzi. Ma qual è il significato di tutto ciò? Perché a un certo punto i matematici hanno deciso che c’era bisogno di trattare queste trasformazioni? E a che cosa può servire studiarle?

Immaginate di voler studiare i due triangoli rossi in figura, magari di dover calcolare la loro area e perimetro. Se voleste procedere rigorosamente dovreste determinare separatamente i lati e le altezze di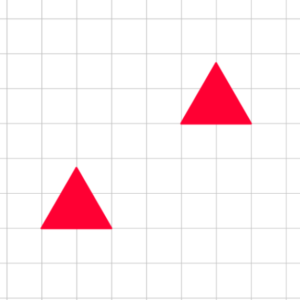 ciascuno dei due e poi calcolare le rispettive aree… ma chi ne ha voglia?! È molto più veloce accorgersi che i due triangoli sono “uguali”, nel senso che hanno lati, altezza e angoli uguali e che quindi, per quel che ci interessa, possono essere trattati esattamente allo stesso modo, come fossero uno stesso triangolo; insomma basta calcolare area e perimetro di uno dei due, l’altro dovrà per forza averli uguali! In effetti basta spostare, o per essere più precisi traslare, uno sull’altro ed accorgersi che essi andrebbero a coincidere perfettamente.

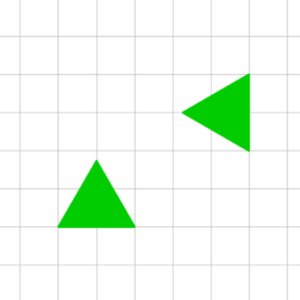Che possiamo dire invece dei triangoli verdi? Di nuovo, finché siamo interessati solamente ad area e perimetro, non c’è alcuna differenza tra i due, basta ruotarne uno e traslarlo e coinciderebbe esattamente con l’altro, risultando quindi equivalenti per i nostri scopi! Anche per i triangoli gialli possiamo sbrigarcela velocemente:  sono evidentemente la stessa figura ma riflessa, capovolta sottosopra, ma intuiamo che questo movimento non va ad intaccare area e perimetro e quindi questi parametri saranno uguali per i due triangoli. Quindi, finché siamo interessati solo ad area e perimetro, non ci interessa come “sono messe” le figure: quelle che, usando traslazioni, rotazioni e riflessioni, possono essere fatte coincidere dovranno avere stessa area e perimetro, e saranno per noi equivalenti. Fin qui sembra tutto abbastanza semplice, no? Lo è, ma al tempo stesso stiamo facendo qualcosa di molto profondo: stiamo dichiarando equivalenti tutte le figure che possono essere fatte coincidere usando specifiche trasformazioni, e questa osservazione permette di semplificare enormemente il nostro ambiente di lavoro. Ma possiamo andare oltre.

Guardate i due triangoli blu. Se foste ancora interessati alla loro area e perimetro direste immediatamente che sono diversi, non equivalenti, ma che direste in merito ad altre loro caratteristiche come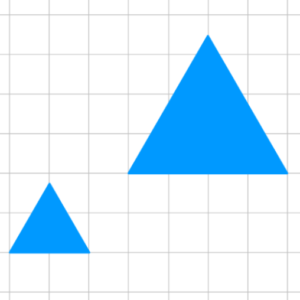 ad esempio la misura degli angoli? Sono uguali, non è così? In effetti “gonfiando”, dilatando uniformemente una figura, i suoi angoli rimangono gli stessi, e neanche ruotarla, traslarla o rifletterla ha effetto sugli angoli. Quindi se siamo interessati a questa caratteristica possiamo allargarci un po’ di più rispetto a prima, possiamo ammettere più trasformazioni: figure che possono essere fatte coincidere usando dilatazioni, traslazioni, riflessioni o rotazioni sono per noi equivalenti finché ci interessiamo alla misura degli angoli.

In sintesi, a seconda delle caratteristiche di un oggetto che ci interessano possiamo introdurre varie trasformazioni e dichiarare equivalenti tutti gli oggetti che possono essere fatti coincidere usando proprio queste trasformazioni: questo è il cuore del fare geometria. Possiamo allora ammettere trasformazioni via via più numerose e generali, fino ad arrivare a poter trattare gli oggetti come fossero fatti del pongo con cui giocavamo da bambini, cioè potendoli deformare e contrarre a nostro piacimento: l’unica cosa che vietiamo è di strapparli, bucarli o incollarli tra loro. Se ammettiamo queste deformazioni, che in gergo vengono dette omeomorfismi (dal greco “forma simile”), stiamo facendo topologia. Ecco che in topologia un cubo ed una sfera diventano equivalenti, così come saranno equivalenti un triangolo ed un qualunque poligono o, come nel celebre esempio citato inizialmente, una tazza ed una ciambellina.

In topologia non siamo più interessati a perimetro, area o angoli, ma a caratteristiche geometriche più generali, cioè a come gli oggetti “si collocano” nello spazio, in che modo essi “raggruppano punti”. Il motivo è che molti problemi geometrici non dipendono tanto dalla forma degli oggetti in considerazione quanto piuttosto da come essi, appunto, si collocano nello spazio: il classico esempio è quello dei 7 ponti di Konigsberg, dove si deve cercare un modo per attraversare la città passando esattamente una volta su ciascuno dei 7 ponti. Il problema chiede solo di individuare un percorso senza curarsi della sua lunghezza, di conseguenza non ci interessano né la lunghezza dei vari ponti né la distanza tra di essi, ma solamente come questi collegano i vari quartieri, quindi possiamo deformare questi ponti a nostro piacimento (ma senza spezzarli o unirli, altrimenti cambierebbe il loro numero!) e la natura del problema non cambierebbe.

La potenza della topologia sta nel fatto che essa non dipende dalla nozione di misura, possiamo cioè trattare oggetti senza preoccuparci di dover misurare qualcosa (che siano lunghezze, aree, angoli,…) e questo ci permette di lavorare con strutture estremamente generali, non per forza “misurabili” (delle quali si occupa la teoria della misura, ma non noi, per ora).
I problemi che possono essere affrontati con un approccio di questo tipo sono innumerevoli, motivo per cui ad oggi la topologia è considerata una delle branche fondamentali della matematica trovando applicazioni nei contesti più disparati, dalla fisica (si veda il premio Nobel per la fisica del 2016) alla biologia, passando per l’analisi dei dati, la robotica e lo studio delle reti neurali (le intelligenze artificiali più sofisticate)… dire che in ogni disciplina scientifica si incontra almeno un risultato che viene dalla topologia non sembra essere una frase troppo azzardata.
Come scopriremo nelle prossime puntate, la topologia è veramente in grado di trattare tutto il mondo che ci circonda.

1 – continua

Gabriele Belegni

Gabriele Belegni, laureato in Matematica teorica e studente magistrale in Matematica applicata presso l’Università di Camerino. Mi occupo anche della divulgazione matematica nelle sue varie forme: articoli, conferenze e laboratori.