Dopo una lunga pausa, la quinta puntata della rubrica “Uno sguardo oltre la superficie“, a cura di Giuseppe Tinaglia. Uno spazio dove si osserva la geometria che ci circonda, ma anche oltre.
Il problema isoperimetrico consiste nella seguente domanda: Dato un numero L, qual è la curva chiusa nel piano di lunghezza L che racchiude la massima area? Nella tabella seguente ci sono tre esempi.
\[
\begin{array}{|c|c|c||c|}
\hline
&Quadrato& Triangolo Equilatero& Cerchio\\
\hline
Perimetro&1&1&1\\
\hline
Area&\frac{1}{16}=0,0625&\frac{\sqrt{3}}{36}\sim 0,0481&\frac{1}{4\pi}\sim 0,0796\\ \hline
\end{array}
\]
Quindi, tra gli esempi sopra, il cerchio è la figura geometrica che a parità di perimetro, racchiude la maggiore area. Non è certo un caso visto che è proprio il cerchio ad essere la soluzione del problema isoperimetrico. E come spesso accade in matematica, non solo siamo in grado di dare una risposta qualitativa a tale domanda, il cerchio, ma bensì anche una più soddisfacente risposta quantitativa. Più precisamente, tra area A e perimetro L di una figura vale sempre la seguente disuguaglianza:
\[\frac{A}{L^2}\leq \frac{1}{4\pi}\]
Inoltre, l’uguaglianza, ovvero il valore massimo possibile del rapporto \(\frac{A}{L^2}\) è ottenuta soltanto dal cerchio. Ottenendo il valore massimo nel rapporto \(\frac{A}{L^2}\) il cerchio, a parità di perimetro (il denominatore), racchiude l’area maggiore (il numeratore).
Prima di raccontare la storia di come si sia arrivati a questa formula, vorrei fare notare che se si vuole stabilire una relazione valida tra area e perimetro, il perimetro al denominatore deve essere necessariamente considerato al quadrato. Questo perché se si prende una figura e si moltiplicano le sue lunghezze per un fattore \(R\), il nuovo perimetro viene moltiplicato per \(R\) mentre l’area per \(R^2\). Si pensi al cerchio di raggio \(R\) la cui lunghezza è \(2\pi R\) mentre l’area racchiusa è \(\pi R^2\). Oppure al quadrato di lato \(R\) il cui perimetro è \(4R\) mentre l’area è \(R^2\). Oppure… ci siamo capiti.[1 ]Questa discussione è analoga a quella contenuta nel mio articolo precedente sul rapporto tra l’area e il volume https://maddmaths.simai.eu/rubriche/matematica-oltre/uno-sguardo-oltre-la-superficie/ippopotami-non-possono-volare/
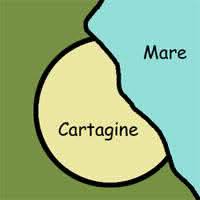
Il problema isoperimetrico è un problema di origini molto antiche. Nell’Eneide, Virgilio racconta di come la principessa Didone, in fuga, approdò sulle coste della odierna Libia e lì chiese al re del luogo un pezzo di terra sul quale fondare una città, la futura Cartagine. Il re si volle prendere gioco di Didone #metoo. Le diede una pelle di bue e le disse che le avrebbe dato tanta terra quanta ne fosse capace di ricoprire con tale pelle. In altre parole, non certo abbastanza per fondare una città! Qui a dire il vero il racconto di Virgilio finisce ma la tradizione racconta che l’astuta Didone abbia tagliato la pelle in una striscia lunga e sottile che sistemò a forma di semicerchio e con gli estremi in mare. Il problema isoperimetrico ci dice che, in questo modo, Didone riuscì a cingere il più vasto terreno possibile.[2 ] Dall’Eneide: Giunsero in questi luoghi, ov’or vedrai/sorger la gran cittade e l’alta ròcca/de la nuova Cartago, che dal fatto/Birsa nomossi, per l’astuta merce/che, per fondarla, fêr di tanto sito/quanto cerchiar di bue potesse un tergo.
Se Didone fosse a conoscenza che il cerchio è la soluzione del problema isoperimetrico non ci è dato sapere. Tuttavia, probabilmente non avrebbe saputo dimostrarlo. Il primo passo verso la scoperta che il cerchio è la soluzione del problema isoperimetrico viene generalmente attribuito a Zenodoro, un matematico greco della seconda metà del II secolo A.C. Egli dimostrò che dato un qualsiasi poligono il rapporto \(\frac{A}{L^2}\) è sempre minore di \(\frac{1}{4\pi}\), il valore che si ottiene per il cerchio. Ottimo. Il caso è chiuso… per quanto riguarda I poligoni. E le altre curve? Per quelle bisogna aspettare più o meno 2000 anni! Precisamente, bisogna aspettare l’arrivo di Jacob Steiner,[3 ]J. Steiner, Einfache Beweise der isoperimetrischen Hauptsatze, J. Reine Angew. Math. 18(1838) 281– 296. un matematico svizzero del XIX secolo. Prima di Steiner, i tentativi di risolvere il problema isoperimetrico erano state futili battaglie a colpi di calcolo algebrico, stile quadratura del cerchio. Con Steiner l’approccio diventa decisamente più geometrico e, anche se il suo metodo era evidentemente efficace, egli fu molto osteggiato dai matematici dei suoi tempi #poteriforti.

J. Steiner
Il problema isoperimetrico si può riformulare in maniera seguente. Qual è la figura che ottiene il massimo del rapporto
\(\frac{A}{L^2}\)? Esattamente quello che Steiner dimostra è questo:
Data una curva chiusa che non è il cerchio, è sempre possibile deformarla in maniera tale da aumentare il rapporto
\(\frac{A}{L^2}\). Quindi, una curva che non è il cerchio non può essere la soluzione del problema isoperimetrico: non può certamente ottenere il massimo nel rapporto \(\frac{A}{L^2}\) se è possibile deformarla e aumentare il rapporto! Missione compiuta. La soluzione non può essere altro che il cerchio!
Missione compiuta? Non proprio. Malgrado la soluzione finale del problema isoperimetrico venga attribuita a Steiner, c’è una falla nel suo modo di ragionare. E’ un problema molto delicato ma il fatto che una curva che non è il cerchio non possa essere la soluzione, non vuole dire necessariamente che la soluzione debba essere il cerchio… la soluzione potrebbe non esistere proprio! E’ il cosiddetto problema di esistenza. Il fatto che esista una figura geometrica tale che il rapporto \(\frac{A}{L^2}\) ottiene il suo valore massimo deve essere dimostrato. Perché se tale figura geometrica non esistesse, allora il ragionamento di Steiner non servirebbe a niente. Più correttamente la domanda da farsi dovrebbe essere: Esiste una figura che ottiene il massimo del rapporto \(\frac{A}{L^2}\)? E se esiste, qual è?
Siccome ho il sospetto di avere perso qualcuno, chiedo aiuto a Oskar Perron,[4 ]O. Perron, Zur Existenzfrage eines Maximums oder Minimums, Jahresber. Deutsch. Math.-Verein. 22 (1913) 140–144. matematico tedesco del XX secolo che con umorismo illustrò il problema nella dimostrazione di Steiner. Usando il ragionamento di Steiner si riesce infatti a dimostrare che 1 è il numero intero più grande di tutti. Come?

O. Perron
Seguendo l’esempio di Steiner, prendiamo un numero intero che non sia uno (una figura che non sia il cerchio), dopo averlo moltiplicato per sé stesso (dopo avere applicato il “metodo Steiner”), si ottiene sempre un numero più grande (si ottiene sempre una figura il cui rapporto\(\frac{A}{L^2}\) è più grande). Quindi nessun numero che non sia uno, può essere il numero intero più grande. ALLORA il numero più grande è 1. Si vede chiaramente in questo esempio di Perron che ALLORA non funziona proprio. E non funziona perché il “più” grande tra i numeri interi non esiste.
Non è un caso che Perron sia un analista e quindi consapevole delle insidie poste dal problema di esistenza. Malgrado l’errore, la soluzione del problema isoperimetrico viene attribuita a Steiner perché con i suoi metodi, cosa che lui non fece o perlomeno non fece nel dettaglio, si riesce anche a costruire la soluzione. Si dimostra che usando il “metodo Steiner” si converge alla soluzione, ovvero al cerchio. Detto questo però, la risoluzione del problema di esistenza deve aspettare i lavori di Karl Weierstrass, un altro matematico tedesco, un analista come Perron, a cui va il merito di avere costruito le fondamenta di un moderno studio del calcolo delle variazioni.[5 ]K. Weierstrass, Mathematische Werke, vol. 7, Mayer & Muller, Berlin, 1927.
Il problema isoperimetrico si può molto semplicemente generalizzare in altre dimensioni. Per esempio: nello spazio Euclideo ci si può porre la domanda seguente: Data un’area A, qual è la superficie di area A che racchiude volume V massimo? Non solo la soluzione di questo problema è la sfera ma, in maniera analoga al caso a due dimensioni, è valida la seguente disuguaglianza
\[\frac{V^2}{A^3}\leq\frac{1}{36\pi}\]
e l’uguaglianza è ottenuta solo dalla sfera. E poi c’è anche la versione n-dimensionale…
La storia di come sia stato risolto il problema isoperimetrico a 3 e dimensioni maggiori è molto più tortuosa e la lasciamo per un altro articolo. La dimostrazione è molto più complessa di quella nel piano. Ad esempio, nel piano si dimostra facilmente che la soluzione del problema isoperimetrico deve essere una figura convessa[6 ]Si guardi la figura all’inizio dell’articolo. mentre questo non è così semplice in altre dimensioni. Un aneddoto interessante è come la soluzione del problema isoperimetrico a 3-dimensioni appaia in un argomento che Poincaré utilizzò per quella che forse è la prima rigorosa dimostrazione che la terra è una sfera o quasi.[7 ]H. Poincaré, Sur un théorème de M. Liapounoff relatif à l’équilibre d’une masse fluide, C. R. Acad. Sci. Paris 104 (1887), 622-625.
- Primo passo: caratterizzare la terra come un corpo fluido omogeneo in equilibrio stabile sul quale agiscono soltanto forze interne di tipo gravitazionale.
- Secondo passo: dimostrare che, fissato il volume, un tale corpo ha necessariamente capacità elettrostatica minima.
- Passo finale: usare la soluzione del problema isoperimetrico nello spazio e un po’ di calcolo delle variazioni, per dimostrare che un corpo con capacità elettrostatica minima deve essere una sfera.
Poincaré è certamente più famoso per la cosiddetta congettura di Poincaré, ora un teorema, dimostrata nel 2002/03 dal matematico Russo Grigori Pereleman.[8 ]Pereleman: The entropy formula for the Ricci flow and its geometric applications.arXiv:DG/0211159, Ricci flow with surgery on three-manifolds.arXiv:DG/0303109., Finite extinction time for the solutions to the Ricci flow on certain three-manifolds.arXiv:DG/0307245.
Ci sono altri modi di generalizzare il problema isoperimetrico. Per esempio, invece che considerare una curva chiusa nel piano, si può studiare la relazione tra l’area e il perimetro per curve chiuse sulla sfera o in altre geometrie non Euclidee. Ma questa è un’altra storia, o un altro atto.
Questo articolo è stato più che ispirato dai seguenti articoli nei quali il lettore interessato può trovare molti più dettagli sul problema isoperimetrico.
- Viktor Blasjo, The isoperimetric problem, Amer. Math. Monthly, 112 (2005), no.6, 526-566.
- Robert Osserman, The isoperimetric inequality, Bull. Amer. Math. Soc., Volume 84, Number 6 (1978), 1182-1238.
Giuseppe Tinaglia
King’s College London
Note e riferimenti
| ⇧1 | Questa discussione è analoga a quella contenuta nel mio articolo precedente sul rapporto tra l’area e il volume https://maddmaths.simai.eu/rubriche/matematica-oltre/uno-sguardo-oltre-la-superficie/ippopotami-non-possono-volare/ |
|---|---|
| ⇧2 | Dall’Eneide: Giunsero in questi luoghi, ov’or vedrai/sorger la gran cittade e l’alta ròcca/de la nuova Cartago, che dal fatto/Birsa nomossi, per l’astuta merce/che, per fondarla, fêr di tanto sito/quanto cerchiar di bue potesse un tergo. |
| ⇧3 | J. Steiner, Einfache Beweise der isoperimetrischen Hauptsatze, J. Reine Angew. Math. 18(1838) 281– 296. |
| ⇧4 | O. Perron, Zur Existenzfrage eines Maximums oder Minimums, Jahresber. Deutsch. Math.-Verein. 22 (1913) 140–144. |
| ⇧5 | K. Weierstrass, Mathematische Werke, vol. 7, Mayer & Muller, Berlin, 1927. |
| ⇧6 | Si guardi la figura all’inizio dell’articolo. |
| ⇧7 | H. Poincaré, Sur un théorème de M. Liapounoff relatif à l’équilibre d’une masse fluide, C. R. Acad. Sci. Paris 104 (1887), 622-625. |
| ⇧8 | Pereleman: The entropy formula for the Ricci flow and its geometric applications.arXiv:DG/0211159, Ricci flow with surgery on three-manifolds.arXiv:DG/0303109., Finite extinction time for the solutions to the Ricci flow on certain three-manifolds.arXiv:DG/0307245. |