Il progetto NEMESIS -NEw generation MEthods for numerical SImulationS– è stato di recente finanziato nell’ambito dell’ERC Sinergy Grant 2023. Paola Antonietti, professoressa di Analisi Numerica presso il Dipartimento di Matematica del Politecnico di Milano, ne è Principal Investigator insieme a Lourenco Beirao da Veiga (Università degli Studi di Milano Bicocca, Italia), Daniele A. Di Pietro (Università di Montpellier, Francia) e Jérôme Droniou (CNRS, Francia).
Ci racconta il progetto NEMESIS proprio Paola Antonietti.
L’ERC e il Synergy Grant
Lo European Research Council (ERC) è l’organismo dell’Unione Europea che finanzia i ricercatori di eccellenza che intendono svolgere attività di ricerca di frontiera negli Stati membri dell’UE o nei paesi associati. L’ERC supporta progetti di ricerca ad alto rischio, condotti da Principal Investigator (PI) con curriculum di rilievo a livello internazionale. I progetti sono finanziati sulla base delle idee progettuali presentate dai ricercatori, a loro volta valutati sulla base del solo criterio dell’eccellenza scientifica. I progetti ERC sono la linea di finanziamento della ricerca più prestigiosa a livello europeo.
L’ERC offre 4 schemi di finanziamento: Starting Grant, Consolidator Grant, Advanced Grant e Synergy Grant. Inoltre, un ulteriore schema, il Proof of Concept, aiuta i beneficiari a esplorare il potenziale di innovazione delle loro idee o dei risultati della ricerca.
Lo schema Synergy finanzia progetti così ambiziosi da richiedere un team che, per realizzare la ricerca e ottenere progressi sostanziali nelle frontiere della conoscenza, abbia la necessità di lavorare in sinergia condividendo risorse e unendo insieme competenze trasversali, interdisciplinari e complementari. Per questo si rivolge a gruppi costituiti da un minimo di due a un massimo di quattro Principal Investigator (PI). Il finanziamento può arrivare fino a 10 milioni di euro per singolo progetto, per una durata massima di 6 anni. Le proposte progettuali, che possono riguardare svariati ambiti, vengono valutate in base al solo criterio dell’eccellenza scientifica, intesa anche come sinergia e collaborazione tra persone diverse.
Alla base del progetto NEMESIS
Il progetto NEMESIS si colloca nell’ambito della matematica applicata e computazionale. Un modello matematico “physics-based” è una rappresentazione di un fenomeno fisico che utilizza, tra le altre, funzioni matematiche, equazioni e sistemi di equazioni alle derivate parziali per modellare uno specifico problema (ad esempio nell’ambito dell’ingegneria, delle scienze della vita e della terra). Tuttavia, data la complessità dei fenomeni fisici, i relativi modelli matematici non consentono sempre di scrivere esplicitamente la soluzione. È quindi necessario approssimare la soluzione tramite metodi numerici, cioè sostituendo il modello matematico con un algoritmo, costituito da una sequenza di istruzioni composte esclusivamente da un elevatissimo numero di operazioni elementari (come addizione e sottrazione) che vengono poi eseguite da un (super) calcolatore.
La matematica numerica svolge un ruolo fondamentale nella progettazione degli algoritmi, e nella loro analisi teorica e della complessità computazionale. Inoltre, i problemi di interesse in contesti reali dell’ingegneria e delle scienze applicate sono spesso caratterizzati da una complessità sia del fenomeno fisico (ad esempio la coesistenza e la mutua interazione di diverse variabili fisiche su scale spazio/temporali molto diverse) che del dominio di calcolo (ad esempio, la presenza di migliaia di microstrutture, mezzi fortemente eterogenei e geometrie mobili). Tutte queste caratteristiche devono essere opportunamente ed efficientemente gestite da un metodo numerico.
Un nuovo paradigma: i metodi politopali
Attraverso un lavoro di squadra e sinergico, in NEMESIS abbiamo come obiettivo ambizioso lo sviluppo di una nuova generazione di metodi numerici, in grado di superare le barriere attuali. Partiremo dalle basi teoriche fino all’implementazione su supercomputer (potenti sistemi di calcolo progettati per eseguire compiti intensivi, come simulazioni avanzate). Confidiamo di migliorare capacità predittive e prestazioni degli algoritmi con tecniche di intelligenza artificiale.
I metodi numerici classici, utilizzati per descrivere in maniera approssimata una legge fisica, come ad esempio i metodi agli elementi finiti, si basano sull’idea di suddividere il dominio fisico in volumi elementari (la cosiddetta griglia di calcolo o mesh). In questi metodi, poiché i volumi elementari possono essere costituiti solo da elementi di forma preassegnata (tipicamente, tetraedri, esaedri o prismi), il processo di generazione e gestione della griglia di calcolo può rappresentare il collo di bottiglia dell’intera simulazione al calcolatore, con costi (anche a livello di impatto ambientale) molto importanti. Per superare questa limitazione, negli ultimi anni sono stati sviluppati i metodi “politopali” [1,2,3,4] che supportano griglie di calcolo composte da elementi di qualunque forma (poliedri), superando quindi il paradigma classico.
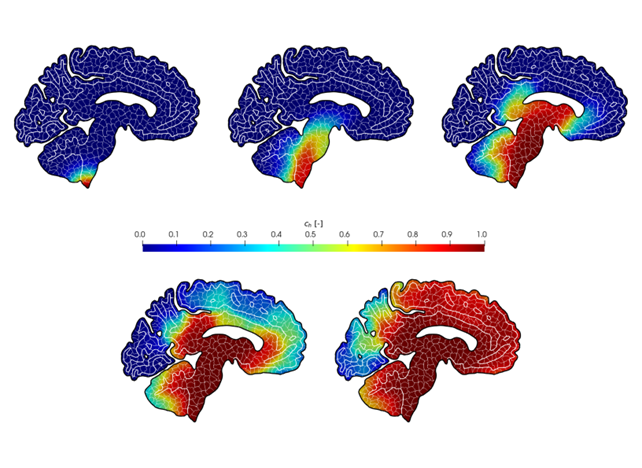
Figura 1. Mesh poligonale di una sezione di cervello nel piano sagittale e simulazione della concentrazione ch di proteina alfa-sinucleina nella malattia di Parkinson in un arco temporale di venti anni (https://brainum.mox.polimi.it).
Tra le principali innovazioni dei metodi politopali ci sono un’eccezionale capacità di approssimazione dei dati e del dominio di calcolo, l’integrazione diretta di leggi fisiche specifiche nell’ambito numerico (che consente di rispecchiare la reale struttura del problema fisico in esame) e una notevole efficienza nell’elaborazione computazionale.
Io, Lourenco Beirao da Veiga, Daniele A. Di Pietro e Jérôme Droniou collaboriamo allo studio dei metodi politopali sin dalla loro nascita. Abbiamo una storia decennale di collaborazioni alle spalle sia nell’ambito di progetti di ricerca che nell’organizzazione di eventi scientifici. Abbiamo tutti una formazione da analisti numerici, ma con caratteristiche complementari. Solo assieme potevamo coprire lo spettro delle conoscenze richieste per il progetto NEMESIS: dall’analisi teorica e numerica delle PDEs fino al calcolo scientifico e alle applicazioni, passando per le tecniche di intelligenza artificiale.
La costruzione della squadra è stata così molto naturale. Eravamo tutti esperti riconosciuti di metodi politopali, ma sufficientemente diversi da completarci a vicenda. C’erano tutti gli elementi per costruire un progetto così ambizioso da non poter essere svolto da un unico ricercatore, ma con la collaborazione sinergica fondata sulla fusione di competenze diverse, esattamente come richiesto dai bandi ERC SYNERGY grant.
Nel progetto NEMESIS svilupperemo un rigoroso quadro matematico formale e algoritmi efficienti per abilitare questo nuovo paradigma computazionale in contesti applicativi. Tutte queste caratteristiche distintive potranno avere un ruolo chiave nella costruzione di modelli physics-based (che sfruttano cioè conoscenze a priori come le leggi fisiche e che incorporano in modo innato i concetti di spazio, tempo e causalità) e di algoritmi efficienti e sostenibili.
Le prospettive del progetto NEMESIS
Nel progetto NEMESIS affronteremo inoltre la sfida di abilitare i metodi politopali in applicazioni rilevanti in tema di sostenibilità. Ad esempio, ci occuperemo di studiare problemi di mitigazione degli effetti delle attività antropiche nel sottosuolo, come la costruzione di scenari virtuali per prevedere gli effetti degli stoccaggi di CO2 o della produzione di energia geotermica (Figura 2). Ancora, ci occuperemo dello studio delle equazioni della magnetoidrodinamica (MHD)[5]. Si tratta di equazioni che descrivono la dinamica dei fluidi elettricamente conduttori in presenza di un campo magnetico. I modelli computazionali basati sulle equazioni dell’MHD sono un laboratorio virtuale unico dove poter testare, tra gli altri, i complessi meccanismi della fusione termonucleare controllata, ma anche i processi (ad alta energia) di produzione dell’alluminio. I metodi numerici politopali per risolvere le equazioni MHD potranno quindi essere utilizzati per ottimizzare i processi di produzione, acquisendo una conoscenza dettagliata della complessa fisica che c’è dietro.
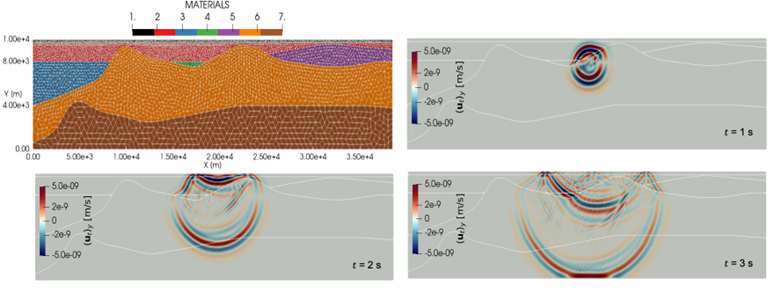
Figura 2. In alto a sinistra viene mostrata la griglia computazionale costituita da 4870 poligoni rappresentante la sezione verticale di un modello crostale di terreno. Colori diversi rappresentano materiali con diverse proprietà meccaniche. Viene inoltre riportato la velocità verticale del campo d’onda calcolato a diversi istanti di tempo: t = 1s (alto a destra), t = 2s (basso a sinistra) e t = 3s (basso a destra). Lavoro in collaborazione con Ilario Mazzieri, Michele Botti e Stefano Bonetti.
Gran parte delle risorse del progetto NEMESIS verrà utilizzata per formare giovani ricercatrici e ricercatori, sia a livello dottorale che post-dottorale. Prevediamo di aprire per loro 23 posizioni, per un totale di 75 anni circa di borse di ricerca. Al progetto collaboreranno, comunque, colleghi più senior, già strutturati e con esperienza alle spalle.
Referenze
[1] Antonietti, P. F., Facciola, C., Houston, P., Mazzieri, I., Pennesi, G., & Verani, M. (2021). High–order discontinuous Galerkin methods on polyhedral grids for geophysical applications: seismic wave propagation and fractured reservoir simulations. Polyhedral Methods in Geosciences, 159-225.
[2] Antonietti, P. F., da Veiga, L. B., & Manzini, G. (Eds.). (2022). The virtual element method and its applications (Vol. 31). Springer Nature.
[3] Beirão da Veiga, L., Brezzi, F., Cangiani, A., Manzini, G., Marini, L. D., & Russo, A. (2013). Basic principles of virtual element methods. Mathematical Models and Methods in Applied Sciences, 23(01), 199-214.
[4] Di Pietro, D. A., & Droniou, J. (2020). The Hybrid High-Order method for polytopal meshes. Number 19 in Modeling, Simulation and Application.
[5] Gerbeau, J. F., Le Bris, C., & Lelièvre, T. (2006). Mathematical methods for the magnetohydrodynamics of liquid metals. Clarendon Press.