All’inizio di dicembre è uscito su Nature “Advancing mathematics by guiding human intuition with AI” di Davies, Velickovic, et al.[1 ]Davies, A., Velickovic, P., Buesing, L., Blackwell, S., Zheng, D., Tomasev, N., Tanburn, R., Battaglia, P., Blundell, C., Juhasz, A., Lackenby, M., Williamson, G., Hassabis, D., & Kohli, P. (2021). Advancing mathematics by guiding human intuition with AI. Nature, 600(7887), 70-74. https://doi.org/10.1038/s41586-021-04086-x. In questo articolo si annuncia un nuovo traguardo per l’intelligenza artificiale. In poche parole, un team formato di matematici e informatici di DeepMind sarebbe riuscito a usare delle tecniche di machine learning per arrivare a nuove scoperte in teoria dei nodi e in teoria delle rappresentazioni. L’intelligenza artificiale avrebbe quindi fatto un bel passo avanti visto che la matematica restava un dominio (ormai tra i pochi in campo scientifico) in cui non trovava ancora applicazioni. Silvia De Toffoli ci racconta meglio questa storia.
DeepMind ha già ottenuto risultati sorprendenti con l’uso dell’intelligenza artificiale non solo nel dominio dei giochi ma anche in quello della biologia. Nel 2015 AlphaGo è stato il primo programma in grado di vincere contro un campione di Go e nel 2017 è stato lanciato AlphaZero, un programma che ha imparato a giocare “da solo”, senza analizzare un data set di partite già giocate. AlphaZero ha battuto campioni mondiali di Go, shogi e scacchi. Risultati strabilianti. In biologia, verso la fine del 2020 AlphaFold è stato in grado di predire con un’accuratezza senza precedenti la struttura tridimensionale che le proteine ottengono attraverso il loro ripiegamento – quello di predire il ripiegamento delle proteine è un problema importantissimo in biologia e il risultato del team di DeepMind rappresenta una rivoluzione in campo medico e biologico.
Ma la matematica è un caso a parte. Non è una scienza empirica come la biologia, e non ha uno scopo così ben definito come il Go o gli scacchi. Certo, vogliamo dimostrare nuovi risultati, scoprire nuovi teoremi, ma non tutte le possibili proposizioni matematiche sono egualmente interessanti o profonde. La matematica è ostica all’intelligenza artificiale. La notizia di questa nuova applicazione ha quindi subito generato una miriade di reazioni e suscitato ottimismo per il futuro.
La novità non consiste però nell’usare i computer in matematica, questo si fa già da molti decenni, ma nell’usare tecniche specifiche di IA. L’uso dei computer in matematica risale agli anni ’70, quando Apple e Haken hanno creato la prima dimostrazione assistita da computer. Si tratta della dimostrazione che ha finalmente trasformato la congettura dei 4 colori nel teorema dei 4 colori[2 ]La storia di questa congettura è molto affascinante. Nel 1879 Kempe aveva pubblicato quella che riteneva essere una dimostrazione; questa fu accettata e la congettura considerata risolta. Ma nel 1890, 11 anni più tardi, Heawood trovò una configurazione del problema che non era stata considerata dalla dimostrazione di Kempe.. I computer sono anche molto usati per creare modelli matematici e generare e testare insieme di dati strutturati. C’è anche un intero giornale scientifico dedicato esclusivamente a questo tipo di matematica sperimentale, Experimental Mathematics. Inoltre, i computer sono usati per controllare la correttezza delle nostre dimostrazioni. Attraverso gli assistenti di dimostrazione interattivi, partendo dalle loro prove informali, i matematici possono creare delle prove formali che vengono testate in maniera automatica. Per esempio, nel 2004 Gonthier[3 ]Gonthier, Georges (2008), “Formal Proof—The Four-Color Theorem” (PDF), Notices of the American Mathematical Society, 55 (11): 1382–1393 creò una prova formale proprio del teorema dei 4 colori. Recentemente, un gruppo di matematici e informatici è riuscito a ottenere in tempistiche sorprendenti una formalizzazione di un risultato recentissimo usando il software Lean[4 ]Si tratta del Liquid Tensor Experiment. Peter Scholze, medaglia Fields, ha lanciato una sfida alla comunità di Lean: formalizzare una sua dimostrazione. In circa 6 mesi il gruppo di Lean, guidato da Johan Commelin, è riuscito nell’impresa. I dettagli sono online nel blog di Kevin Buzzard: https://xenaproject.wordpress.com..
Ma questo nuovo risultato di Davies, Velickovic, et al. sembra aver raggiunto un nuovo traguardo in quanto prodotto con nuovi metodi di machine learning, metodi che potenzialmente potrebbero cambiare il modo di fare matematica. Nell’articolo di Nature si afferma che l’intelligenza artificiale ha la capacità di “guidare l’intuizione dei matematici” e può “aiutare nella scoperta di teoremi e congetture.” Ma in cosa consiste esattamente questo aiuto? E, cosa ancora più importante, questo aiuto potrebbe essere anche dato da metodi statistici tradizionali o è davvero qualcosa di esclusivo? Ci sono opinioni contrastanti a riguardo.
Per cercare una possibile risposta a queste domande, dobbiamo andare a vedere di che cosa si tratta: i risultati sono due, uno in teoria dei nodi e uno in teoria delle rappresentazioni. Senza entrare nei dettagli, cercherò di dare un’idea del primo problema.
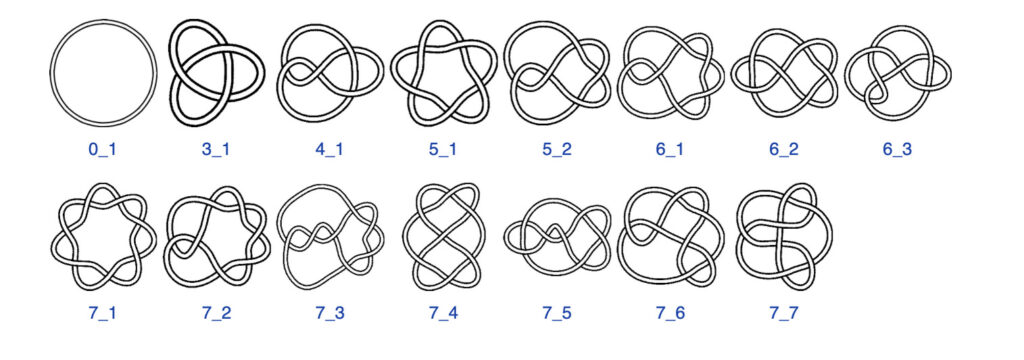
I nodi matematici sono delle astrazioni dei nodi fisici fatti con lo spago o con le spighette delle scarpe. I nodi matematici però, a differenza della maggior parte dei nodi fisici, sono chiusi, quindi dobbiamo immaginarci uno spago annodato con gli estremi incollati. Inoltre i nodi matematici non hanno spessore, ma sono curve nello spazio (e quindi hanno dimensione uno). In teoria dei nodi non ci interessiamo in generale alla forma geometrica di un nodo, ma del modo in cui esso è annodato. Quindi, più che i nodi, ci interessano i tipi di nodi. Dato un nodo particolare, possiamo muoverlo a piacere (attraverso delle isotopie ambiente) senza tagliarlo e rincollarlo, in modo da ottenere altri rappresentati dello stesso tipo di nodo. Nella figura sottostante ho riportato i (tipi di) nodi che ammettono un diagramma con un massimo di 7 “crossings” (si tratta dell’inizio della tavola dei nodi presente in Rolfsen, 1976[5 ]Rolfsen, D. (1976). Knots and Links. American Mathematical Society, Chelsea Publishing.).
Il problema principale in teoria dei nodi è catalogare i nodi e distinguerli gli uni dagli altri. Ci sono tanti modi per farlo, ma il modo privilegiato è quello di ricorrere a degli invarianti, che possono essere pensati come delle proprietà matematiche che associamo a dei nodi particolari. La caratteristica principale è che se associamo due invarianti a due nodi, se i nodi sono dello stesso tipo, anche gli invarianti saranno equivalenti.
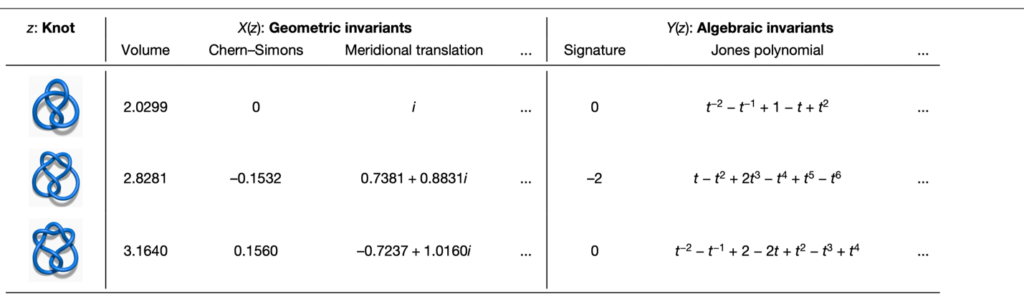
Ci sono due classi principali di invarianti di nodi, quelli algebrici e quelli iperbolici. Mentre gli invarianti algebrici sono oggetti matematici come gruppo e polinomi, gli invarianti iperbolici hanno a che fare con la struttura geometrica associata ai nodi. Queste due classi di invarianti vanno quindi a collegarsi con teorie matematiche molto diverse. Riporto qui una tabella dall’articolo di Nature di Davies, Velickovic, et al. con tre nodi e rispettivi invarianti:
Il team di ricercatori aiutato dall’IA è riuscito a definire una relazione tra queste due classi. Il nuovo concetto di “natural slope” è stato introdotto e la sua relazione con altri invarianti è stata dimostrata. I risultati matematici sono stati resi pubblici in un preprint su ArXiv (Davies, Juhász, et al., 2021)[6 ]Davies, A., Juhász, A., Lackenby, M., & Tomasev, N. (2021). The signature and cusp geometry of hyperbolic knots. preprint, ArXiv: 2111.15323.. Questa è una scoperta veramente significativa che probabilmente avrà numerose applicazioni e ramificazioni in teoria dei nodi e più in generale in topologia.
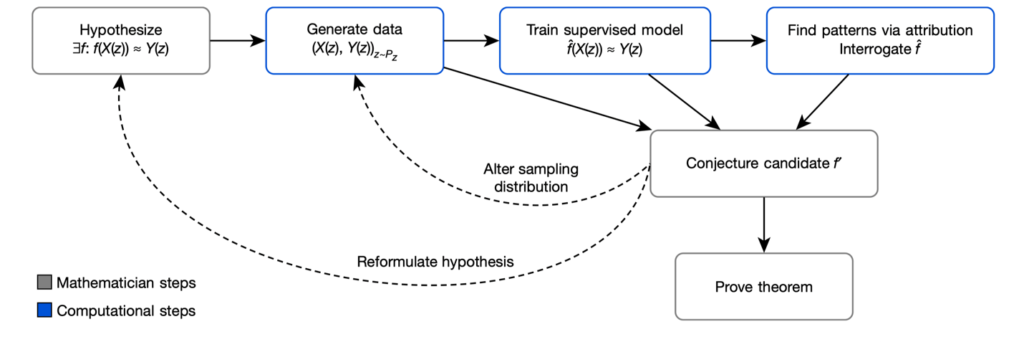
Ma qual è stato il ruolo dell’IA? Davies e gli altri autori dell’articolo di Nature propongono un framework per mostrare come l’IA abbia contribuito. Eccolo qui in forma schematica:
In pratica, l’IA può aiutare a raffinare l’intuizione dei matematici. Si parte comunque da un’ipotesi di lavoro. Nel nostro caso l’ipotesi è l’esistenza di una relazione tra invarianti algebrici e invarianti iperbolici di nodi. In generale l’ipotesi è l’esistenza di una relazione tra due quantità X(z) e Y(z) associate a qualche oggetto matematico z. L’IA ha sostanzialmente due ruoli: (1) verificare l’esistenza di tale relazione attraverso “supervized machine learning” e (2) usare tecniche di attribuzione per capire meglio questa relazione. In (1) si tratta di generare un data-set e usare la potenzialità del machine learning per testare varie funzioni che colleghino le due quantità. In (2) si tratta di raffinare l’ipotesi iniziale attraverso un processo iterativo. In parole povere, con questi strumenti i matematici possono prima testare e poi anche raffinare le proprie intuizioni. L’IA quindi non scopre nuovi risultati, ma è uno strumento che può in un certo senso aumentare il potere e la precisione del ragionamento intuitivo dei matematici. Ciò avviene attraverso un processo iterativo.
Ma non tutti sono dello stesso parere. Il matematico Ernest Davis (da non confondersi con il primo autore dell’articolo di Nature, Alex Davies) della New York University esprime scetticismo in un recente preprint[7 ]Davis, E. (2021). Deep Learning and Mathematical Intuition: A Review of (Davies et al. 2021). Preprint, ArXiv: 2112.04324.. Secondo Davis il ruolo dell’IA non sarebbe poi così centrale. La sua critica principale è che l’aiuto dato da queste nuove tecniche è simile all’aiuto che viene dato da metodi classici di analisi statistica. La critica è rivolta soprattutto al caso della teoria dei nodi, che è quello che ho discusso qui. Davis spiega: “Alla fin fine, il grosso del lavoro fatto dal deep learning è stato di isolare una relazione matematicamente semplice tra quattro parametri numerici reali.” Davis poi continua dicendo che nel caso della teoria delle rappresentazioni il ruolo dell’IA è più significativo, ma comunque non insostituibile.
È vero che qualsiasi nuova applicazione dell’intelligenza artificiale ottiene molto spazio mediatico e che si può tendere a esagerare il suo contributo. Resta però il fatto che questi sono dei nuovi risultati matematici significativi ottenuti attraverso la collaborazione di matematici e di esperti di machine learning. Bisognerà attendere nuovi risvolti per poter meglio valutare se l’IA sia davvero un salto drammatico rispetto a ormai collaudate tecniche usate in matematica sperimentale.
Note e riferimenti
| ⇧1 | Davies, A., Velickovic, P., Buesing, L., Blackwell, S., Zheng, D., Tomasev, N., Tanburn, R., Battaglia, P., Blundell, C., Juhasz, A., Lackenby, M., Williamson, G., Hassabis, D., & Kohli, P. (2021). Advancing mathematics by guiding human intuition with AI. Nature, 600(7887), 70-74. https://doi.org/10.1038/s41586-021-04086-x |
|---|---|
| ⇧2 | La storia di questa congettura è molto affascinante. Nel 1879 Kempe aveva pubblicato quella che riteneva essere una dimostrazione; questa fu accettata e la congettura considerata risolta. Ma nel 1890, 11 anni più tardi, Heawood trovò una configurazione del problema che non era stata considerata dalla dimostrazione di Kempe. |
| ⇧3 | Gonthier, Georges (2008), “Formal Proof—The Four-Color Theorem” (PDF), Notices of the American Mathematical Society, 55 (11): 1382–1393 |
| ⇧4 | Si tratta del Liquid Tensor Experiment. Peter Scholze, medaglia Fields, ha lanciato una sfida alla comunità di Lean: formalizzare una sua dimostrazione. In circa 6 mesi il gruppo di Lean, guidato da Johan Commelin, è riuscito nell’impresa. I dettagli sono online nel blog di Kevin Buzzard: https://xenaproject.wordpress.com. |
| ⇧5 | Rolfsen, D. (1976). Knots and Links. American Mathematical Society, Chelsea Publishing. |
| ⇧6 | Davies, A., Juhász, A., Lackenby, M., & Tomasev, N. (2021). The signature and cusp geometry of hyperbolic knots. preprint, ArXiv: 2111.15323. |
| ⇧7 | Davis, E. (2021). Deep Learning and Mathematical Intuition: A Review of (Davies et al. 2021). Preprint, ArXiv: 2112.04324. |









![Nodi da sciogliere - Episodio 1: Folletto, portali su e giù [Podcast] Episodio 1](https://maddmaths.simai.eu/wp-content/uploads/2025/01/Episodio-1-300x188.jpg)













