James Cass e Hermes Bloomfield-Gadêlha della University of Bristol hanno pubblicato su Nature Communications uno studio da cui emerge che la coda dello spermatozoo, il “flagello”, mentre si muove, genera schemi previsti da una teoria elaborata da Alan Turing negli anni Cinquanta. Il “pattern di Turing” è un’idea nata dalla teoria sui sistemi di reazione-diffusione e proposta dal matematico inglese per spiegare gli schemi ripetuti di forme e colori che osservabili in natura in animali, piante e non solo.

Interazioni tra sostanze chimiche creano pattern di Turing in numerosi casi, e concorrono alla creazione di una grande varietà di forme come spirali, strisce, macchie: si ritiene che la teoria di Turing abbracci formazioni comunissime in natura, che vanno dalle strisce delle zebre, alle spirali di semi nel disco di un girasole, alla disposizione della sabbia sulle spiagge.

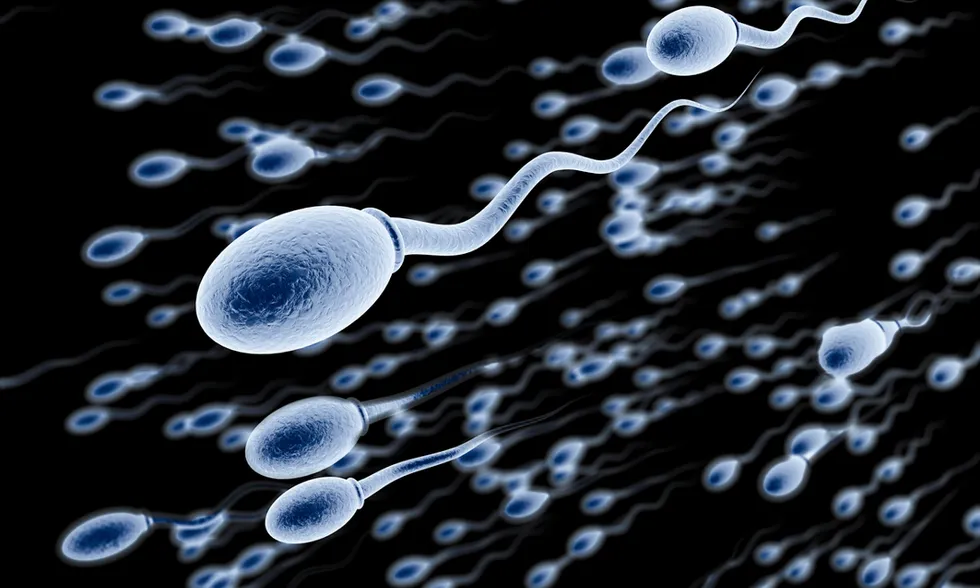
Il movimento del flagello di uno spermatozoo è estremamente complesso e coinvolge diversi fattori. Il ruolo del fluido esterno, in base ad alcuni recenti studi, sarebbe però di ben poco impatto. In questo studio, è stato esaminato questo aspetto mediante la simulazione al computer di una sorta di “gemello” digitale del flagello spermatico. Grazie anche al contributo di James F. Class del Polymaths Lab, i ricercatori hanno scoperto che i fluidi a bassa viscosità hanno un minimo effetto sulla forma del flagello. Questo significa che le ondulazioni nei flagelli si verificano praticamente in modo spontaneo, senza grande incidenza dell’ambiente acquoso, e che lo spermatozoo possiede un meccanismo infallibile che gli consente di nuotare in fluidi a bassa viscosità. Matematicamente, questo movimento spontaneo è equivalente al modo in cui sorgono i pattern nel sistema di reazione-diffusione di Turing (proposto per la prima volta per i pattern chimici).

La somiglianza tra schemi chimici e schemi di movimento è risultata sorprendente e inattesa perché, normalmente, non si pensa che i modelli chimici funzionino come i modelli di movimento (o di contrazione), né ci si aspetta che la matematica sia simile. “Ma ora che sappiamo che è così – spiega Bloomfield-Gadêlha – pensiamo che lo schema di movimento possa richiedere solo due semplici ingredienti: le reazioni chimiche che azionano i motori molecolari del flagello e la sua elasticità. Il fluido circostante ha un effetto minimo o nullo, negli ambienti acquatici”. Questi risultati potrebbero essere utilizzati in futuro per comprendere meglio i problemi di fertilità associati al movimento anomalo del flagello e la matematica alla base del processo potrebbe dare il via a nuove applicazioni robotiche, per esempio nei muscoli artificiali e nei cosiddetti “materiali animati”, ossia che sembrano “vivi” dato che cambiano la loro risposta a seconda di come vengono utilizzati.