Pochi giorni fa è stato dato l’annuncio del premio Abel 2024 assegnato a Michel Talagrand. In questo articolo Adriano Barra ci racconta che questo premio è legato in modo molto stretto alla scuola romana di meccanica statistica e sistemi complessi, dagli studi e teorie sviluppati negli anni da Giorgio Parisi fino al contributo matematico di Francesco Guerra.
Generalità sul premio e sul vincitore
Dal 2003 il premio Abel viene assegnato ogni anno dal Re di Norvegia per celebrare le migliori menti matematiche e allo stesso tempo ricordare il grande matematico norvegese Niels Henrik Abel (1802-1929). Nonostante l’idea di questo premio sia di vecchia data (venne infatti proposto alla fine dell’800, quando Norvegia e Svezia erano governate da Oscar II, Re di Svezia e di Norvegia, osservando che il premio Nobel in consegna a Stoccolma non copriva l’area matematica), nel 1905 l’unione tra Svezia e Norvegia si dissolse e questo impedì la messa a regime del premio per circa un secolo. Al momento, tra le 27 persone vincitrici del premio figura una sola donna, Karen Uhlenbeck, e il primo e l’ultimo dei vincitori condividono la nazionalità francese: nel 2003 il primo premio Abel viene assegnato a Jean-Pierre Serre (già Medaglia Fields e Premio Wolf) e adesso, nel 2024, a Michel Talagrand (già Loève Prize, Fermat Prize e Shaw Prize), in questo caso per i suoi vastissimi ed eterogenei contributi alla matematica e in particolare, prendendo a prestito le parole della Norwegian Acedemy of Science and Letters “for his groundbreaking contributions to probability theory and functional analysis, with outstanding applications in mathematical physics and statistics”.
Michel Talagrand, 68 anni, è un motore impressionante di risultati matematici di tutti i tipi, e, parafrasando le motivazioni fornite dall’Abel Committee, tra i suoi risultati di maggior rilievo troviamo l’approccio a largo spettro di metodi geometrici nei processi stocastici e nella probabilità, in particolare ad alta dimensionalità, dove le sue “concentrazioni di misura” rappresentano una maniera pulita, trasparente ed elegante, di razionalizzare un fenomeno che spesso euristicamente i fisici che lavorano in meccanica statistica chiamano “proprietà di auto-media delle osservabili”. Una descrizione della “concentrazione di misura”, per quanto possibile priva di tecnicismi, è fruibile a questo link dell’Accademia Norvegese e, semplifiando molto, possiamo dire che l’automedia è una proprietà statistica che permette di considerare solamente il valor medio di una variabile stocastica, garantendoci che le fluttuazioni che trascuriamo siano infinitesime nei limiti opportuni.
Le disuguaglianze di Talagrand sono citate nelle motivazioni del premio accanto ai suoi risultati su problemi di trasporto, che sono ad oggi di largo impiego in tanti scenari tra economia e finanza e ai suoi lavori fondamentali sui Processi Gaussiani. Tuttavia, a chiusura delle motivazioni del premio, un posto di grande rilievo è dato alla sua stima dell’energia libera del modello di spin glass di Sherrington-Kirkpatrick, la celebre “formula di Parisi”, che è stata alla base del Nobel a Giorgio Parisi (congiuntamente ad altri contributi miliari, e.g. la risonanza stocastica, solo per menzionarne uno). Ed è su quest’ultima motivazione che vogliamo soffermarci, sia per cercare di capirne l’importanza, sia perché – da una prospettiva storica – nasconde un’altra avventura in larga misura italiana, la storia della comprensione del fenomeno della “Rottura di Simmetria di Replica”.
Il “vetro di spin” (spin glass) come archetipo di un sistema complesso
È il 1975 quando David Sherrington e Scott Kirkpatrick scrivono un articolo, pubblicato dalla Physical Review Letters e intitolato “Solvable model of a Spin Glass” [1 ]Sherrington, David, and Kirkpatrick, Scott. “Solvable model of a spin-glass.” Physical review letters 35.26 (1975): 1792, dove descrivono un modello di sistema disordinato, all’apparenza molto semplice, ma le cui proprietà affascineranno una fetta ingente di scienziati per molto tempo. Questo modello descrive un sistema con delle variabili binarie (gli “spin” in gergo fisico, che possiamo immaginarci efficacemente come delle “frecce” che possono essere orientate solamente verso l’alto, “up”, o verso il basso, “down”, come in Figura 1) che interagiscono in campo medio (cioè ogni variabile risente dello stato di tutte le altre variabili in gioco, senza che vi sia introdotta una distanza tra loro: le variabili “lontane” non si sentono “meno” delle vicine) e le interazioni tra queste variabili possono essere o positive o negative. Un parametro di controllo reale positivo (la “temperatura” in gergo fisico) permette a queste variabili di influenzarsi sempre più (abbassando la temperatura) o sempre meno (alzandola).
Possiamo considerare prima il caso in cui le interazioni tra gli spin siano solo positive: questo descrive sistemi semplici, come i ferromagneti trattati da Curie e Weiss quasi un secolo prima, i quali esibivano una non sorprendente transizione tra una fase disordinata ad alta temperatura (in cui le interazioni tra gli spin non si avvertono e quindi una loro media campionaria -o “magnetizzazione” in gergo fisico- restituisce il valore zero) ed una fase ordinata a bassa temperatura (fase ferromagnetica) nella quale una semplice correlazione positiva (indotta da un’interazione positiva) tra tutte le variabili fa prediligere il loro orientamento verso uno dei due possibili stati, e.g. tutti gli spin allineati “verso l’alto” o “verso il basso” (come scegliere quale dei due casi non è importante in questo contesto), restituendo quindi una media campionaria del loro stato non più nulla. Questo tipo di interazioni semplici rende “soddisfatte” tutte le variabili poiché, come mostrato in Figura 1 (sinistra), nessuna “regola” viene violata, come discusso nella didascalia. Al contrario, in Figura 1 (destra) mostriamo un esempio di un vetro di spin: la differenza che balza all’occhio è che ora alcuni archi rappresentano interazioni negative, che quindi favoriscono coppie di spin anti-allineate (cioè con gli spin in senso opposto). Il fatto che in questo scenario ci siano interazioni positive (che favoriscono quindi l’allineamento degli spin, i.e. “up, up” o “down, down”) e interazioni negative (che favoriscono quindi l’anti-allineamento degli spin, e.g. “up” uno e “down” l’altro) rende la rete “frustrata” definendo il sistema “complesso” e quale sia l’ordine se la temperatura scema e si lasciano interagire queste variabili, non è più così intuitivo a predirsi.

Figura 1. Sinistra: esempio di sistema semplice (un ferromagnete di Curie-Weiss). Immaginiamo un grafo sui cui nodi mettiamo le variabili (e.g. gli spin, rappresentati come “frecce gialle” in queste reti in miniatura composte da soli tre nodi) ed i cui archi (rappresentati come “linee bianche”) rappresentano le loro interazioni. La rete nel suo complesso vuole cercare di disporre i suoi gradi di libertà (le frecce) in accordo con quanto suggerito dalle loro reciproche interazioni in maniera tale che, se queste sono positive (come contrassegnato dai “+” di fianco alle linee bianche), gli spin da esse connessi prediligono allinearsi, viceversa preferiscono anti-allinearsi se le interazioni tra loro sono negative (si veda l’immagine a destra). Nel caso in cui tutte le interazioni sono positive l’unica regola che emerge spontaneamente lasciando le variabili interagire, è che convenga loro scegliere se orientarsi tutte verso l’alto o tutte verso il basso (e quindi all’atto pratico correlarsi). Destra: esempio di sistema complesso (un vetro di spin di Sherrington-Kirkpatrick). La differenza con lo scenario precedente consiste nel permettere agli archi di rappresentare anche interazioni negative (graficate con linee rosse ed il segno “-“ di fianco): come le positive favoriscono l’allineamento tra gli spin, le negative favoriscono l’anti-allineamento. In questo caso si dice che la rete è “frustrata” poiché alcuni spin non possono simultaneamente soddisfare tutte le “regole” nelle quali sono coinvolti. Per esempio, se lo spin in basso a destra è “up” (come in figura) viola la regola in rosso, che coinvolge lo spin in alto, d’altronde se fosse “down” violerebbe la regola in bianco verso lo spin alla sua sinistra. Questo esempio ci lascia intuire come la ricerca di una disposizione ottimale di queste frecce, nel caso in cui siano tante e tutte connesse fra loro da metà archi bianchi e metà rossi, sia molto complicato.
Tale compito viene svolto dalla Meccanica Statistica, una branca della scienza (settore di lavoro di fisici teorici, probabilisti e fisici matematici in primis, ma non solo…) che si occupa di fornire una descrizione microscopica della materia che risulti in accordo con i Principi della Termodinamica nel momento in cui si considerano dimensioni macroscopiche di queste reti di spin. Semplificando molto, il fine di questa metodologia è di “ottenere un’espressione dell’energia libera del sistema oggetto di studio in termini di parametri di controllo, quali la temperatura, e parametri d’ordine, quali la magnetizzazione”. L’energia libera è la differenza tra l’energia del sistema e la sua entropia, a temperatura fissata, e la sua conoscenza permette di scoprire le varie fasi (ordinata/disordinata/etc.) che sono esplorabili dal sistema al variare dei parametri di controllo (ossia, alzando o abbassando la temperatura) semplicemente studiandone i minimi, poiché minimizzare l’energia libera vuol dire minimizzare l’energia e massimizzare l’entropia del sistema, cioè imporre che questo obbedisca ai Principi della Termodinamica. E così è stato anche per il vetro di spin. La chiusa dell’articolo di Sherrington e Kirkpatrick è il coperchio del vaso di Pandora che pochi anni dopo Parisi avrebbe iniziato a sollevare: “ci rendiamo conto che la soluzione che proponiamo non può essere sempre corretta poiché a temperatura nulla predice un’entropia negativa”. Questa cosa è però impossibile poiché l’entropia in quese reti conta logaritmicamente il numero di configurazioni accessibili alla rete di spin, quindi nel peggiore/migliore dei casi, in cui c’è un’unica disposizione – come per i ferromagneti tutti ordinati- l’entropia può diventare nulla, ma mai negativa.
La Meccanica Statistica Romana
Pochi anni dopo, in una serie di lavori diventati poi pietre miliari della scienza dei sistemi complessi, si veda per esempio nell’articolo del 1979 [2 ]Parisi, Giorgio. “Infinite number of order parameters for spin-glasses.” Physical Review Letters 43.23 (1979): 1754 (o direttamente nel libro [3 ]Mézard, Marc, Parisi Giorgio, and Virasoro, Miguel Angel. Spin glass theory and beyond: An Introduction to the Replica Method and Its Applications. Vol. 9. World Scientific Publishing Company, 1987), Giorgio Parisi dimostrò come aggirare il problema di Sherrington e Kirkpatrick e propose una soluzione che era tanto sbalorditiva quanto difficile da rende in forma di teorema matematico, almeno per l’epoca. La proposta di Parisi era che queste reti di spin, lasciate interagire con interazioni completamente casuali (metà positive e meta negative), spontaneamente si auto-organizzassero fino a formare un ordinamento gerarchico dei minimi della loro energia libera (e.g., come gli alberi tassonomici in Biologia o le strutture di vassallaggio nelle società feudali). Questa proprietà, nota in linguaggio tecnico come “ultrametricità”, era una naturale conseguenza della “soluzione di Parisi”, e veniva dall’espressione per l’energia libera che scaturiva dalla sua analisi e viene rappresentata stilizzata in Figura 2, dove confrontiamo la struttura dell’energia libera di un sistema semplice (senza frustrazione) e di un sistema complesso (con frustrazione).
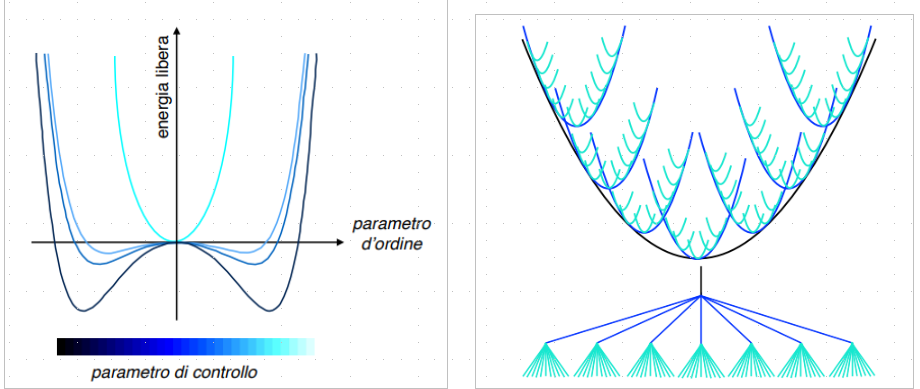
Figura 2. Sinistra: Rappresentazione grafica dell’energia libera vs la magnetizzazione (il parametro d’ordine) al variare della temperatura (il parametro di controllo) per il modello (semplice) di Curie-Weiss. Ad alta temperatura (graficata in celeste) l’energia libera è una parabola nella magnetizzazione ed è minima quando la magnetizzione è zero, mentre abbassando la temperatura l’energia libera (rappresentata da linee sempre più scure, dal blu al nero, nel grafico) diventa una quartica nel parametro d’ordine, sviluppando due nuovi minimi (simmetrici attorno a zero) a valori non nulli della magnetizzazione. Destra: Rappresentazione analoga per il modello (complesso) di Sherrington-Kirkpatrick. L’energia libera non ha più una forma liscia ed al diminuire della temperatura, la parabola grande (in nero) si decompone in una serie di altre parabole ricorsivamente gerarchizzate le une nelle altre (e rappresentate con colori diversi ad ogni livello di gerarchia): questo implica un ordinamento ultrametrico (“ad albero”) dei suoi minimi, come rappresentato nel sottostante.
Il problema però, più che chiudersi con quella soluzione, si apriva e questo per un intreccio di motivi. Il primo è che il modello di Sherrington-Kirkpatrick, anche se è forse difficile ritrovare in natura un sistema descritto esattamente dalla sua Hamiltoniana, in pratica approssima molto bene il comportamento di tantissimi fenomeni, dalle reti neurali, dove i neuroni vengono visti come elementi a due stati – alla stregua degli spin – e le connessioni tra essi sono mediate da sinapsi, alla complessità computazionale, alla fisica della materia amorfa, alla biologia evoluzionistica, in cui competono selezione e mutazioni casuali, alla proteomica e alle reti di regolazione geniche, oltre che a modelli sociali e molto altro. Già dagli anni ’80 dello scorso secolo era chiaro che comprendere a fondo il vetro di spin significava avere una chiave universale per interpretare un gran numero di fenomeni complessi, a prima vista lontanissimi tra loro, che venivano tutti raggruppati sotto l’ombrello della teoria di Parisi, nota tecnicamente come “rottura spontanea di simmetria di replica”.
L’altro motivo era invece squisitamente matematico: all’epoca l’unico metodo fruibile per trattare analiticamente questi oggetti era un metodo che aveva avuto origine nella fisica delle alte energie e poi importato nella meccanica statistica, conosciuto con il nome di “replica trick”. Questo procedimento non era, e non è, ben visto dai matematici che si sono dedicati con tenacia a “formalizzare delle alternative per la risoluzione dell’energia libera del vetro di spin”.
Nonostante contributi miliari di vari matematici, si veda per esempio [4 ]Aizenman, Michael, Lebowitz, Joel L. and Ruelle, David. “Some rigorous results on the Sherrington-Kirkpatrick spin glass model.” Communications in mathematical physics 112 (1987): 3-20 i progressi non sono stati molti fino ai primi anni duemila, quando Francesco Guerra (che, per curiosità aneddotica, aveva l’ufficio due stanze di fianco a quello di Giorgio Parisi presso il Dipartimento di Fisica di Roma Sapienza) produsse una serie di articoli illuminati (si vedano ad esempio [5 ]Guerra, Francesco. “Broken replica symmetry bounds in the mean field spin glass model.” Communications in mathematical physics 233 (2003): 1-12. e [6 ]Guerra, Francesco, and Toninelli, Fabio Lucio. “The thermodynamic limit in mean field spin glass models.” Communications in Mathematical Physics 230 (2002): 71-79, dove nell’ultimo lavoro compare come collaboratore anche Fabio Lucio Toninelli), nei quali gettava le basi per una costruzione alternativa – e matematicamente ineccepibile – per costruire la soluzione fornita da Parisi vent’anni prima, costruzione conosciuta come “l’interpolazione di Guerra”. Per comprendere l’importanza del lavoro di Guerra, anche nel guidare Talagrand a “chiudere il cerchio”, è utile uno sguardo alla Figura 3, dove riportiamo la prima pagina dell’articolo di Talagrand[7 ]Talagrand, Michel. “The Parisi formula.” Annals of mathematics (2006): 221-263, articolo in cui si dimostra un’altra limitazione per l’energia libera. L’altra era stata ottenuta da Guerra nell’articolo citato sopra del 2003, e quindi l’espressione di Parisi risultava stretta tra la limitazione di Guerra e quella di Talagrand.

Figura 3: prima pagina dell’articolo di Talagrand [7] dove l’altro bound -oltre quello di Guerra di [5]- per l’energia libera del modello di Sherrington-Kirkpatrick viene ottenuto esplicitamente. Si noti sia la dedica a Francesco Guerra che il metodo dichiarato nell’abstract del lavoro.
In realtà la storia del problema di Sherrington e Kirkpatrick non finisce con la dimostrazione della correttezza della formula di Parisi per la sua energia libera. Quello che rimaneva fuori -dalle stime di Guerra e Talagrand- era una dimostrazione rigorosa dell’ultrametricità: questa venne provata pochi anni dopo da Dmitry Panchenko[8 ]Panchenko, Dmitry. “The Parisi ultrametricity conjecture.” Annals of Mathematics (2013): 383-393 e, alla base della sua dimostrazione, si assumeva la validità di alcune identità, note come “identità ultrametriche”, che erano state dimostrate ante litteram (nel 1998!) anche loro da Guerra (con Stefano Ghirlanda)[9 ]Ghirlanda, Stefano, and Guerra, Francesco. “General properties of overlap probability distributions in disordered spin systems. Towards Parisi ultrametricity.” Journal of Physics A: Mathematical and General 31.46 (1998): 9149 ed estensivamente studiate dalla sua Scuola, per esempio in un articolo di Pierluigi Contucci (con Michael Aizenman)[10 ]Aizenman, Michael, and Contucci, Pierluigi. “On the stability of the quenched state in mean-field spin-glass models.” Journal of statistical physics 92 (1998): 765-783.
Conclusione
Lo stato attuale dell’arte è che il premio Nobel a Giorgio Parisi ed il premio Abel a Michel Talagrand sono il riconoscimento dovuto ad oltre quarant’anni di ricerca in meccanica statistica dei sistemi complessi e nelle sue sterminate applicazioni, e se da un lato è vero che finalmente abbiamo una teoria chiara ed esaustiva del modello di Sherrington-Kirkpatrick, le variazioni sul tema che ancora necessitano di controllo matematico sono sterminate. La speranza è che le nuove generazioni siano in grado continuare a far progredire questo approccio alla complessità e si affaccino nel mondo della ricerca scientifica nuovi Parisi, nuovi Guerra e, oggi più che mai, nuovi Talagrand. Certo, chi scrive (ed ha avuto Guerra come maestro, con il quale ha poi lavorato per quasi venti anni) non può non esprimere il suo rammarico nel non vedere il nome di Francesco Guerra comparire a fianco degli scienziati premiati, visto il ruolo cruciale che la sua ricerca ha avuto per trovare la via dietro infinite congetture. Ma, a parte questa constatazione personale, oggi è certo un’altra giornata di festa per il mondo dello spin glass e come tale intendiamo celebrarla invitando tutti a leggere il libro che Michel Talagrand ha scritto sui vetri di spin: un capolavoro della matematica moderna [11 ]Talagrand, Michel. “Spin glasses: a challenge for mathematicians. Cavity and mean field models”, Springer Press (2003).
Adriano Barra
Photo: Peter Badge / Typos1 / Abel Prize 2024
Note e riferimenti
| ⇧1 | Sherrington, David, and Kirkpatrick, Scott. “Solvable model of a spin-glass.” Physical review letters 35.26 (1975): 1792 |
|---|---|
| ⇧2 | Parisi, Giorgio. “Infinite number of order parameters for spin-glasses.” Physical Review Letters 43.23 (1979): 1754 |
| ⇧3 | Mézard, Marc, Parisi Giorgio, and Virasoro, Miguel Angel. Spin glass theory and beyond: An Introduction to the Replica Method and Its Applications. Vol. 9. World Scientific Publishing Company, 1987 |
| ⇧4 | Aizenman, Michael, Lebowitz, Joel L. and Ruelle, David. “Some rigorous results on the Sherrington-Kirkpatrick spin glass model.” Communications in mathematical physics 112 (1987): 3-20 |
| ⇧5 | Guerra, Francesco. “Broken replica symmetry bounds in the mean field spin glass model.” Communications in mathematical physics 233 (2003): 1-12. |
| ⇧6 | Guerra, Francesco, and Toninelli, Fabio Lucio. “The thermodynamic limit in mean field spin glass models.” Communications in Mathematical Physics 230 (2002): 71-79 |
| ⇧7 | Talagrand, Michel. “The Parisi formula.” Annals of mathematics (2006): 221-263 |
| ⇧8 | Panchenko, Dmitry. “The Parisi ultrametricity conjecture.” Annals of Mathematics (2013): 383-393 |
| ⇧9 | Ghirlanda, Stefano, and Guerra, Francesco. “General properties of overlap probability distributions in disordered spin systems. Towards Parisi ultrametricity.” Journal of Physics A: Mathematical and General 31.46 (1998): 9149 |
| ⇧10 | Aizenman, Michael, and Contucci, Pierluigi. “On the stability of the quenched state in mean-field spin-glass models.” Journal of statistical physics 92 (1998): 765-783 |
| ⇧11 | Talagrand, Michel. “Spin glasses: a challenge for mathematicians. Cavity and mean field models”, Springer Press (2003) |