\(\)

Apparso originariamente il 16 maggio 2017.

Matematica?!
Matematica, si.

Se vi state chiedendo cosa c’entri Salvador Dalí, uno degli artisti più visionari del suo tempo, con la matematica, provate intanto a dare un’occhiata ai baffi che sfoggia nelle fotografie della Figura 1: una qualche relazione si inizia a intravedere, no?

Figura 1: Forme matematiche nei baffi di Salvador Dalí.

Ma c’è molto di più: ammettiamo di voler sostenere che la matematica può essere, oltre che un valido supporto tecnico per gli artisti, anche un eccezionale stimolo creativo. L’opinione comune tende a essere piuttosto ostile al riguardo di un’affermazione di questo tipo. Analizzare l’opera di Salvador Felipe Jacinto Dalí y Domènech (1904-89), invece, è un ottimo modo per dare supporto a una tesi tanto spinta. A partire dalla sua affermazione, contenuta in Cinquanta segreti dell’artigianato magico, secondo la quale

«Devi, soprattutto da giovane, usare la geometria come guida alla simmetria nella composizione delle tue opere. So che i pittori più o meno romantici sostengono che queste impalcature matematiche uccidono l’ispirazione dell’artista, dandogli troppo su cui pensare e riflettere. Non esitare un attimo a rispondere loro prontamente che, al contrario, è proprio per non aver da pensare e riflettere su certe cose, che tu le usi».

Parafrasando, Dalí suggerisce al giovane artista una “ricetta” per la bellezza: fissa le proporzioni geometriche e poi lasciati andare, certo che il risultato sarà bello a vedersi. Questa ricetta è resa esplicita dai bozzetti preparatori di Dalí, uno tra tutti quello della Leda Atomica (fig. 2). Analizzando il dipinto con a fianco il bozzetto, ci accorgiamo infatti che nel quadro niente è lasciato al caso: il piede destro di Gala-Leda finisce in una delle cinque punte della stella pitagorica descritta dalle diagonali di un pentagono, inscritto nella circonferenza il cui diametro delimita la larghezza del quadro; la circonferenza è tangente in basso al basamento dello sgabello su cui è seduta Leda, e la testa della donna è interamente contenuta nella punta centrale della stella. «Certi giorni ho l’impressione che morirò di un’overdose di soddisfazione», diceva di sé. Deve averlo pensato a quadro finito: come contraddirlo?

Figura 2: Leda atomica (1949 – sin) e suo studio preparatorio (ds).

La Leda è uno degli esempi di quadri basati sul concetto di sezione aurea, che soggiace alla costruzione del pentagono: in un pentagono regolare, infatti, il rapporto tra ogni diagonale e il lato è uguale proprio a questo numero, $$\phi$$, noto nei secoli come numero aureo, numero d’oro, sezione aurea (i curiosi guardino qui  per saperne di più). Tutti gli artisti ne sono stati affascinati, e Dalí in questo è conformista: di rettangoli aurei e oggetti collegati la sua opera è infarcita anche quando non sembra.

È del tutto chiaro, per esempio, che il rettangolo aureo governa le proporzioni de L’ultima cena (fig. 3): la tavola si posiziona in modo da dividere l’altezza totale in due parti che stanno tra loro nel rapporto aureo; i discepoli alla destra e sinistra di Cristo dividono entrambi il quadro in due strisce verticali di ampiezze in rapporto aureo tra loro. Sullo sfondo compare poi il dodecaedro, che con le sue dodici facce pentagonali è un’incarnazione vivente del numero più elegante che esista.

Figura 3. Sezione aurea ne  L’ultima cena (1955)

Altrettanto esplicita è la presenza del numero $$\phi$$ in Mezza tazza gigante sospesa a un inesplicabile pendaglio alto cinque metri (1944 – fig. 4), di cui soprattutto ci pare irresistibile il titolo, col suo riferimento al pendaglio che serve solo per far tornare le dimensioni del quadro.

Figura 4: Spirale aurea in Mezza tazza gigante sospesa a un inesplicable pendaglio alto cinque metri

Ma quella della sezione aurea, se mi permettete, è una matematica di natura anche troppo popolare per uno come Dalí, che infatti estende il suo interesse a rami della matematica molto più elitari. Per esempio, nella mostra di Bologna potrete sicuramente apprezzare i daliniani orologi molli, resi celebri dal quadro La persistenza della memoria (Fig. 6 – sin). Si tratta di una raffigurazione della realtà che possiamo definire a pieno titolo topologica, con riferimento a una disciplina, la topologia, relativamente moderna. Si tratta di un tipo di geometria un po’ diverso da quello che si studia a scuola, quando tutti gli oggetti hanno le proprie misure, con contorni rigidi e indeformabili. Un topologo pensa invece agli oggetti come se fossero fatti di pongo (o Didò, o plastilina, a seconda del suo anno di nascita): due oggetti sono cioè topologicamente equivalenti se, pensandoli come fatti di plastilina, siamo in grado di deformare uno nell’altro senza effettuare tagli né incollamenti. Sono equivalenti, per esempio, un piatto piano, un piatto fondo e un bicchiere, mentre una tazzina con un manico non è equivalente ai primi, e una zuppiera con due manici non è equivalente né ai primi né alla seconda. La tazzina con un manico, invece, è equivalente a una ciambella, o a un donut (rigorosamente pronunciato come si scrive), come l’avrebbe forse chiamata Dalí, da bravo catalano (vedi qui).

I suoi orologi “colano” come se fossero fatti di plastilina, in una realtà in cui gli oggetti hanno contorni mutevoli, ma la loro memoria persiste e tiene traccia in qualche modo della forma. Sono topologiche, anche nel titolo, molte delle opere dell’ultimo periodo, come Contorsione topologica di una figura femminile (1983, fig. 5 – sin) e Contorsione topologica di una figura femminile che diventa un violoncello (1983, fig. 5 – ds)

Figura 5:  Contorsione topologica di una figura famminile (sin) e Contorsione topologica di una figura femminile che diventa un violoncello (ds)

Sarebbe imbarazzante, ancorché matematicamente significativo, entrare nei dettagli del conto del genere topologico della figura femminile rappresentata in questi due quadri, e forse qualcuno di voi invocherebbe un ricorso a Freud, peraltro ben presente in altre pagine di questo catalogo. Per questo mi autocensuro, e faccio invece un passo avanti, dalla topologia alla meccanica quantistica, destinato a farci lasciare Freud per Heisenberg, e gli orologi molli per la loro disintegrazione: come scrive Dalí nel suo Manifesto antimaterico, «durante il periodo surrealista volevo creare l’iconografia del mondo interiore e del mondo del meraviglioso concepiti da mio padre Freud. Oggi, invece, il mondo esteriore e quello della fisica hanno superato quello della psicologia. Oggi mio padre è il Dottor Heisenberg».
Di conseguenza, la persistenza del 1931 si disintegra nel 1954, scomponendosi in tasselli a riassumere il riconoscimento dell’autore per le nuove frontiere della scienza.

Figura 6: La persistenza della memoria (sin) e La disintegrazione della persistenza della memoria (ds)

Prima di abbandonare il concetto di topologia, guardatevi intorno nella mostra e riflettete sulle modalità dell’esposizione stessa: possiamo definirla in un certo senso “intrinsecamente topologica”, perché “cola” sulla città, in percorsi che esondano da Palazzo Belloni per investire tutta la città, in un’esperienza volutamente interattiva che ammorbidisce i confini, deformando e contaminando. Il che sicuramente a Dalí sarebbe piaciuto un sacco.

Ma andiamo oltre: se si parla del rapporto di Dalí con la matematica, non si può far a meno di accennare alla sua passione per la quarta dimensione, concretizzatesi nella bellissima rappresentazione dell’ipercubo che fa da scomoda croce al Cristo di Corpus Hypercubicus (1954 – fig. 7). Così come la croce rappresenta lo sviluppo piano di un cubo, la figura alla quale è inchiodato il Cristo daliniano rappresenta lo sviluppo tridimensionale del suo analogo in dimensione 4, che noi matematici chiamiamo appunto ipercubo: ciò serve all’artista per comunicare l’idea della trascendenza del Cristo, che vive in una dimensione superiore a quella che noi umani siamo capaci di concepire.

Vediamo di spiegare un pochino di che si tratta: tutti possiamo immaginare un quadrato. Se “stacchiamo” i due lati che convergono in uno dei suoi vertici, possiamo “aprire” il quadrato, fino a stenderlo lungo una retta, di cui occupa 4 segmenti consecutivi: questa figura rappresenta lo sviluppo 1-dimensionale di un quadrato, che di suo vive nel piano, ovvero in 2 dimensioni. Adesso prendiamo un cubo: tutti possiamo immaginarcelo, ma le cose sono ancora più facili se lo teniamo in mano, per esempio sotto forma di scatola cubica di cartone. Se tagliamo lungo tre lati consecutivi il tappo della scatola, e poi tagliamo accuratamente lungo altri lati (quali?) possiamo, analogamente con quanto fatto prima con il quadrato, “aprire” il cubo e spalmarlo sul piano di un tavolo: la figura a croce che otteniamo rappresenta lo sviluppo 2-dimensionale del cubo, che di suo vive invece nello spazio, ovvero in 3 dimensioni. Per finire, prendiamo un ipercubo: nessuno di noi se lo può immaginare (almeno credo, con gli artisti meglio non essere categorici) perché si tratta di un oggetto che vive in 4 dimensioni, dove la nostra percezione non ci consente di arrivare. Tuttavia possiamo pensare di fare l’analogo di quanto fatto prima col quadrato e poi col cubo, ovvero “tagliare” l’ipercubo lungo…lungo cosa?….pensateci, e concluderete che è lungo un insieme di quadrati, che fanno da bordo a cubi, che a loro volta fanno da bordo all’ipercubo. Se tagliate nel modo giusto, potete “aprire” il vostro ipercubo e “spalmarlo” …dove?…nello spazio ordinario, ovvero nello spazio a 3 dimensioni, dove tutti possiamo vederlo. Quello che vedremo è in realtà lo sviluppo 3-dimensionale dell’ipercubo, che di suo vive nello spazio 4 dimensionale, ma ci fa il piacere di lasciarsi spiaccicare in una dimensione inferiore, in modo che Dalí lo possa disegnare! Perplesso? Fai un salto qui

Catastroficamente creativo

e gioca con la quarta dimensione: ti piacerà!

Fig 7: Quarta dimensione in Dalí: Corpus hypercubicus (sin). Sviluppo di quadrato e cubo (ds)

Ma non è finita qui: qualunque turista, coi piedi gonfi e doloranti, pur se nel pieno del fervore culturale, a un certo punto sogna di fare una pausa e sedersi per riprendere le penne. Impossibile che non vi venga in mente di farlo, quando vedrete il giaciglio così invitante che fa bella mostra di sé in una delle sale centrali dell’esposizione bolognese (fig. 8). Decisamente è un divano. Ma certo non uno qualunque, con quel colore, rosso carminio, e soprattutto con quella forma.

Fig. 8 Divano Mae West (1935?) – in mostra

Del resto, visto che l’ha disegnato Lui, difficile aspettarsi un oggetto banale. Nel mio salotto starebbe benissimo, accanto alla porta finestra, anche se nessuna collocazione può eguagliare quella in cui il nostro uomo l’ha concepito, nella sua casa-museo di Figueres, a fare da bocca al volto un po’ serio dell’attrice Mae West. Ma la cosa che più sorprende è che questo oggetto, con la sua comoda sensualità, non si ispira (forse) alle labbra carnose di Gala né a quelle della stessa Mae West, bensì alla sensualità un po’ criptica di un … concetto matematico!

Concetto, tra l’altro, di quelli non proprio banali: quello di “singolarità”, o “biforcazione”, o “catastrofe”. A spiegarlo a Dalí possiamo immaginare sia il matematico René Thom, suo amico nonché medaglia Fields, autore del libro Stabilità strutturale e morfogenesi, la Bibbia delle catastrofi. Immaginiamo di avere un oggetto matematico, per esempio la curva di figura 2a, descritta da un’equazione contenente uno o più parametri. Facendoli variare con gradualità, i parametri possono essere usati come “manopole” per regolare la posizione e la forma della curva: talvolta piccole variazioni provocano altrettanto piccoli cambiamenti, come si può osservare passando dalla situazione di fig. 9a a quella di fig. 9b; in altri casi variazioni anche minime provocano la transizione fra due situazioni qualitativamente diverse, come il passaggio dalla curva fatta da un solo pezzo di figura 9b a quella composta di due pezzi di figura 9d. Si dice allora che è avvenuta una biforcazione, una catastrofe. Precisamente, la curva corrispondente alla catastrofe è quella di figura 9c, a partire dalla quale ogni minima perturbazione del parametro porta alle due situazioni qualitativamente diverse raffigurate nelle figure adiacenti. Thom nel suo libro classifica un numero finito di “catastrofi elementari”, dai nomi suggestivi quali coda di rondine, farfalla, piega, ombelico, che generano tutte le altre, tra cui la labbra di cui sopra.

Figura 9

Ora: se il libro di Thom presidia il comodino del nostro uomo a partire dal 1984, mentre il divano Mae West è del ’35, effettivamente è difficile che il secondo sia davvero ispirato al primo – anche se, essendo Dalí un visionario, non si sa mai. Immaginatevi però la soddisfazione di Dalí nel vedere il suo sofà emergere dalle pagine originali di Thom come “sezione della superficie continua di due cuspidi contenuta nell’immagine di catastrofe della coda di rondine”. Sembra uno scioglilingua, in effetti. Ma la figura 10 lo spiega con maggiore chiarezza.

Figura 10. Formazione della singolarità a labbra (da Tito Tonietti – sin), stessa singolarità nel libro di Thom (ds).

Se quella della singolarità a labbra è un’interpretazione a posteriori, non c’è dubbio che Dalí si ispiri esplicitamente alla teoria di Thom nelle sue ultime opere: la catastrofe nota come coda di rondine, per esempio, è protagonista sia del suo ultimo quadro, Coda di rondine e violoncelli (1983 – fig. 11, sin) che de Il ratto topologico di Europa. Omaggio a René Thom (1983 – fig. 11, ds).

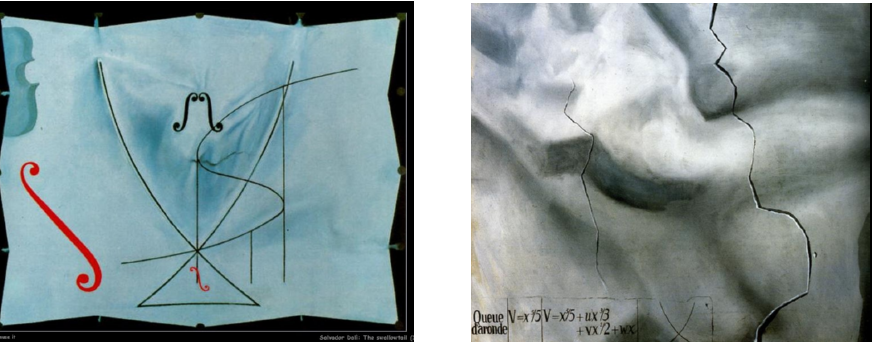
Figura 11: Coda di rondine e violoncelli (sin) e Il ratto topologico di Europa (ds).

D’altra parte, ormai anziano, l’artista definiva la Teoria delle Catastrofi «la più bella teoria estetica al mondo». E non si tratta di rincoglionimento senile: come abbiamo visto tramite molti esempi, Dalí è stato profondamente affascinato dalla matematica durante tutta la sua vita, e le sue opere riflettono in modo molto profondo questa passione.

Ma c’è molto di più: Salvador Dalí non solo della matematica capiva l’importanza, tanto da usarla rigorosamente nei suoi quadri, ma la studiava e ne conosceva un bel po’, grazie anche alla frequentazione di matematici importanti come René Thom, Matila Ghyka, Thomas Banchoff, Martin Gardner. Come del resto era irresistibilmente attratto da molte altre scienze: conosceva personalmente Einstein, aveva studiato teoria della relatività e fisica quantistica, la sua casa-museo pullula di modellini dell’atomo di idrogeno; la sua biblioteca conteneva centinaia di libri di scienza, con le sue annotazioni a margine a testimoniare la fervida lettura; fu fino alla sua morte abbonato a numerose riviste scientifiche; ormai anziano, non perse neppure una delle sei conferenze magistrali, di altrettanti importanti fisici, matematici, astrofisici e chimici, del simposio “Cultura y ciencia: determinismo e liberdad”, celebrato nel 1985 presso il suo museo; un suo quadro, in omaggio a Crick e Watson, si intitola Galacidalacidesoxiribonucleicacid… servono altre prove della sua fascinazione per QUALUNQUE scienza?

Ma limitiamoci alla mia (e vostra, sicuramente) disciplina preferita: una menzione sarebbe dovuta a mille altri temi, tra cui gli anamorfismi, la stereoscopia, le illusioni ottiche, gli ologrammi. Ma il campo degli argomenti matematici toccati da Dalí è talmente vasto che è inevitabile operare una selezione, democraticamente effettuata in base alle preferenze di chi scrive.

E quindi lasciatemi concludere con un argomento forse un po’ meno gettonato, ma di cui non potete non esservi accorti: l’ubiquità dell’uovo. Le uova in Dalí si trovano davvero ovunque: la cinta muraria della sua casa di Figueres (fig. 14) ne presenta di monumentali, sferiche o ovoidali; uova compaiono in moltissimi dipinti e sculture (per esempio la Venere in mostra); sono uova i volti di molte delle sue statue. Dalí evidentemente le considerava tanto fondamentali da utilizzarle anche come abitacolo per il suo ovocipede, peculiare mezzo di locomozione che ai suoi tempi non fu forse adeguatamente valorizzato, ma oggi costituisce la gioia di migliaia di bambini (tra cui il mio) e la disperazione di migliaia di mamme (tra cui la sottoscritta) quando lo incontriamo nei parchi gioco (fig. 12). Sia l’ovocipede daliniano che quello moderno, infatti, hanno un sistema propulsivo basato sul movimento del conducente, che sostanzialmente corre come un criceto facendolo girare, e uscendone poi mézzo di sudore, ma felice (almeno finché ha 8 anni…).

Fig. 12 Ovocipede daliniano e Ovocipede moderno

Per un topologo, un uovo è del tutto indistinguibile da una sfera (e anche da un cubo, o da un dodecaedro); inoltre, un uovo di struzzo è topologicamente equivalente a uno di quaglia, così come a un qualunque uovo di taglia intermedia. Se, però, dimentichiamo la topologia e consideriamo gli oggetti nel rispetto delle loro proprietà metriche, allora tutto cambia: l’uovo e la sfera sono oggetti distinti, e l’uovo di struzzo è metricamente diverso da quello di gallina. Quello che però accomuna uova di forme diverse è che tutte sono ottenute facendo ruotare una curva piana attorno al suo asse: se vogliamo ottenere una sfera faremo ruotare una circonferenza, se ci serve un ellissoide useremo un’ellisse, se invece vogliamo proprio un uovo…be’, la cosa si fa un po’ più complicata. Andate in frigo e prendetene uno qualunque: noterete che, se le sezioni effettuate con piani perpendicolari all’asse sono tutte circonferenze di diverse grandezze (il che ci dice che si tratta di una superficie di rotazione), quelle ottenute tagliando con piani che contengono l’asse non sono né circonferenze né ellissi, ma curve un po’ strane in cui c’è una parte più panciuta e una meno. Ovviamente un matematico non può cucinarsi un uovo alla coque ignorando l’equazione della curva che lo genera per rotazione: da qui le ovali di Cassini, Cartesio e Keplero, nonché l’uovo di Granville, quello di Hügelschäffer e quello di Moss, per finire addirittura col doppio uovo.

Fig. 13 Uova matematiche: di Cassini, di Granville, di Keplero, di Moss, doppio uovo.

Come dicevamo, Dalì con le uova è molto democratico: ne disegna e ne scolpisce di tutte le forme e misure, e viene spontaneo chiedersi perché. Una spiegazione possibile è che l’uovo è di fatto presente anche in molti dipinti classici, come simbolo di resurrezione, in quanto intrinsecamente legato alla nascita di una nuova vita: lo troviamo per esempio nella celeberrima Pala Montefeltro, detta appunto Madonna dell’uovo, di Piero della Francesca, che Dalí amava tanto da riprodurlo a modo suo nella famosa Madonna di Port Lligat (1950). È ben noto come Dalí provasse una profonda fascinazione per i classici, che reinterpretava in modi sempre non banali, per esempio facendo spuntare un paesaggio surrealista sulla guancia del Giuliano dei Medici di Michelangelo, o bucherellando strategicamente la sua riproduzione pittorica della Pietà. «Inizia a disegnare e a dipingere come gli antichi maestri» diceva in proposito. «Dopo potrai fare quello che vorrai: tutti ti rispetteranno».

Una seconda ragione per la persistenza dell’uovo nell’opera daliniana è probabilmente la sua teoria dell’uovo “intrauterino”: convinto di ricordare la sua vita all’interno dell’utero materno, lo trasforma in una specie di paradiso gastronomico dove imperano huevos fritos.

In maniera un tantino più prosaica possiamo anche vederci la manifestazione del suo spirito catalanista: a Barcellona e dintorni, infatti, l’ou si mangia in tutti i ristoranti, dalla bettolaccia al ristorante stellato, ferrat e accompagnato da patate e pernil de gla in versione popolare, oppure “cotto a bassa temperatura su parmentier di patata e spuma di butifarra negra” dalle 3 stelle in su. Del resto, è sicuro che Dalí abbia voluto rendere omaggio alla sua terra immortalandone alcune delle eccellenze culinarie: basti pensare alla pagnotta dell’Empordà con cui crivella le mura del suo palazzo (fig 14), e che tra l’altro con l’ou ferrat è la sua morte.

Figura 14. Uova e pagnotte nelle mura del Teatro Museo di Figueres

Del resto per Dalí, che a sei anni voleva diventare “cuoca”, la cucina è un piacere fondamentale, tanto da spingerlo a scrivere e illustrare perfino un libro di ricette, ovviamente “Le ricette di Gala”, evidentemente non proprio dietetiche se si legge nella prefazione: «Se tu sei un seguace di questi soppesatori di calorie che trasformano le gioie di un pasto in una punizione, chiudi il libro».

A questo punto è impossibile, anche se blasfemo, resistere alla tentazione di demistificare il nostro genio immaginandolo in ciabatte davanti a una tela ammezzata, mentre Gala col grembiulino spadella in cucina e a uova servite lo chiama: «Cariiiinyo, è in taaaavola, corri che ti si diacciaaa!» Bah…

Silvia Benvenuti

Per saperne di più

1. S. Benvenuti, Catastroficamente creativo: Salvador Dalí e la matematica, in AA.VV. Catalogo della mostra Dalí Experience, in: AA.VV (a cura di) Claudio Mazzanti, p. 56‐65, Bologna, Con-fine edizioni (2017).
2. S. Benvenuti, La sregolatezza regolata di Salvador Dalí, Mate giugno 2016, p.66-69.
3. G.I. Bischi, Biforcazioni, Lettera Pristem 100, 2016.
4. F. Blasco, Matemáticas en Dalí, Matematicalia vol 7, n. 4, 2011.
5. M. Cepeda Fuentes, Il surrealismo in cucina tra il pane e l’uovo, Il Leone Verde, 2004.
6. L. Chaparro, La obsesión de Dalí por una musa llamada ciencia, Sinc, 2013.
7. Salvador Dalí, Cinquanta segreti dell’artigianato magico, 1948.
8. M. Gardner, Anamorphic Art, in Time, Travel and Other Mathematical Bewilderments, W.H. Freeman, 1988.
9. R. Pérez Gómez, ¿Paranoia o topología trascendental? Salvador Dalí, 100 años, Gaceta de la RSME, vol 7.3, 2004.
10. C. Ruiz, Salvador Dalí y la ciencia, más allá de una simple curiosidad, Centro de Estudios Dalinianos. Fundación Gala-Salvador Dalí, Pasaje a la Ciencia pp. 4-13, 2010.
11. R. Thom, Stabilità strutturale e morfogenesi, Einaudi, 1980.
12. T. Tonietti, Catastrofi. Il preludio alla complessità, Bari, Dedalo, 2002.

Roberto Natalini

Roberto Natalini [coordinatore del sito] Matematico applicato. Dirigo l’Istituto per le Applicazioni del Calcolo del Cnr e faccio comunicazione con MaddMaths!, Archimede e Comics&Science.