Si allunga la vita media: in Europa siamo oltre gli 81 anni. Ma esiste un limite alla durata della vita? La matematica risponde per ora con il modello di Gompertz. Ce ne parla Marco Menale.
La vita media si sta allungando. O, per meglio dire, l’aspettativa di vita, almeno per alcune regione del mondo. Dai dati eurostat, al 2023 l’aspettativa di vita nell’Unione Europea è di circa \(81,4\) anni, con un incremento di \(0,8\) sul 2022, a conferma della ripresa dopo il periodo COVID. Anzi, abbiamo superato i livelli pre-COVID. Aumenta in giro per il mondo il numero di centenari. Ma, esiste un limite alla vita umana? O possiamo sperare, tra progressi e innovazioni, di prolungarla a piacere? Sembra di no, o almeno così stanno le cose secondo la legge di Gompertz.
Abbiamo già scritto in questa rubrica di Benjamin Gompertz, che è stato un matematico britannico, e della sua legge di crescita di popolazioni. Legge scritta proprio studiando e modellando l’aspettativa di vita delle persone per la valutazione delle polizze assicurative (beh, strane possono essere le strade del progresso).
Il modello è il seguente. Detto \(\mu(t)\) il tasso di mortalità di una popolazione a un’età \(t\), questo evolve come
\[\mu(t)=d_1e^{\alpha(t-t_1)},\]
dove \(d_1\) è il tasso di mortalità a un’età fissata, generalmente intorno (almeno) ai \(35\) anni, e \(\alpha\) è un parametro del modello. L’evoluzione è esponenziale, come ci si potrebbe (ma non vorrebbe) aspettare. In particolare, per alcuni valori di \(d_1\) e \(\alpha\) emerge che la probabilità di morire raddoppia ogni 7-10 anni circa. Ad esempio, se è dello \(0,2%\) intorno ai \(40\) anni, diventa dello \(0,4%\) intorno ai \(50\).
Nell’articolo del 2016 “Predictive implications of Gompertz’s law”, i ricercatori Peter Richmonda e Bertrand M. Roehner usano la legge di Gompertz per ottenere un limite dall’alto della vita umana. Fissato \(t_1=35\), con alcune manipolazioni derivano la relazione
\[\alpha=-0,0121\ln d_1 + 0.084.\]
Quest’ultima è stata verificata sia su dati trasversali, confrontando diverse nazioni in un dato periodo, sia su dati longitudinali, studiando l’evoluzione storica della mortalità in paesi come la Francia dal XIX secolo a oggi.
Dalla relazione precedente, usando i dati disponibili fino a un’età di \(106\) anni, i due ricercatori scrivono la relativa Gompertz per l’evoluzione del tasso di mortalità. Suppongono, qui, che la legge valga fino ai \(106\) anni e non oltre, data la scarsità statistica oltre questo valore, già enorme di per sé. Da queste premesse, ricavano il tasso di mortalità per la popolazione umana, con relative densità di probabilità e curva di sopravvivenza (Figura 1).
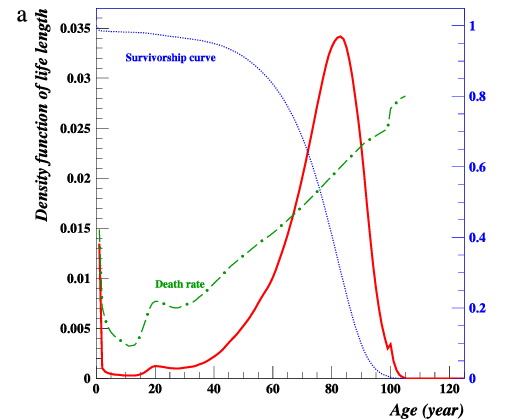
Figura 1. Le curve ricavate dalla Gompertz dell’articolo “Predictive implications of Gompertz’s law”: in rosso la probabilità di sopravvivenza, in blu la curva di sopravvivenza e in verde il tasso di mortalità.
Oltre quanto già prevedibile dalla legge di Gompertz, si vede come la curva si schiacci a zero dopo i \(100\) anni. A essere più precisi, collassa a zero a \(120\) anni: la probabilità di sopravvivenza collassa a zero giunti a questa (molto-veneranda) età. Si parla di “effetto muro” (dall’inglese, “wall effect”). Nemmeno stati molto popolosi come Cina e India dovrebbero avere individui che superano questa soglia più frequentemente rispetto a paesi con popolazioni molto più piccole. Ecco, almeno per questo modello, abbiamo un limite della vita umana.
Sebbene restino incertezze sull’esatta forma della curva per età superiori ai \(106\) anni, l’ipotesi che esista un limite naturale alla durata della vita umana sembra essere supportata dai dati empirici. Anche volendo migliorare i parametri del sistema, considerando, tra gli altri, i progressi della medicina degli ultimi anni (l’articolo a cui abbiamo fatto riferimento è del 2016), sembra che ci si debba rassegnare all’effetto muro. Ma, per ora, non prima dei \(120\) anni.




















Trackback/Pingback