L’expected goals (xG) misura la probabilità di trasformare in goal un’occasione di gioco. È uno dei numeri più utilizzati nel calcio. Il suo calcolo passa per la scelta di alcuni parametri, come l’angolo Kos. Ce ne parla Marco Menale.
I principali campionati di calcio stanno per terminare. Le coppe europee, come la Champions League, entrano, invece, nel vivo. Senza considerare il prossimo Campionato Europeo in Germania. È un continuo ricorso a numeri e dati, sia per analizzare quanto successo, che per fare analisi e previsioni. E l’expected goals (xG, in breve) è il capofila di questi numeri. L’xG misura con che probabilità un’azione di gioco si trasformi in goal. Una delle difficoltà è individuare i parametri che permettono questa stima. Tra questi c’è l’angolo Kos (Kos angle, in inglese).
In prima approssimazione l’xG di un’azione è calcolato con il valore atteso. Sia \(p\) la probabilità di fare goal (evento indicato con \(1\)) e \(1-p\) la probabilità di fallire l’occasione (evento indicato con \(0\)). Allora, l’xG dell’azione è
\[xG= 1\times p + 0\times (1-p)=p.\]
Dunque, l’xG coincide con la probabilità.
Stimare la probabilità di trasformare in goal un’azione non è semplice. Entrano in gioco tanti aspetti diversi, ed è difficile tener traccia di tutti. Ecco che bisogna individuare quei parametri che hanno un maggior peso nel calcolo dell’xG. Tra gli altri, ci sono la distanza dalla porta, \(d\), e l’angolo di tiro, \(\theta\) (in Figura 1). Nel primo caso, al diminuire della distanza, aumenta la probabilità di fare goal e, quindi, l’xG. Per l’angolo di tiro, l’xG aumenta con l’accentrarsi della posizione di tiro. E queste valutazioni sono in linea con quanto suggerito dall’esperienza.

Figura 1. L’angolo di tiro \(\theta\) a disposizione del calciatore in posizione \(A\). Fonte: Fonte: Karim, H., & Marwane, L. The Kos Angle, an optimizing parameter for football expected goals (xG) models. International Journal of Computer Science in Sport, 22(2), 49-61.
Come detto si tratta di prime approssimazione. Una stima più corretta richiede più parametri.
Supponiamo di voler migliorare la stima fornita dall’angolo di tiro \(\theta\). Quando un calciatore tira, difficilmente non ci saranno calciatori della squadra avversaria tra lui e la porta. A livello modellistico, significa considerare degli ostacoli lungo l’angolo di tiro, come mostrato in Figura 2.
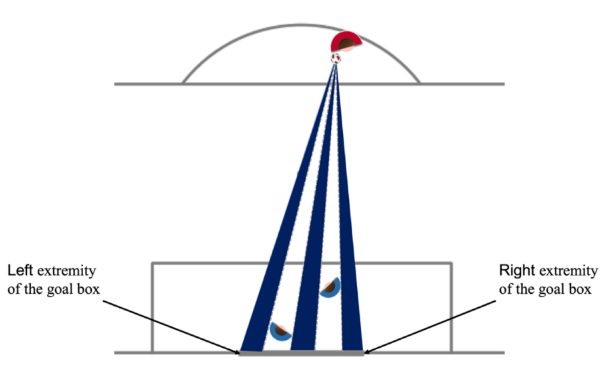
Figura 2. Calciatori avversari che occupano l’angolo di tiro. Fonte: Karim, H., & Marwane, L. The Kos Angle, an optimizing parameter for football expected goals (xG) models. International Journal of Computer Science in Sport, 22(2), 49-61.
Alcuni ricercatori hanno così introdotto l’angolo Kos, ossia una versione modificata dell’angolo di tiro che tiene conto della presenza dei calciatori avversarsi. I risultati sono presentati nell’articolo “The Kos Angle, an optimizing parameter for football expected goals (xG) models”.
Siano \(P_i\) i calciatori lungo l’angolo di tiro. Per ciascuno calciatore \(i\), si considera l’angolo \(\alpha_i\) che forma con le spalle rispetto alla linea di porta (Figura 3). Dunque, in questa nuova stima dell’xG si valuta l’orientamento del calciatore difendente rispetto alla linea di porta. Anche questa assunzione è motivata dall’esperienza. Infatti, un calciatore che sia con le spalle parallele alla linea di porta, ossia \(\alpha_i=0\) copre più angolo di tiro, rispetto a chi forma un angolo non nullo. Nel caso limite, con \(\alpha_i=90^°\), il giocatore è ortogonale alla linea di porta e copre pochissimo specchio. Con un po’ di geometria, si ottiene il valore dell’angolo Kos, assegnato l’angolo di tiro \(\theta\) e gli angoli \(\alpha_i\) (i più curosi trovano i dettagli matematici nell’articolo).

Figura 3. Il calciatore avversario \(P_i\) occupa l’angolo di tiro, con inclinazione \(\alpha_i\) della linea delle spalle rispetto alla linea di porta. Gli angolo \(alpha_i\) sono utilizzati per il calcolo dell’angolo Kos. Fonte: Karim, H., & Marwane, L. The Kos Angle, an optimizing parameter for football expected goals (xG) models. International Journal of Computer Science in Sport, 22(2), 49-61.
Definito l’angolo Kos, i ricercatori lo hanno utilizzato in algoritmi di machine learning (DTC, RFC e GBC) per stimare l’xG. In tutti i casi, i risultati hanno dimostrato che l’angolo Kos impatta nella stima dell’xG sia più dell’angolo di tiro che della distanza dalla porta. (Figura 4).

Figura 4: Impatto in percentuale dei vari parametri (angolo Kos, angolo di tiro, distanza e altri) nel calcolo dell’xG per i tre algoritmi di machine learning, DTC, RFC e GBC. L’angolo Kos ha il maggiore impatto in tutti e tre i casi. Fonte: Karim, H., & Marwane, L. The Kos Angle, an optimizing parameter for football expected goals (xG) models. International Journal of Computer Science in Sport, 22(2), 49-61.
L’angolo Kos rappresenta uno dei modi per migliorare la stima dell’xG. Si possono introdurre altri parametri. Ad esempio, si potrebbe tener conto del minuto della partita o del calciatore che tira. Tuttavia, questo significa complicare le formule di calcolo, con la necessità di algoritmi sempre più performanti. Serve quindi bilanciare i due aspetti, così da aver numeri sempre più realistici con cui goderci questa seconda parte di stagione.


















