Resoconto del terzo incontro del ciclo di seminari “ROAR IN AZIONE!”, su come la ricerca operativa possa essere applicata per la pianificazione e la gestione in tempo reale dei sistemi ferroviari.

Continuano gli incontri di “ROAR IN AZIONE!”, dedicati a presentare applicazioni della ricerca operativa e della matematica in generale, per affrontare e risolvere problemi di ottimizzazione emergenti in varie situazioni reali.

L’oratrice

Il terzo seminario è stato condotto da Veronica Dal Sasso, Operations Research Scientist  di OptRail s.r.l., azienda che fornisce soluzioni innovative di supporto alle decisioni per l’industria ferroviaria.

Veronica Dal Sasso.

Come è finita a occuparsi di sistemi ferroviari? Nella prima parte del seminario, Dal Sasso racconta di come sia stata la sua strada a “sceglierla”.

Alla fine del liceo scientifico, infatti, l’unica certezza che ha è il fatto che le piaccia molto la matematica, ma non vorrebbe né buttarsi nel mondo dell’insegnamento né rimanere in ambito accademico. Si iscrive perciò a Matematica presso l’Università di Padova, dove consegue prima una laurea triennale e poi una magistrale. Al termine dei cinque anni, il suo relatore le chiede se le va di fare un dottorato. Affascinata dall’idea, per sfidare un po’ la sorte fa domanda solo a Padova, dove riesce a entrare e a specializzarsi in matematica applicata, più precisamente in ricerca operativa. In seguito, ottiene anche una posizione da postdoc alla Lancaster University, nel Regno Unito. Lì, lavora al progetto “OptiFrame”, finanziato dall’Unione Europea, dove si studia un modo per centralizzare le decisioni sulle traiettorie degli aerei, tenendo in considerazione sia le richieste delle compagnie aeree sia le normative che regolamentano il traffico aereo. A inizio 2018 torna in Italia, inizia a cercare un altro lavoro, manda un curriculum a OptRail, e una decina di giorni dopo è assunta.

 

La matematica e i sistemi ferroviari

Perché una specialista matematica dovrebbe andare a lavorare in un’azienda che si occupa di sviluppare software per gestire dei treni?
I problemi da affrontare e risolvere in ambito ferroviario possono essere classificati in due categorie principali:

• pianificazione: riguardante tutto ciò che può essere deciso in anticipo (per esempio, come costruire il treno in termini di quanti e quali vagoni, il percorso dei singoli treni o l’orario delle fermate), in modo tale da ottenere un piano;
• gestione in tempo reale: relativo a tutto ciò che non è atteso (come gli imprevisti, i ritardi o gli incidenti di ogni genere), per capire come recuperare l’eventuale tempo perduto e soprattutto individuare quando il piano stabilito per i treni non è più valido e non può più essere eseguito perché potrebbe provocare, per esempio, una congestione.

Ci sono moltissimi fattori in gioco che potrebbero influenzare lo sviluppo (e la riuscita) dei piani progettati, così come la qualità delle loro soluzioni. E quale branca della matematica può aiutarci a valutare queste soluzioni, se non la ricerca operativa?

Durante il seminario, Veronica Dal Sasso ha approfondito due problemi di esempio, uno di pianificazione e uno di gestione in tempo reale. Introduciamoli e analizziamoli insieme qui di seguito.

 

Esempio di pianificazione: il Block Planning Problem

Consideriamo la rete ferroviaria degli Stati Uniti, mostrata nella figura sottostante.

Rete ferroviaria degli Stati Uniti (fonte: Map Attacks).

A differenza dell’Italia o di altri Stati europei, le ferrovie statunitensi sono prevalentemente usate per il trasporto delle merci. Date le grandi distanze e l’abbondanza di terre sconfinate, le persone per spostarsi preferiscono infatti ricorrere agli aerei.
La rete ferroviaria è divisa tra più compagnie che non solo operano i treni, ma sono anche proprietarie di quella parte di rete. Le stazioni in media sono molto piccole ma con molte piattaforme, le zone estese della rete sono a singolo binario, e i treni possono arrivare a essere lunghi anche tre chilometri.

 

La spedizione delle merci

In questo problema, consideriamo soltanto delle merci (o commodities) che entrano nella rete ferroviaria in alcuni punti particolari, chiamati yard. Ogni merce ha perciò un determinato yard di origine e un determinato yard di destinazione, dove uscirà dalla rete.
Chiaramente, tutto ciò che passa attraverso la rete deve essere gestito, considerando la numerosità degli yard e l’eterogeneità delle merci, che possono essere caricate in uno o più vagoni.

Nel video possiamo osservare le principali operazioni che avvengono in uno yard.

Come far sì che ogni merce raggiunga la propria destinazione finale? E come decidere su quali treni caricare le merci? Questo problema, essendo molto complesso, viene generalmente suddiviso in due fasi:

1. Raggruppamento di diverse merci e determinazione dei loro percorsi, individuando per esempio fino a quale yard intermedio più merci viaggiano assieme.
2. Assegnamento delle merci ai treni disponibili.

Rappresentazione di uno yard.

Uno yard è composto principalmente da:

• alcuni receiving tracks, ovvero i binari dove sopraggiungono i treni;
• un dislivello creato da una collinetta fisica, o hump, per far scendere i vagoni senza motrice verso i binari dove saranno raggruppati;
• alcuni classification tracks, ossia binari dove le merci vengono raggruppate in blocchi, a loro volta assegnati ai treni disponibili;
• i binari di pullout, dove i blocchi composti vengono caricati sul treno;
• un outbound track, corrispondente al binario di partenza del treno verso la rete ferroviaria.

Si ragiona quindi in termini di blocchi, assegnando loro una specifica origine (ossia, dove il blocco viene composto) e una destinazione (che può variare nel corso del tragitto).

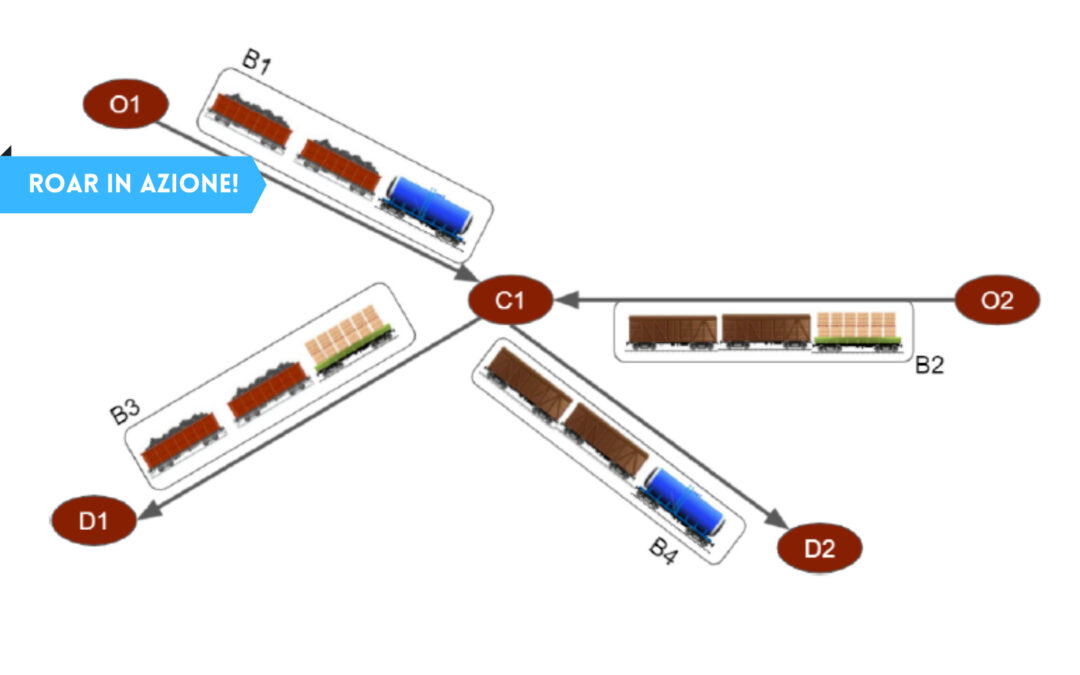
Da notare anche che la coppia origine/destinazione di un blocco può essere diversa dalle coppie origine/destinazione delle singole merci che compongono il blocco stesso. Infatti, i vagoni di un blocco viaggiano assieme per la durata del blocco, ma poi potrebbero essere riclassificati in alcuni yard intermedi, come succede nell’esempio in figura, nello yard C1.

Esempio: riclassificazione nello yard C1 dei vagoni dei blocchi B1 e B3,
che vengono scomposti per formare i nuovi blocchi B2 e B4. 

La riclassificazione è un processo molto costoso, perché tipicamente richiede un giorno di lavoro per la scomposizione e la ricomposizione dei blocchi, oltre che per il costo ulteriore della manodopera necessaria per rimescolare le merci. Per questo, meno operazioni di riclassificazione vengono programmate, meglio è.

Una soluzione banale potrebbe prevedere di assegnare ogni merce a un blocco esclusivo. Purtroppo gli yard hanno spesso una capacità limitata nel gestire i blocchi. Inoltre, si può formare un blocco che occupa più track, ma non più blocchi sullo stesso track. I blocchi quindi non devono essere “troppo piccoli”.

 

Formulazione del problema

Proviamo a formulare questo problema, chiamato Block Planning, attraverso un modello di programmazione lineare intera. Supponiamo innanzitutto che il flusso sia costante (ovvero, non ci preoccupiamo della dimensione temporale).

Funzione obiettivo

Si vogliono minimizzare i costi totali, composti da quelli di trasporto (le miglia percorse da ogni vagone) e da quelli di eventuali riclassificazioni. Solitamente, si equipara quest’ultima parte a 50 miglia aggiuntive per ogni vagone riclassificato. In questo modo, inoltre, le due componenti della funzione obiettivo hanno la stessa unità di misura.

Vincoli

Ogni blocco deve essere costituito da almeno un certo numero di vagoni (per esempio, cinque).
Ovviamente, si richiede che ogni merce raggiunga la sua destinazione finale.
Durante il percorso, la merce è assegnata a:

• un blocco solo, se non è coinvolta in processi di riclassificazione;
• più blocchi diversi, altrimenti.

Variabili

Per ogni merce e blocco, si introduce una variabile binaria che indica se quella merce è assegnata a quel blocco, avente una certa origine/destinazione.
Si può definire un grafo inserendo:

• un nodo per ogni yard nella rete;
• Un arco (A, C) per ogni blocco che ha origine in A e destinazione in C, avente come peso la distanza tra gli yard A e C.

Grafo di esempio.

Per ogni merce, vogliamo trovare un percorso sul grafo per sapere su quali blocchi viaggerà. Se due merci condividono parte del percorso, allora vuol dire che per quel tratto si trovano nello stesso blocco.

Raffinamenti

Al posto di specificare il numero minimo di vagoni per blocchi, si possono imporre condizioni alternative, quale per esempio quella uno yard, se esegue una riclassificazione, allora deve riclassificare almeno 150 vagoni.
Oppure si può anche pensare di minimizzare il numero di equipaggi da coinvolgere nelle operazioni.

Queste due varianti sono più difficili da modellare rispetto alla versione base descritta sopra: la prima richiede molti vincoli aggiuntivi, mentre la seconda modifica proprio la natura della funzione obiettivo.

 

Un piccolo esempio

 Istanza di esempio.

Nell’istanza in figura, vi sono quattro yard (A, B, C, D) e sei merci (C1, C2, C3, C4, C5, C6). I numeri vicino a ogni yard indicano il numero di classification track nello yard e la lunghezza del track. Per quanto riguarda le merci, è indicata la coppia origine/destinazione, il numero di vagoni e la lunghezza di ogni vagone.

Per esempio, lo yard A ha 3 classification tracks, lunghi ognuno 455.4 metri.
La merce C1, che parte da A e deve giungere in B, occupa 30 vagoni lunghi ognuno 18.8 metri, ovvero 564 metri in totale. Il blocco che conterrà la merce C1 dovrà quindi per forza occupare due track.
L’ultima merce in elenco, C6, occupa solo due vagoni. Nella soluzione ottima del modello di programmazione lineare intera, ci aspettiamo che non sia l’unica a occupare il blocco dove sarà assegnata.

Una volta implementato il modello, per esempio, con un linguaggio di modellazione algebrico come Mosel, si può sfruttare un risolutore per trovare una soluzione ottima.

Soluzione dell’istanza di esempio.

Le merci C1 e C2 viaggiano assieme nel blocco che ha origine in A e destinazione in B. In B, C2 viene riclassificata, componendo il blocco che contiene C2 stessa, C4 e C5, con destinazione C. C3 viene direttamente mandata in D in un unico blocco. In C avviene una seconda riclassificazione, componendo un ultimo blocco con C5 e C6, che raggiungono così la loro destinazione finale, ossia D.

 

Esempio di gestione di tempo reale: Dispatching

Una volta stabilito un piano, sulla carta ottimale, per tutti i treni nella rete, come far sì che le azioni effettive nella realtà aderiscano il più possibile a quanto schedulato? Come dicevamo all’inizio, possono infatti succedere imprevisti di varia natura. In tal caso, si decidono in tempo reale alcune azioni riparatrici, come il rerouting o il rescheduling. Tali decisioni vengono prese dai cosiddetti dispatchers. Più i dispatchers hanno esperienza, più sanno quali regole applicare per sistemare l’eventuale problema. Tuttavia, questa decisione manuale potrebbe rendere impossibile poi altri futuri passaggi. Per evitare questo, i dispatcher possono essere supportati da dei sistemi autonomi di traffic management.

Framework dell’OptRail Advanced Traffic Management System (ATMS).

Il software prende in input informazioni automatiche dal campo, più altri dati inseriti manualmente dai dispatchers. In base a essi, viene stabilito un nuovo piano, tradotto poi in azioni concrete da eseguire. Tutto questo viene ripetuto ogni dieci secondi. Considerato il brevissimo intervallo di tempo, l’algoritmo lanciato non si basa sulla risoluzione di un problema di programmazione lineare intera, ma sull’esplorazione di un albero di branching.

All’inizio, nel cosiddetto nodo padre, è chiesto di prendere una decisione (per esempio, dato un bivio, bisogna determinare in quale direzione prosegue il treno considerato). I nodi figli rispecchiano ognuno una delle possibilità, ovvero simulano gli effetti delle decisioni prese, e così via con altre generazioni di nodi per altre successive decisioni. Nei dieci secondi di tempo a disposizione, si esplorano le parti più promettenti dell’albero ottenuto e si sfruttano delle euristiche per ottenere la soluzione migliore in quell’intervallo (non per forza ottima). In questo caso, la funzione obiettivo per valutare la qualità delle soluzioni trovate punta a minimizzare il ritardo che le azioni riparatrici provocheranno, rispetto al piano in esecuzione. Tale ritardo è pesato con rispetto alle diverse priorità dei treni coinvolti.

 

La registrazione dell’incontro

Il video del seminario è disponibile qui:

 

Il prossimo incontro di “ROAR IN AZIONE!”

Il prossimo seminario sarà giovedì 10 marzo alle ore 11:00. La relatrice sarà Martina Fischetti (European Commission, Joint Research Centre), che presenterà alcune applicazioni della matematica nell’ambito della sostenibilità, tra energie rinnovabili e trasporti. Per poter seguire il seminario su Zoom, anche con un’eventuale classe di studenti, contattatemi via e-mail.