Ciao, l’altra volta abbiamo parlato di sequenze di monete, ricordi?
Sì, di cose che capitano a caso…
Oggi ho portato dei dadi, ti volevo far vedere un altro gioco basato sulla probabilità, abbiamo un po’ di tempo?
Non tanto, ti dovrei chiedere una cosa di geometria, ma se ci vuole poco…
Sì, sì, con un attimo te lo spiego.
Va bene…
Allora, disegno tre punti, i vertici di un triangolo… lo faccio equilatero per motivi di estetica

Vabbè, estetica…
Scelgo a caso un punto del triangolo.

Ok.
Tiro il dado:
se esce 1 o 2, scelgo il primo vertice;
se esce 3 o 4, scelgo il secondo vertice;
se esce 5 o 6, scelgo il terzo vertice.
Cioè scegli a caso un vertice. Decido io…quello in alto
Ok, poi disegno il punto medio del segmento che unisce vertice e punto vecchio.

Facile fin qui. Disegni un punto a metà strada fra un vertice, scelto a caso, e il vecchio punto, poi?
Poi basta, ripeti a oltranza tutto quanto: tiri il dado, scegli il vertice…
…segno il punto a metà strada fra vertice e punto trovato prima.

Sì, e se lo fai moltissime volte…

Mi sembrano solo un mucchio di punti messi a caso!
Si chiama gioco del caos infatti, ma continua.
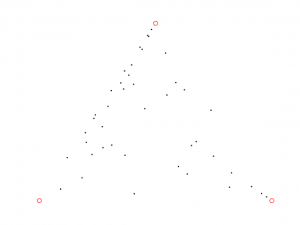
[Sussurra] Ma non doveva durare poco?…
[Dopo 500 punti]

[Dopo 1000 punti] Uff…

Ma… aspetta.
[Dopo 5000 punti] Wow! La conosco questa figura!

Si chiama triangolo di Sierpinsky.
Bello!
[Dopo 10000 punti]
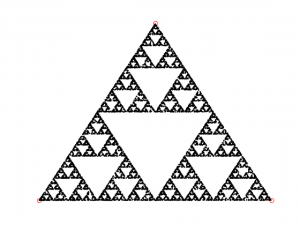
Hai visto? Anche scegliendo “a caso” il risultato… è ordine che viene dal caos!
Per me hai barato…
No, giuro! È una proprietà degli attrattori dei sistemi di funzioni iterate, sono frattali!
Se se, non inventare scuse, hai barato…



















