Una nuova mini-serie, fatta di video e articoli, di Alessandro Zaccagnini, matematico, esperto di teoria dei numeri, autore del Dialogo sui numeri primi. Questa volta si fa accompagnare da una tartaruga per raccontarci cosa sono le somme esponenziali e perché sono tanto utili nella sua disciplina. Questa è la prima puntata. Tutte le puntate le trovate su questa pagina.

Somme di vettori unitari con angoli razionali

Prendiamo il vettore unitario che dall’origine arriva nel punto di coordinate \((1, 0)\), lo ruotiamo di un angolo fissato, ripetiamo l’operazione e sommiamo uno dietro l’altro i vettori cosí ottenuti. Nell’immagine qui sotto vediamo in dettaglio le fasi della costruzione quando l’angolo di rotazione è di \(72^\circ\). Con il tratteggio rosso indichiamo le posizioni successive assunte dal vettore di partenza dopo 0, 1, 2, 3, …, rotazioni, mentre la linea nera indica le somme di 1, 2, 3, 4, …, vettori. Indichiamo anche il centro del poligono regolare che compare alla fine della costruzione, per un motivo che chiariremo piú avanti.

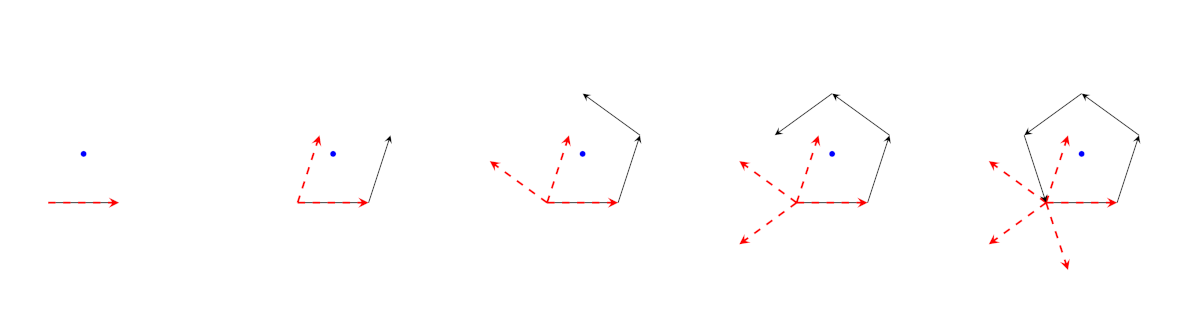
Le fasi della costruzione quando \(n = 5\)

Le figure che seguono illustrano i casi in cui l’angolo di rotazione vale \(120^\circ\), \(90^\circ\), \(72^\circ\), \(60^\circ\), \((360 / 7)^\circ\), \(45^\circ\), che corrispondono come vediamo ai poligoni regolari con \(n = 3\), 4, 5, 6, 7, 8 lati rispettivamente.

Nell’ambiente del logo che abbiamo menzionato nell’introduzione c’è una tartaruga alla quale possiamo dare sequenze di istruzioni che permettono di creare disegni molto complessi, come vedremo nelle puntate successive. Per fare un esempio, otteniamo il pentagono regolare con questa sequenza di istruzioni:

  Vai all'origine
  Guarda verso est
  Ripeti 5 volte
    Avanza di un passo
    Ruota di 72 gradi verso sinistra

La tartaruga è inizialmente nell’origine e guarda verso nord; nei comandi di rotazione si va sempre in senso orario, se l’angolo indicato è positivo, antiorario in caso contrario. Queste convenzioni sono diverse da quelle standard in matematica e quindi alcuni dei comandi che vedremo serviranno semplicemente a seguire le convenzioni.

Invitiamo i lettori ad aprire un emulatore del logo come per esempio quello che si trova all’indirizzo https://www.calormen.com/jslogo/# e provare a sperimentare da soli. Qui forniamo qualche esempio di funzioni in logo che permettono di disegnare tutte le nostre figure, procedendo gradualmente dalle piú semplici alle piú complesse che vedremo nell’ultima puntata.

to poligono :numero :lunghezza
   clearscreen
   showturtle
   setcolor pick [red]
   setheading 90
   make "angolo 360/:numero
   repeat :numero [
     fd :lunghezza
     setxy 0 0
     rt -:angolo
     wait 10]
   penup
   home
   setheading 90
   setcolor pick [black]
   pendown
   repeat :numero [
     fd :lunghezza
     rt -:angolo
     wait 10]
 end

 make "n 3
 repeat 10 [
   poligono :n 80
   make "n :n + 1
     wait 20]

definisci poligono :numero :lunghezza
  pulisci schermo
  mostra tartaruga
  prendi colore [rosso]
  scegli direzione 90
  poni "angolo 360/:numero
  ripeti :numero [
    avanza :lunghezza
    ponixy 0 0
    ruota -:angolo
    aspetta 10]
  solleva la penna
  torna all'origine
  scegli direzione 90
  prendi colore [nero]
  appoggia la penna
  ripeti :numero [
    avanza :lunghezza
    ruota -:angolo
    aspetta 10]
fine

poni "n 3
ripeti 10 [
  poligono :n 80
  poni "n :n + 1
     aspetta 20]

Definiamo in logo la funzione poligono, che genera una sequenza di :numero vettori di lunghezza :lunghezza, ciascuno ruotato di :angolo gradi in direzione antioraria rispetto al precedente, ed il poligono associato. Accanto, una traduzione in italiano dei comandi. La variabile :angolo è calcolata a partire dai dati in ingresso. I due cicli fanno essenzialmente la stessa cosa, ma nel primo si riporta la tartaruga nell’origine, senza cambiare la sua orientazione, dopo aver disegnato ciascun vettore (in rosso), mentre nel secondo caso lasciamo che la tartaruga vada avanti dalla posizione appena raggiunta (in nero). Le istruzioni wait permettono di osservare i movimenti della tartaruga, che altrimenti andrebbe troppo veloce! Nelle ultime righe chiamiamo la funzione poligono per disegnare in sequenza i poligoni regolari con 3, 4, …, 12 lati, con i vettori associati.

Alessandro Zaccagnini