Marco Ghimenti, matematico in forze al Dipartimento di Matematica dell’Università di Pisa, ci spiega perché l’ultimo film della Marvel sarebbe andato diversamente se il protagonista avesse avuto qualche nozione di analisi matematica.
Il film AVENGERS – Infinity War è stato un grande successo in tutto il mondo. È tratto dai fumetti della Marvel, la Casa delle Idee dove abitano personaggi popolarissimi come Spider-Man e gli X-Men e nel film ne compaiono letteralmente a decine. Il protagonista indiscusso è un cattivone come pochi: si chiama Thanos e non solo è davvero titanico ma è proprio un titano (nel senso – alla lettera – che proviene dall’omonima luna di Saturno) di nome. E qui non possiamo evitare uno spoiler, non proprio clamoroso, visto che Thanos persegue dichiaratamente i suoi scopi criminosi per tutto il film: alla fine metà degli esseri viventi dell’universo viene eliminata, cancellata, annichilita. Anche questo, alla lettera: a un certo punto tutti questi innumerevoli miliardi di esseri viventi smettono di esistere. Una soluzione decisamente drastica al problema della scarsità di risorse, che ha diviso il pubblico tra chi considera che in fondo Thanos non ha avuto tutti i torti e chi gli rimprovera di non avere pensato a soluzioni alternativa, come per esempio raddoppiare le suddette risorse (come potrebbe, con gli stessi poteri che gli permettono di fare quello che alla fine fa).

Ma un buon studente di Analisi, invece, dovrebbe uscire dal cinema con un’altra opinione: “Tanta fatica per nulla!”. Per sapere perché, ci vuole un pochino di pazienza, per entrare nel mondo della dinamica delle popolazioni e delle equazioni differenziali. Un’equazione differenziale è un’equazione che coinvolge una funzione incognita e le sue derivate. Ad esempio, pensiamo al numero di individui di una popolazione come ad una funzione che dipende dal tempo \(N(t)\). Il tasso di variazione di questa popolazione nel tempo è la derivata della funzione rispetto al tempo \(\frac{dN}{dt}\). Ovviamente la popolazione varia a seconda del numero di nascite e del numero di morti ad un certo istante, e possiamo immaginare che questa variazione sia proporzionale al numero di individui presenti: più individui ci sono, maggiori sono le probabilità di accoppiamento, e anche più individui ci sono, più individui muoiono in un certo istante. Possiamo immaginare quindi che il tasso di variazione sia direttamente proporzionale al numero di individui, moltiplicati per un fattore di natalità \(\alpha\), e un fattore di mortalità \(\omega\). Quindi otteniamo \[\frac{dN}{dt}(t)=\alpha N(t)-\omega N(t).\] Se consideriamo \(N_{0}\) il numero di individui all’istante iniziale \(t=0\) in cui cominciamo a considerare la nostra popolazione, l’equazione completa sarà \[\left\{ \begin{array}{l}
\frac{dN}{dt}(t)=\alpha N(t)-\omega N(t)\\
N(0)=N_{0}.
\end{array}\right.\] La soluzione di questa equazione, detta equazione di Malthus, è \[N(y)=N_{0}e^{(\alpha-\omega)t},\] quindi, se \(\alpha>\omega\) (ovvero se è più probabile fare figli piuttosto che morire) il numero di individui cresce esponenzialmente!
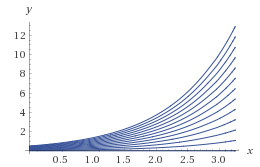
Fig.1 Curve delle soluzioni dell’equazione di Malthus di crescita della popolazione.
Ora, in questa equazione abbiamo fatto diverse semplificazioni: abbiamo considerato il numero di individui come una funzione reale e regolare, mentre gli individui sono un numero intero di persone. Questa però è una approssimazione molto ragionevole per popolazioni molto numerose. Poi abbiamo immaginato che il tasso di natalità e mortalità siano indipendenti sia dal tempo, sia dal luogo dove si trovano gli individui. Questo va bene per una colonia di batteri, ma non è molto adatto per le popolazioni umane: basta pensare alla differenza, ad esempio, tra India, Messico e Italia, o tra il numero di figli per famiglia e la durata di vita della nostra generazione rispetto a quella dei nostri nonni. Anche in questo caso, se consideriamo le cose su scala abbastanza vasta, come fa Thanos, può essere una approssimazione ragionevole.
Ma c’è una terzo fattore che a Thanos sta molto a cuore e che noi per adesso non abbiamo considerato: la scarsità delle risorse. La nostra popolazione è libera di riprodursi a piacimento, senza mai soffrire la fame. Se vogliamo convincere il nostro caro titano a non spazzare via metà universo, dobbiamo fornire un modello più convincente. Possiamo allora aggiungere una correzione negativa che sia piccola quando ci sono pochi individui, perché in quel caso l’effetto della scarsità di risorse è trascurabile, e che diventi molto grande al crescere del numero di individui. Il modello più semplice è prendere qualcosa che sia proporzionale al quadrato del numero di individui. La nostra equazione allora diventa \[\frac{dN}{dt}(t)=(\alpha-\omega)N(t)-\sigma N^{2}(t)\] dove più grande è il parametro \(\sigma\), più gli effetti della scarsità di risorse sono drammatici. Questa equazione, introdotta per la prima volta da Verhulst, è detta equazione logistica. Notiamo una cosa: la funzione costante \(N(t)\equiv\frac{\alpha-\omega}{\sigma}\) è una soluzione dell’equazione, infatti in questo caso \(\frac{dN}{dt}=0\) e \(\frac{\alpha-\omega}{\sigma}\) è una soluzione di \((\alpha-\omega)N(t)-\sigma N^{2}(t)=0\). Questa soluzione si chiama di equilibrio, infatti se partiamo con \(\frac{\alpha-\omega}{\sigma}\) individui all’istante iniziale, questo sarà esattamente il numero di individui per tutto il tempo. Ma la cosa più stupefacente è che tutte le soluzioni di questa equazione si avvicinano, indipendentemente dal numero di individui iniziale, proprio a questa soluzione speciale, come si vede in figura 2.
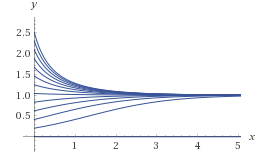
Fig. 2 Curve delle soluzioni dell’equazione logistica.
Ecco perché a Thanos, che ha pure la gemma del tempo, sarebbe bastato andare a sbirciare nel futuro per rendersi conto che tutti i suoi sforzi sono vanificati da questa semplice equazione! Purtroppo il nostro Titano, che non manca di ambizione e determinazione, difetta un po’ di pazienza…
Per i più curiosi, vediamo come si trovano esplicitamente tutte le soluzione dell’equazione logistica Per non complicarci la vita con troppi parametri, fissiamo \(\alpha-\omega=1\) e \(\sigma=1/4\). L’equazione da risolvere quindi è \[\left\{ \begin{array}{l}
\frac{dN}{dt}(t)=N(t)-\frac{1}{4}N^{2}(t)\\
N(0)=N_{0}.
\end{array}\right.\] In questo esempio il valore di equilibrio è \(4\).
Un’equazione del genere è detta a variabili separabili, e si risolve con un semplice trucco di integrazione. Dividiamo l’equazione per il secondo membro \[\frac{\frac{dN}{dt}(t)}{N(t)-\frac{1}{4}N^{2}(t)}=1\] e integriamo entrambi i membri tra l’istante iniziale \(0\) e un certo istante \(T\). \[\int_{0}^{T}\frac{\frac{dN}{dt}(t)}{N(t)-\frac{1}{4}N^{2}(t)}dt=\int_{0}^{T}1dt.\] Per il secondo membro abbiamo subito \[\int_{0}^{T}1dt=T,\] mentre per il primo membro usiamo la formula del cambio di variabile ottenendo \[\begin{aligned}
\int_{0}^{T}\frac{\frac{dN}{dt}(t)}{N(t)-\frac{1}{4}N^{2}(t)}dt & =\int_{N(0)}^{N(T)}\frac{1}{N-\frac{1}{4}N^{2}}dN=4\int_{N_{0}}^{N(T)}\frac{1}{N(4-N)}dN\\
& =\int_{N_{0}}^{N(T)}\frac{1}{N}-\frac{1}{4-N}dN=\ln\left|\frac{N(T)}{N_{0}}\right|-\ln\left|\frac{4-N(T)}{4-N_{0}}\right|,\end{aligned}\] quindi \[\ln\left|\frac{N(T)}{N_{0}}\frac{4-N_{0}}{4-N(T)}\right|=T\] che diventa \[\frac{N(T)}{N_{0}}\frac{4-N_{0}}{4-N(T)}=e^{T}\] e finalmente \[N(T)=\frac{4}{\left(\frac{4}{N_{0}}-1\right)e^{-T}+1}.\] Da questo si vede che \[\lim_{T\rightarrow+\infty}N(T)=4,\] che è proprio il valore di equilibrio. Inoltre la velocità di convergenza è di tipo esponenziale, quindi il tempo per arrivare al valore di soglia è rapido (sempre parlando in scale cosmiche).
Abbiamo scelto un modello molto semplice, altre scelte potevano essere fatte, magari sostituendo \(N^{2}\) con una diversa potenza. Questo però non avrebbe cambiato il tipo di soluzione, avrebbe solo reso il fenomeno della scarsità più evidente. Questo modello, quindi, seppur semplice, è robusto, ovvero il tipo di soluzione è lo stesso anche cambiando alcuni dei parametri in gioco.
Marco Ghimenti
Università di Pisa
Per approfondire
Marco Abate, Matematica e statistica. Le basi per le scienze della vita, McGraw-Hill Education, 2013.




















