Di fronte a un mondo in continua evoluzione, il concetto di ciclo di vita del prodotto emerge come una delle chiavi interpretative del successo e dell’obsolescenza dei beni. Questo approccio ha ispirato lo sviluppo di modelli matematici capaci di descrivere l’andamento delle vendite attraverso funzioni che riproducono le diverse fasi evolutive. In questo articolo di Corrado Binetti vediamo come si applicano questi concetti a dei prodotti alimentari — un formaggio artigianale, un olio d’oliva e un dolce tradizionale — in cui tradizione, sostenibilità e interventi di rilancio si integrano per rinnovare continuamente il percorso di vendita. 

Negli anni ’50 e ’60 del XX secolo, gli studiosi di marketing hanno iniziato ad analizzare il percorso che un prodotto compie dal momento del lancio fino al successivo declino, cercando così di individuare le fasi critiche e le opportunità d’intervento. È in questo contesto che Theodore Levitt, nel 1965, pubblicò il celebre articolo “Exploit the Product Life Cycle” sulla Harvard Business Review, ponendo le basi per una visione sistematica e strategica dell’intero processo. La teoria del ciclo di vita del prodotto ha profondamente influenzato la strategia aziendale, guidando non solo i processi di lancio ma anche la gestione di prodotti già consolidati sul mercato.

Il ciclo di vita di un prodotto: dalle funzioni cubiche ai modelli con rilancio

Come parte del percorso di Educazione Civica delle classi quinte, in linea con l’Obiettivo 11 dell’Agenda 2030: Città e comunità sostenibili, le classi VA Enogastronomia – Opzione prodotti dolciari e VE Enogastronomia dell’Istituto Alberghiero di Molfetta (BA) hanno unito competenze tecniche, scientifiche e gestionali per studiare il ciclo di vita di alcuni prodotti regionali, attraverso un’attività STEAM dal taglio laboratoriale e interdisciplinare. Grazie al supporto dell’intelligenza artificiale Copilot e ai contenuti teorici tratti dal compendio per docenti “Unità di apprendimento interdisciplinari – Triennio (DeA Scuola)”, allegato al volume “Colori della Matematica – Edizione Bianca, Volume A” di L. Sasso e I. Fragni, gli studenti hanno infatti analizzato il ciclo di vita di tre eccellenze gastronomiche pugliesi: la Burrata di Andria, l’Olio Extravergine di Oliva di Bitonto e il Sospiro di Bisceglie. 

A partire da dati statistici reali, raccolti e selezionati in autonomia, gli studenti hanno ricavato con l’aiuto di Copilot le curve di regressione per ciascun prodotto. L’osservazione dei grafici ha evidenziato come il modello di Levitt – modellizzato con una funzione polinomiale di terzo grado e già approfondito in un problema di realtà presente nel compendio — sia il più efficace nel descrivere l’andamento delle vendite.

Successivamente, generalizzando il nostro studio al ciclo di vita di un prodotto in ambienti diversi, in ottemperanza alle Linee guida per il passaggio al nuovo ordinamento degli Istituti professionali – Matematica – Secondo biennio e quinto anno (estratto dalla Direttiva n. 5 del 16 gennaio 2012): “Analisi e rappresentazione delle funzioni e dei loro grafici; interpretazione delle equazioni analitiche in contesti applicativi”, gli studenti hanno ricavato le formulazioni analitiche più rappresentative per ciascuno scenario. In particolare, hanno utilizzato:

• due diverse funzioni cubiche per rappresentare in modo accurato le fasi di sviluppo e maturità del prodotto, evidenziando la crescita fino al picco e il successivo declino in ambiente tradizionale ed ecosostenibile,
• una funzione razionale fratta per modellizzare con precisione il ciclo di vita in ambiente con rilancio, catturando le dinamiche di ripresa del mercato dopo il declino.

Infine, con GeoGebra hanno realizzato applet interattive dotate di slider, consentendo la variazione in tempo reale dei parametri funzionali e l’immediata interpretazione dei riflessi sulle curve di vendita.

Questo approccio ha permesso di coniugare rigore matematico, analisi statistica e contestualizzazione reale, offrendo agli studenti un’esperienza di apprendimento attiva, interdisciplinare e fortemente legata al territorio.

Ambiente Tradizionale

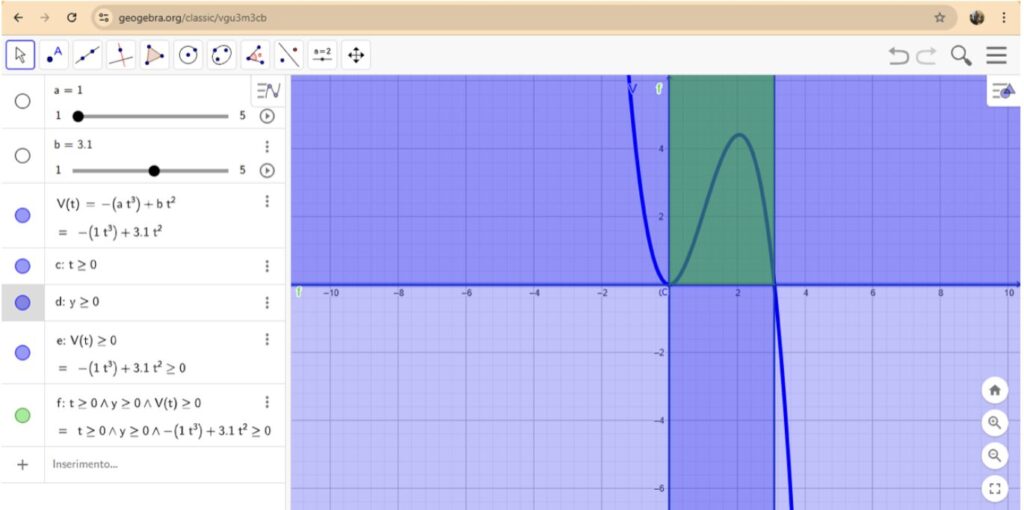
Il modello tradizionale riproduce il classico percorso di un prodotto: una crescita iniziale che porta a un picco nelle vendite, seguito da una fase di saturazione e infine da un declino. Nel contesto tradizionale, il ciclo di vita di un prodotto può essere modellizzato da una famiglia di funzioni cubiche della forma:
\(V(t)=−a t^3+b t^2\), dove \(a>0\) e \(b>0\).

• Passaggio per l’origine: Al tempo \(t=0\), non si registrano vendite, ovvero \(V(0) =0\).
• Concavità verso il basso: Il termine “\(-a t^3\)” garantisce che la funzione sia concava verso il basso, riflettendo la naturale transizione dalla fase di crescita a quella di declino.
• Vincoli pratici: L’analisi si focalizza sui valori \(t\geq 0\) e \(V(t) \geq 0\), esaminando solo il primo quadrante, dove le quantità di tempo e vendite assumono valori significativi e reali.

Guardalo su GeoGebra: https://www.geogebra.org/m/vgu3m3cb

Ambiente Ecosostenibile

Nel settore ecosostenibile, il modello viene adattato per riflettere l’impatto positivo delle pratiche ambientali avanzate. In questo caso, la famiglia di funzioni diventa:
\(Ve(t)=−a t^3+b t^2+ct\), dove sempre \(a>0\) e \(b>0\), \(c>0\) e in particolare \(c>b\).

Caratteristiche:

• Passaggio per l’origine: Poiché al lancio del prodotto non ci sono vendite, risulta \(Ve(0) =0\).
• Spinta ecosostenibile: Il termine \(ct\) apporta un rafforzamento iniziale alle vendite, evidenziando come un approccio green possa migliorare il trend di crescita.
• Mantenimento della concavità verso il basso: Pur aggiungendo il termine lineare, il termine “\(-a t^3\)” garantisce che, nelle fasi finali, la funzione rimanga concava verso il basso rappresentando il naturale declino post-picco.

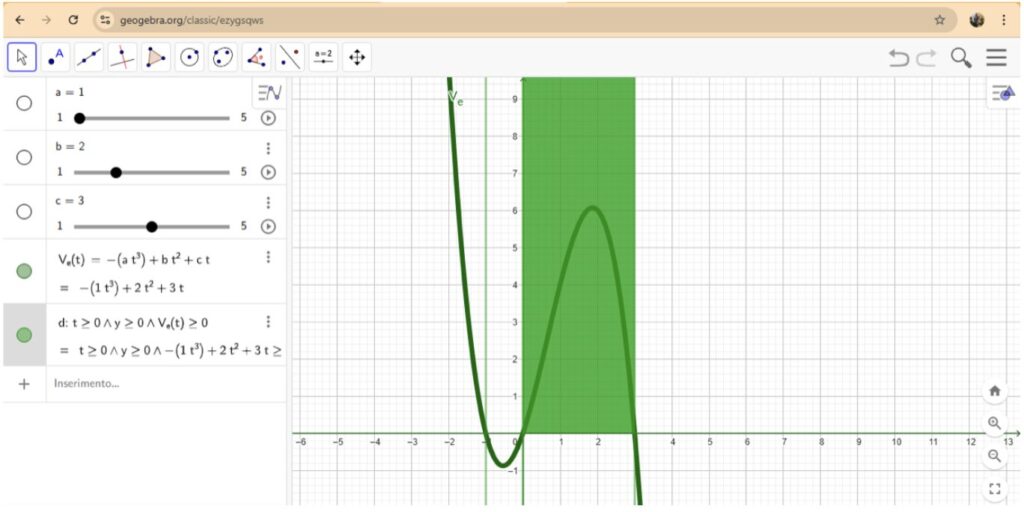
Guardalo su GeoGebra: https://www.geogebra.org/m/ezygsqws

Il confronto fra i due modelli appena studiati mette in luce come l’adozione di pratiche ecosostenibili possa favorire la crescita iniziale del prodotto, prolungando la fase di crescita prima che intervenga il declino.

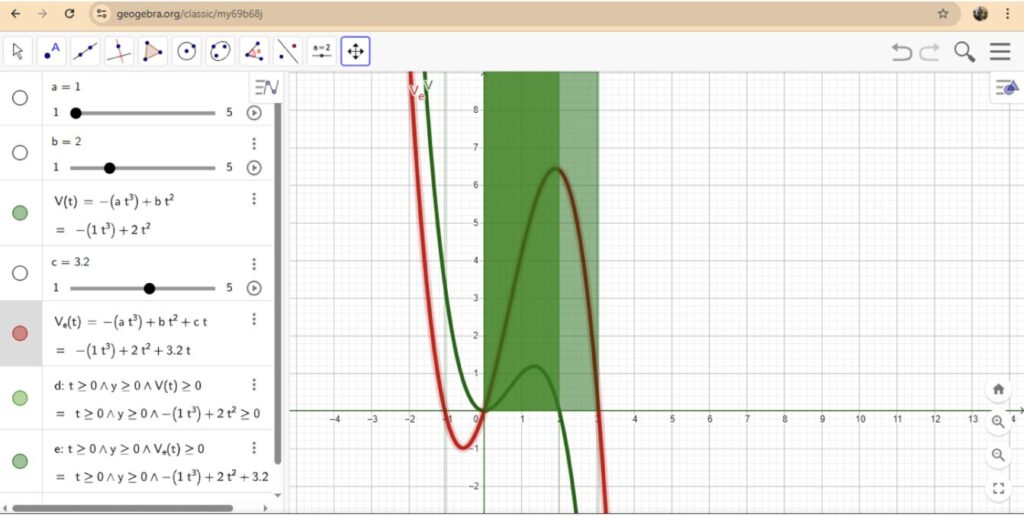
Guardalo su GeoGebra: https://www.geogebra.org/m/my69b68j

Introduzione della Fase di Rilancio

Per i prodotti di nicchia, che grazie a interventi mirati riescono a “rinvigorire” il ciclo di vita e a mantenersi competitivi per lunghi periodi, è utile modellare una fase di rilancio. In questo contesto, si è avuta la necessità di modellizzare la situazione con una funzione che presentasse le seguenti caratteristiche fondamentali:

• Passaggio per l’origine: la funzione deve soddisfare \(F(0) = 0\).
• Concavità verso il basso: l’andamento della funzione deve essere concavo verso il basso nell’intervallo di interesse, ossia quando \(t\geq 0\), per riflettere il naturale declino delle vendite dopo il picco, anche se parzialmente invertito dal rilancio.
• Asintoto orizzontale destro: la funzione deve tendere a un valore \(y=k\) con \(k>0\), rappresentando un plateau massimo di vendita in cui il prodotto, grazie al rilancio, si stabilizza nel tempo.

Una possibile formulazione che rispetta questi requisiti è data ad esempio dalla una famiglia di funzioni razionali fratte di terzo grado:
$$ F(t)= \frac{(k d t^3+b t^2+ct)}{(1+d t^3)}$$

Spiegazione delle componenti:

• Termine dominante e asintoto: Poiché per \(t\to\infty\) si ha \(\lim_{t\to\infty}F(t)= \lim_{t\to\infty}\frac{k d t^3}{d t^3}=k\)

il modello garantisce un asintoto orizzontale destro pari a \(y=k\), in cui \(k\) è un valore positivo (possibilmente abbastanza elevato), come richiesto.

• Passaggio per l’origine: l’assenza di termini costanti nel numeratore assicura che \(F(0)=0\).
• Concavità verso il basso: la scelta dei coefficienti \(b\) e \(c\) (eventualmente confrontata tramite lo studio della derivata seconda \(F′′(t)\) deve essere bilanciata in modo da mantenere la funzione concava verso il basso per \(t\geq 0\). Per ottenere questo aspetto, potrebbe essere utile fissare \(b\) vicino a zero o scegliere un \(c\) che garantisca che il termine negativo derivante dal comportamento della funzione domini nelle fasi finali.

Questa funzione fornisce un modello di rilancio in cui, dopo la fase di declino tipica del ciclo di vita, interventi strategici riescono a stabilizzare le vendite a un livello elevato e costante, rappresentato dall’asintoto \(y=k\).

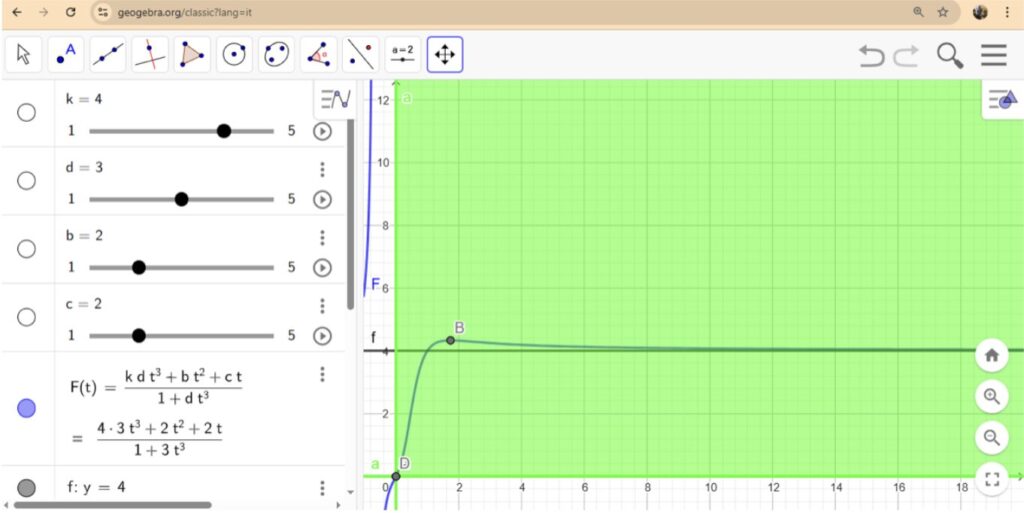
Guardalo su GeoGebra: https://www.geogebra.org/m/ftsjxdaj 

Nello studio dei tre contesti—ambiente tradizionale, ambiente ecosostenibile e fase di rilancio—con GeoGebra, lo slider ha permesso di variare in tempo reale i parametri \(a\), \(b\), \(c\), \(d\) e \(k\), evidenziando il legame tra ciascun coefficiente e la forma delle curve.

• In ambiente tradizionale le modifiche di \(a\) e \(b\), hanno evidenziato l’impatto su ampiezza e simmetria.
• In ambiente ecosostenibile la variazione di \(a\), \(b\) e \(c\) ha permesso di esplorare dinamiche di crescita e oscillazione in analogia con processi naturali.
• Nella fase di rilancio l’aggiustamento di \(b\), \(c\), \(d\) e \(k\) ha facilitato la simulazione di scenari di ripresa e potenziamento.

I vantaggi immediati per gli studenti derivanti dall’utilizzo di GeoGebra sono stati:

• Comprensione diretta del rapporto tra equazione analitica e grafico
• Sviluppo di pensiero critico nell’interpretazione dell’influenza di ogni parametro
• Rapidità nella sperimentazione “what-if” senza ricalcoli manuali
• Maggiore coinvolgimento grazie all’interattività e all’autonomia esplorativa

Questo approccio evidenzia come l’integrazione di strumenti digitali con un approccio scientifico trasformi l’analisi teorica in un’esperienza didattica dinamica e motivante.

Conclusioni e Spunti di Riflessione

L’attività svolta, nata dall’analisi del ciclo di vita di un prodotto e dalla lettura dei grafici presenti nelle fonti, ha rappresentato molto più di un esercizio tecnico: è stata un’esperienza di apprendimento autentico. Gli studenti, partendo da dati concreti, hanno saputo individuare – con il supporto del docente – le funzioni matematiche più adatte a descrivere le diverse fasi, passando dalla teoria alla pratica in modo naturale. Un’attività di questo tipo non è solo “fare matematica”: è allenare lo sguardo a leggere il mondo con strumenti rigorosi, ma anche creativi. Portare in classe un problema che nasce da un contesto reale – in questo caso il ciclo di vita di un prodotto – significa dare agli studenti la sensazione concreta che ciò che imparano non resti confinato nei libri, ma possa diventare chiave di lettura della realtà. Il cambiamento si è visto subito: più motivati, più curiosi, più pronti a mettersi in gioco. Non si sono limitati a seguire un procedimento, ma hanno proposto loro stessi le funzioni più adatte, guidati dall’interpretazione condivisa dei grafici. In quel momento la matematica è uscita dalla lavagna per diventare un linguaggio vivo, capace di raccontare storie e di fare previsioni. Questo approccio ha trasformato la lezione in un laboratorio di idee, dove la partecipazione non era un obbligo ma una conseguenza naturale dell’interesse. In quell’aula non stavamo solo tracciando curve su un grafico: stavamo imparando a leggere il mondo! 

L’integrazione di Copilot come supporto didattico ha aggiunto un ulteriore livello di efficacia metodologica: la sua capacità di reperire e sintetizzare istantaneamente dati statistici sul ciclo di vita di prodotto ha snellito le fasi di raccolta e validazione, consentendo agli studenti di concentrarsi sull’analisi qualitativa e sulla formulazione delle ipotesi. L’assistente AI ha facilitato la costruzione delle curve di regressione calibrando automaticamente i parametri iniziali e individuando anomalie nei dataset, migliorando la precisione del modello. Grazie al feedback contestuale e alle spiegazioni puntuali offerte in tempo reale, gli studenti hanno esercitato un apprendimento metacognitivo, valutando autonomamente la pertinenza delle scelte matematiche e sviluppando competenze digitali avanzate. Inoltre, l’utilizzo di GeoGebra affiancato all’AI ha permesso di arricchire l’esperienza con applet interattive dotate di slider, rendendo immediata la comprensione degli effetti della variazione parametrica e favorendo un approccio esplorativo-scientifico in grado di stimolare la creatività e l’autonomia di ciascun allievo nell’esplorare un contesto reale.

E quando la matematica diventa una lente per interpretare la realtà, ogni studente scopre di avere in mano uno strumento potente… e la voglia di usarlo.

Corrado Binetti

Monica Mattei