Continuiamo a parlare di gerrymandering, ovvero la pratica fraudolenta che consiste nel formare distretti elettorali in maniera partigiana, in compagnia di Nicola Apollonio.
Il 22 gennaio 2018, la Corte Suprema della Pennsylvania, accogliendo l’istanza di parte del League of Women Voters contro la distrettizzazione elettorale del 2011, adottata dalla legislatura repubblicana, in cui il parere di parte rintracciava una palese riduzione del bacino elettorale dei democratici, sentenziava “tale piano viola chiaramente la Costituzione della Pennsylvania e, su questa sola base, lo dichiariamo incostituzionale”. Perché la Matematica dovrebbe interessarsi ad una faccenda che ha tutta l’aria di una faccenda amministrativa, costituzionale, e politica? Beh, l’abbiamo spiegato qui su MaddMaths! in questo articolo: perché c’è di mezzo il gerrymandering, ovvero la pratica fraudolenta che consiste nel formare distretti elettorali in maniera partigiana. Come mostra il caso della Pennsylvania, in un sistema maggioritario uninominale, il gerrymandering è davvero in grado di influenzare significativamente l’esito delle elezioni ed è purtroppo sempre più difficile individuarlo. I gerrymanderer sono sempre più scaltri.
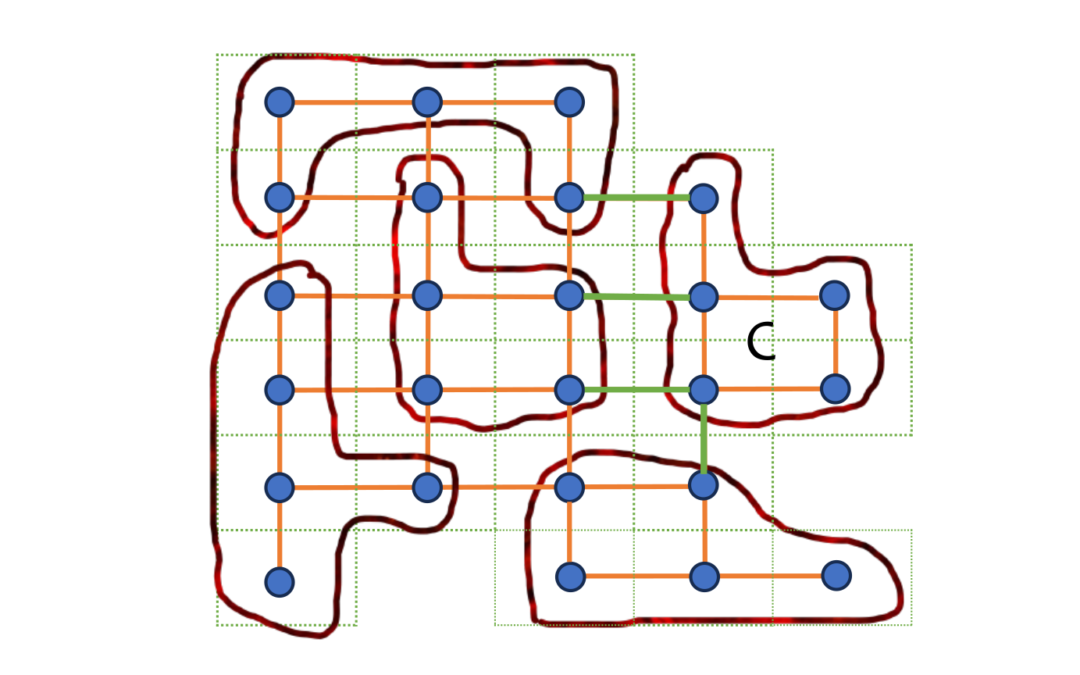
Omettendo per il momento qualche dettaglio, possiamo pensare ad una distrettizzazione elettorale in un territorio T, come una tassellazione di T, cioè una una suddivisione di T in porzioni contigue che chiamiamo distretti (figura (b)). I distretti sono a loro volta aggregazioni di porzioni elementari contigue che chiameremo unità (figura (a)). In Italia potremmo pensare le unità come i seggi elettorali, ossia i luoghi dove fisicamente ci si reca a votare. Le unità devono dunque essere interamente incluse o interamente escluse dai distretti (figura (b)).

Insomma abbiamo due partizioni di T, una in unità e l’altra in distretti e la distrettizzazione è una partizione meno fine della partizione in unità. Supponiamo che sul territorio T competano due partiti: il partito dei rossi ed il partito dei blu; ciascuno dei due partiti conosce la percentuale dei propri sostenitori in ciascuna delle unità (per esempio attraverso le serie storiche degli esiti delle elezioni). Se pensiamo i distretti come urne e le unità come palline il cui colore sia rosso o blu a seconda che in quell’unità abbia storicamente prevalso il rosso o il blu, allora il gerrymanderer rosso distribuirà le palline rosse di cui dispone in modo che sia massimo il numero di urne in cui è maggiore la proporzione di palline rosse.
Naturalmente quest’assegnazione di palline ad urne non può essere arbitraria perché
- i distretti devono essere porzioni connesse di territorio, deve essere cioè possibile raggiungere un’unità da una qualsiasi altra unità dello stesso distretto attraversando solo unità del distretto;
- i distretti devono avere un buon rapporto di forma; pertanto: a) l’indice di Polsby-Popper del distretto D, definito come il rapporto \(\frac{4\pi \text{Area(D)}}{\text{Perimetro(D)}^2}\) deve essere vicino ad 1; b) la distanza distD(u,v) tra due unità u e v del distretto D misurata nel distretto, pur non potendo essere più piccola della stessa distanza distT(u,v) tra le stesse unità misurata su tutto T (in T possono esistere scorciatoie che non esistono invece in D) non deve aumentare troppo; in altre parole la media dei rapporti deve risultare il più possibile vicina ad 1. Osserviamo che i due vincoli precedenti sono in grado di escludere distretti bizzarri come la salamandra che trovate qui, parzialmente eponima del termine gerrymandering;
- i distretti devono essere equi e, conseguentemente, la distrettizzazione perequata: i distretti devono avere grosso modo la stessa massa di elettori.
Ritornando dunque alla metafora delle urne, se la distribuzione di palline rosse deve essere ottenuta nel rispetto dei precedenti vincoli, come è possibile che essa si possa manipolare? In realtà non è poi così difficile costruire distrettizzazioni che soddisfino i vincoli geometrici imposti più sopra e che al tempo stesso favoriscano uno dei due partiti. L’avevamo suggerito nel nostro articolo del 2017 attraverso l’applicazione di un bel teorema di equipartizione. Il caso della Pennsylvania prova che non si tratta di un esempio di scuola. La geometria della distrettizzazione, a meno di manipolazioni marchiane, pur essendo severa, non lo è ancora abbastanza da prevenire il gerrymandering in ogni occasione.
Dobbiamo pensare a qualcos’altro. Qualcosa a cui in effetti siamo abituati a pensare: alla verosimiglianza di una data distrettizazione, cioè a quanto probabile sia l’osservarla nell’ipotesi che non vi sia manipolazione. Esattamente come la verosimiglianza di una data sequenza di testa e croci in un numero grande di lanci di una moneta che ipotizziamo non truccata: se osservassimo troppe più teste di quante attese certamente concluderemmo che la sequenza è almeno sospetta. Stiamo in effetti chiedendo aiuto alla probabilità e alla statistica, già tacitamente comparse nel cameo della metafora delle urne. A queste ultime dobbiamo però sottoporre il problema in una forma equivalente ma più digeribile, passando dalla geometria del piano alla geometria combinatoria, attraverso questo piccolo dizionario:

Il grafo G, illustrato in figura (c), è il geogràfo di T (T è visto come unione delle proprie unità). I geogràfi non sono grafi arbitrari; essi infatti godono dell’importante proprietà di essere planari, di poter essere disegnati cioè sul piano o sulla sfera senza che gli spigoli si intersechino se non nei vertici (una semplice osservazione che permette di enunciare e dimostrare il Teorema dei 4 Colori all’interno della Teoria dei Grafi). Questa costruzione, permette anche di tradurre il rapporto di forma di un distretto di T, misurato ad esempio con l’indice di Polsby-Popper, come il rapporto h(C)=(C)/|C|, dove |C| è il numero di vertici nella componente C, e (C) è il numero di spigoli che hanno un vertice in C e l’altro fuori di C. In figura (c), per il distretto etichettato con C, (C)è l’insieme degli spigoli verdi . Il rapporto h(C), che desideriamo mantenere piccolo, è legato al numero iso-perimetrico di G come l’indice di Polsby-Popper è legato alla disuguaglianza iso-perimetrica per D. Naturalmente, il dizionario qui sopra non elenca ancora i sinonimi di tutti i vincoli richiesti alle distrettizzazioni ma è già completo abbastanza per descrivere l’idea alla base di un metodo statistico-combinatorio per il riconoscimento del gerrymandering. Si tratta di studiare l’insieme (G,p) di tutte le equipartizioni C di un grafo G in p componenti connesse, soddisfacenti qualche richiesta sul valore di h(C) per ogni componente connessa C in C, in cui i vertici del grafo siano colorati di rosso e blu. Qui intendiamo equipartizione di G in senso lato come partizione il più possibile perequata. Non ci resta che formalizzare la verosimiglianza di un esito elettorale per una certa equipartizione C* di (G,p) (ovvero per una certa distrettizazione D*in (T,p)).
Presto fatto: abbiamo una fissata colorazione dei vertici del grafo in nodi rossi e blu (le unità in cui prevale il partito rosso o il partito blu); la colorazione delle unità induce poi una colorazione delle componenti (distretti) di C* in maniera naturale: una componente è rossa se contiene più vertici rossi che blu ed è blu altrimenti. Possiamo dunque agevolmente calcolare il numero r(C*) delle componenti rosse. La stessa cosa si può fare per ogni C in (G,p). Ora, al variare di C in (G,p), r(C) assumerà valori diversi ma determinati dalla corrispondente equipartizione C, sicché possiamo pensare l’esito elettorale come il valore osservato di una variabile aleatoria R ottenuto dopo aver estratto a caso una equipartizione dall’insieme—esattamente come osserviamo la sequenza di facce di una moneta dopo averla lanciata ripetutamente oppure la sequenza dei numeri estratti dal bussolotto di una tombola—. Infine, definiamo (C*) come l’insieme di tutte le equipartizioni C in (G,p) in cui r(C) è almeno pari ad r(C*). Questo insieme (che si chiama coda) contiene tutte le equipartizioni di G, che danno un esito per il partito rosso almeno tanto favorevole quanto quello dato da r(C*). Intuitivamente, più numerosa è la coda, tanto meno sospetto è il risultato osservato. Sicché ha senso definire la verosimiglianza dell’esito corrispondente a C* come il rapporto |(C*)|/|(G,p)| che altro non che la probabilità dell’evento (R ≥ r(C*)) assumendo una distribuzione di probabilità uniforme su (G,p). Tanto più bassa è tale probabilità, tanto più inverosimile è l’evento osservato.
Ma allora abbiamo lo strumento antifrode che volevamo? No! Purtroppo ancora no! Abbiamo solo trasferito tutta la difficoltà del problema nel calcolo della probabilità della coda e tale difficoltà è tutta combinatoria: non si conosce una formula per enumerare (G,p) e, d’altra parte, stiamo parlando di numeri enormi, per esempio nel caso in cui il grafo sia una griglia rettangolare anche solo 9 per 9, il numero delle distrettizzazioni con 9 distretti di 9 unità ciascuno è circa \(7\times 10^{14}\) .
Per avere un’idea di quello che succede, osserviamo che essendo G connesso, esso certamente contiene un albero ricoprente (un sottografo che abbia gli stessi vertici di G e che non contenga cicli); rimuovendo dall’albero p-1 spigoli, si ottengono p componenti connesse dell’albero; l’insieme dei vertici di ciascuna di tali componenti è l’insieme dei vertici di una componente connessa di G sicché ogni equipartizione di un albero ricoprente di G produce una equipartizione di G (sebbene alberi ricoprenti diversi possano produrre la stessa equipartizione di G). Per avere una formula basata su queste considerazioni, oltre a molti altri dettagli, dovremmo certamente essere capaci di 1) contare gli alberi ricoprenti (facile: Teorema di Kirchhoff anche noto come Matrix Tree Theorem[1 ]Il numero t(G) degli alberi ricoprenti di G è pari a 1/n volte il prodotto degli autovalori non nulli della matrice Laplaciana di G. L’ipotesi di connessione garantisce che la molteplicità dell’autovalore nullo sia zero sicché t(G) ha n-1 autovalori non nulli e t(G) si può calcolare efficientemente con i metodi dell’algebra lineare.) e 2) contare l’insieme degli alberi ricoprenti che generano una stessa equipartizione di G (difficilissimo). Se si aggiunge poi che il numero t(G) degli alberi ricoprenti di G, che si chiama a buon diritto, complessità di G, è dell’ordine[2 ]Si veda Grimmett GR, An upper bound for the number of spanning trees of a graph. Discrete Math. 16 (1976) 323–324 di \(n^{-1}(2m/(n-1))^{n-1}\) , dove m è il numero degli spigoli di G, si capisce bene, anche da questi conti alla buona, come sia difficile maneggiare (G,p). Dobbiamo purtroppo rinunciare al calcolo esatto e prendere un’altra strada: piuttosto che confrontare ciò che vediamo con ciò che ci aspetteremmo in assenza di manipolazioni, confrontiamo ciò che vediamo con un campione rappresentativo di ciò che ci aspetteremmo in assenza di manipolazioni. Questa è certamente la tendenza degli ultimi anni: piuttosto che trovare un modo per contare gli elementi di (G,p), ci “passeggiamo dentro”, abbastanza a lungo da poter capire come si comportano le equipartizioni virtuose e poterle poi confrontare con quelle eventualmente viziose.
Il metodo più utilizzato con cui esplorare (G,p) passeggiandovi dentro, è il metodo Markov-Chain MonteCarlo (MCMC)—Montecarlo si riferisce al Casinò e vi sono varianti Las Vegas—. L’idea generale è ancora semplice e possiamo descriverla impressionisticamente così: ci procuriamo una partizione virtuosa iniziale, ci procuriamo un metodo che, con alta probabilità, ci faccia passare da una equipartizione virtuosa ad un’altra (transizione) e, infine, cominciamo a passeggiare in (G,p) cominciando dall’equipartizione iniziale compiendo una transizione casuale ad ogni passo. Dopo un certo tempo (noto come mixing time) il metodo ci fornirà la proporzione delle equipartizioni virtuose, eventualmente raggruppate secondo certi criteri, contenute nell’urna delle equipartizioni di G. Abbiamo dunque il metodo antifrode? Non esattamente. Non sappiamo quanto a lungo dobbiamo passeggiare per ottenere questo risultato e passeggiare stanca (soprattutto costa)! Dovremo accontentarci di stime. Per il momento tuttavia, tali stime risultano abbastanza precise tanto da render questo approccio al riconoscimento del gerrymandering il più promettente tra quelli disponibili[3 ]Cory McCartan, Kosuke Imai, Sequential Monte Carlo for Sampling Balanced and Compact Redistricting Plans, https://arxiv.org/abs/2008.06131v5. Questi gerrymanderer!, Hanno tentato di ingannare la Geometria, ora tentano di ingannare il Caso. Se è vero che ne inventano sempre una nuova e anche vero che la Matematica ne inventerà sempre almeno una di più.
Nicola Apollonio
Note e riferimenti
| ⇧1 | Il numero t(G) degli alberi ricoprenti di G è pari a 1/n volte il prodotto degli autovalori non nulli della matrice Laplaciana di G. L’ipotesi di connessione garantisce che la molteplicità dell’autovalore nullo sia zero sicché t(G) ha n-1 autovalori non nulli e t(G) si può calcolare efficientemente con i metodi dell’algebra lineare. |
|---|---|
| ⇧2 | Si veda Grimmett GR, An upper bound for the number of spanning trees of a graph. Discrete Math. 16 (1976) 323–324 |
| ⇧3 | Cory McCartan, Kosuke Imai, Sequential Monte Carlo for Sampling Balanced and Compact Redistricting Plans, https://arxiv.org/abs/2008.06131v5 |