Nell’anno accademico 2015/16 presso l’Università di Roma Tre si è svolta la Scuola Astre. L’Alta Scuola Roma Tre (ASTRE) fa parte delle scuole superiori universitarie finanziate dal MIUR. Si tratta di una scuola biennale interdisciplinare: ASTRE riunisce studenti di tutti i corsi di laurea di Roma Tre, professori di Roma Tre e professori, italiani o stranieri, di chiara fama internazionale. Gli studenti, in numero di 40 per biennio, sono scelti, a seguito di domanda di ammissione e per selezione di merito, tra gli iscritti al primo anno dei corsi di laurea magistrale o al quarto dei corsi di laurea quinquennale. Gli studenti di ASTRE partecipano alle iniziative didattiche e scientifiche della Scuola. Ad essi è richiesto un impegno didattico supplementare in aula pari a circa cinquanta ore di lezioni per anno. Gli studenti ammessi alla Scuola ricevono una borsa di studio. Essi inoltre usufruiscono, nel corso del biennio, di diverse facilitazioni, nell’uso delle strutture di Roma Tre, che possano loro permettere un proficuo svolgimento degli studi supplementari a loro richiesti. All’interno di un corso di matematica la prova di esame consisteva nell’elaborazione di alcuni testi scritti a partire dal materiale proposto nel corso. I cinque migliori elaborati avevano la possibilità di essere pubblicati su MaddMaths!. Presentiamo il quinto e ultimo elaborato, di Marco Coccoli, del corso di Laurea in Economia e Management. Gli altri elaborati li trovate qui. 

«Comunque, dalla discussione venne fuori un’idea interessante. Uno di quelli che vi partecipava propose un gioco per dimostrare che gli abitanti del globo terrestre sono molto piu’ vicini l’uno all’altro, sotto molti punti di vista, di quanto lo siano stati nel passato. Dato un individuo qualunque tra il miliardo e mezzo di abitanti della terra, che vive in un posto qualsiasi, lui sosteneva di riuscire a mettersi in contatto con quell’individuo al massimo attraverso cinque altri individui che si conoscessero tra loro personalmente.» (da «Catene», racconto di Frigyes Karinthy)

Lo scrittore ungherese Frigyes Karinthy, nel racconto «Catene» ipotizza per primo quella che verrà poi definita come la teoria dei «Sei gradi di separazione», affermando che il mondo contemporaneo – pur avendo una popolazione maggiore rispetto al passato – è diventato più «piccolo» in quanto la possibilità di comunicare è aumentata e le relazioni possono essere implementate in maniera molto più semplice e veloce. Così, mentre per Giulio Cesare sarebbe stato praticamente impossibile mettersi in contatto con uno sciamano azteca, nel ventesimo secolo una qualsiasi persona – è questo l’assunto della teoria – può essere collegata ad un’altra persona attraverso una catena di conoscenze che prevede non più di sei passaggi.   

La teoria, semplice e affascinante, ebbe però un primo riscontro scientifico solamente nel 1967, grazie alla sperimentazione del sociologo statunitense Stanley Milgram che si ispirò  alla lettura del romanzo di Karinthy. Milgram, docente di Psicologia sociale ad Harvard, seleziona un campione casuale di abitanti del Midwest e chiede loro di inviare un plico ad una persona «target» del Massachussets senza specificarne l’indirizzo, ma solo l’occupazione e la zona generica di residenza.

Ogni persona avrebbe dovuto tentare di recapitare il plico al destinatario finale utilizzando una catena di conoscenti che, nella loro opinione, avessero una qualche possibilità di conoscere il destinatario. (A conosce B che conosce C che conosce D……. che conosce il Target finale). Le regole del gioco erano abbastanza semplici: “1. Add your name to the roster at the bottom of this sheet, so that the next person who receives this letter will know who it came from. 2. Detach one postcard. Fill it out and return it to Harvard University. No stamp is needed. The postcard is very important. It allows us to keep track of the progress of the folder as it moves toward the target person. 3. If you know the target person on a personal basis, mail this folder directly to him. Do this only if you have previously met the target person and know each other on a first name basis. 4. If you do not know the target person on a personal basis, do not try to contact him directly. Instead, mail this folder to a personal acquaintance who is more likely than you to know the target person. You may send the folder to a friend, relative or acquaintance, but it must be someone you know on a first name basis.”

Milgram e i suoi collaboratori di Harvard pensavano che la catena avrebbe comportato almeno un centinaio di passaggi prima di arrivare al destinatario. Invece, sorprendentemente, il numero medio dei passaggi registrato fu tra i cinque e i sette passaggi. L’aspetto importante dell’esperimento è che gli attori erano tutti di estrazione diversa, a dimostrazione del fatto che il «mondo piccolo» non era composto da un campione omogeneo e che la teoria dei «sei gradi» era valida indipendentemente dalle classi e dagli ambienti.  In verità le conclusioni a cui giunse Milgram non avevano poi basi così solide dal punto di vista scientifico, anche in considerazione del fatto che la media dei «sei passaggi» fu calcolata solo sulla piccola parte delle lettere arrivate a destinazione (circa il 5%) e che la maggior parte delle “catene” non si concluse positivamente. Ma, nonostante questo, il suo esperimento ebbe una eco mondiale e ispirò moltissime opere teatrali, letterarie e cinematografiche finendo poi per essere definito da tutti come la base della teoria dei «sei gradi di separazione».

Solo con l’avvento di Internet però fu possibile validare la teoria sulla base di dati davvero reali. Fu Duncan Watts, professore della Columbia University che simulò nel 2001 l’esperimento di Milgram utilizzando le e-mail al posto delle lettere. Su un campione di 48.000 persone distribuite in tutti i paesi del mondo, la media dei passaggi prima di arrivare al target fu effettivamente di circa sei.  

Un’altra prova sul Web fu fatta tramite gli utenti di «Messenger» e il risultato, anche in questo caso, fu di poco superiore ai sei gradi (6,6). L’ipotesi quindi – anche se non suffragata da formule matematiche – inizia a diventare una “quasi certezza”, riassunta molto bene dallo scienziato ungherese Albert-László Barabási: «Sulle strade affollate di qualsiasi metropoli solo pochi gradi separano due individui dati; e solo pochi gradi separano tutti noi. Anzi stupisce quanto raramente notiamo la struttura di piccolo mondo e quanto spesso crediamo che il nostro mondo prossimo ci sia molto lontano. Non è una coincidenza nemmeno che le connessioni del cervello umano presentino la stessa architettura di piccolo mondo delle reti sociali, né che ritroviamo il medesimo modello del Web, nella struttura del linguaggio o nelle catene alimentari. Se fosse una coincidenza, sarebbe una coincidenza davvero incredibile.»

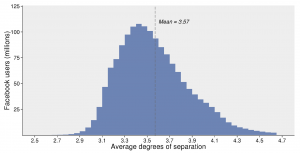Ma un’altra prova significativa della credibilità della teoria dei sei gradi di separazione arriva con il diffondersi dei social network. Grazie all’alto numero di utenti registrati su Facebook (circa 1,6 miliardi) è stato possibile effettuare una sperimentazione su presupposti scientifici molti più validi rispetto a quella di Milgram. Il risultato stupisce ancora una volta: «Ogni persona nel mondo (ovviamente del mondo degli utenti di Facebook) è collegata a qualsiasi altra persona tramite un numero medio di intermediari pari a 3,57». Questo è il risultato a cui giungono non solo i ricercatori di Facebook, ma anche altri ricercatori indipendenti.

Una teoria affascinante che può essere vista sotto diversi punti di vista a partire da quello più strettamente matematico:

È una formula a regolare le relazioni nel mondo: Il fascino di una teoria matematica.

Il fascino dei «sei gradi» non poteva lasciare indifferenti i matematici che tentarono da subito di individuare una formula in grado di dare una dimostrazione della teoria partendo dal postulato: «Dato un insieme di N persone, qual è la probabilità che ogni membro di N sia connesso a un altro membro attraverso $$k_1$$, $$ k_2$$, $$k_3$$…$$k_n$$ collegamenti?»

Negli anni cinquanta, prima ancora dell’esperimento di Milgram, i due matematici Ithiel de Sola Pool del MIT e Manfred Kochen della IBM, tentarono senza successo di dare una risposta.

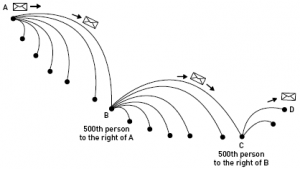L’approccio matematico parte da un assunto di un mondo «ordinato» e non «casuale». L’immagine evocata è quella della popolazione mondiale (stimata all’epoca in 6 miliardi) disposta a cerchio (anello reticolare) e con l’ipotesi che ogni persona abbia una media di mille «conoscenti» disposti la metà a destra e un’altra metà a sinistra. Per simulare l’esperimento Milgram in questo «mondo ordinato» si seleziona una persona nel cerchio e si chiede di inviare «la lettera» alla persona situata direttamente di fronte per il tramite del suo ultimo conoscente (il cinquecentesimo) situato alla sua destra.

A sua volta questo la consegnerà al suo ultimo conoscente situato alla sua destra. Viaggiando in questo modo (cioè a blocchi di 500) ci si chiede quante connessioni saranno necessarie per recapitare la lettera. Considerando che il destinatario è di circa 3 miliardi di persone lontano dal mittente, la lettera attraversa 500 persone per connessione, si comprende che questo mondo «ordinato» e matematico ha molti più «gradi di separazione» rispetto al mondo casuale di Milgram.

Considerando che distanza media, d, tra nodi su un grafico casuale è dato dalla formula:

$$d=1+\frac{\ln{N}}{\ln{k}+\ln{(k-1)}}$$

dove N = numero di nodi, k = numero di link per nodo.

Sostituendo i nostri valori per N= 6 miliardi e k = 1.000 avremo:

$$d=1+\frac{\ln{6\times10^9}}{\ln{10^3}+\ln{(10^3-1)}}$$

che significa circa 2,6 connessioni a persona. Ciò implica che, in un mondo «non ordinato» ci vorrebbero quasi tre connessioni in media per passare una lettera da una persona ad un’altra. Questo potrebbe dimostrare che il mondo sperimentato di Milgram non può essere un mondo «ordinato», ma solo «casuale».

Il punto di vista socio-culturale: Solo 5 persone tra me e il Presidente Obama, solo due tra Alvaro Vitali e Robert De Niro.

Questo concetto di «piccolo mondo» e della stretta interconnessione tra le persone ha sempre ispirato la fantasia umana. E’ sicuramente suggestiva l’idea che – tramite una rete di soli cinque (o forse meno) conoscenti – qualsiasi individuo del pianeta possa arrivare ad Obama o a qualsiasi altra celebrità della terra. Il concetto sembrerebbe più facilmente comprensibile se queste relazioni fossero confinate in un medesimo ambiente socio-culturale o geografico, un campione omogeneo, ma in realtà non è così. O meglio: se ripetiamo l’esperimento di Milgram in un ambiente più ristretto, i risultati sono ancora più sorprendenti.

Il sito «The Oracle of Bacon» effettua il test dei «sei gradi» su un ambiente apparentemente più ristretto: la popolazione mondiale di tutti gli attori cinematografici. Il concetto di «conoscenza» o di «punto di connessione» è quello di aver fatto un film insieme, concetto che, effettivamente, sottende almeno il fatto di essersi incontrati sul set cinematografico. Ebbene, i passaggi richiesti tra qualsiasi attore di   genere e di qualsiasi nazionalità sono tra due e tre.

La teoria in questione, ispirata da un racconto, ha inoltre ispirato a sua volta un buon numero di opere artistiche. La stessa espressione di «sei gradi di separazione» non fu affatto introdotta da Milgram, ma da una commedia teatrale di John Guare e dall’omonimo film del 1993.

Una delle protagoniste del film meditando sull’interconnessione delle persone afferma: «Sei gradi di separazione fra noi e tutti gli altri su questo pianeta: un aborigeno australiano, uno della Terra del Fuoco, un eschimese. Ognuno di noi è una porta spalancata su altri mondi.»

Molte altre opere cinematografiche riprendono il tema centrale dei sei gradi di separazione. «Magnolia» (1999) di Paul Anderson racconta nove storie apparentemente separate e invece straordinariamente connesse, mentre «Crash» (2004) di Paul Haggis mostra un ambiente unico (la città di Los Angeles) in cui classi di persone appartenenti a universi diversi sembrano non incontrarsi mai se non per uno «scontro» che rivelerà però la «connessione entro i sei gradi» anche tra individui completamente diversi tra loro per classe, ceto, etnia, religione.

Solo sei gradi: ma per fare cosa? Il rischio «aborigeno».

La possibilità di essere rapidamente interconnesso con qualsiasi persona al mondo è sicuramente affascinante dal punto di vista «matematico» e «sociale», ma, al di là delle suggestioni ci si dovrebbe chiedere a cosa e a chi davvero possa servire.

Altrimenti si rischia di confinare il tutto in una formula matematica e la possibilità di entrare rapidamente in contatto con persone diametralmente diverse per condizione, geografia, etnia, occupazione rischia di portarci alla fatidica domanda posta dal comico Corrado Guzzanti nel suo celebre monologo sulla rete e l’aborigeno.

In effetti il modello matematico delle reti di contatti ha avuto alcune applicazioni nel campo della medicina (diffusione delle malattie infettive) e delle telecomunicazioni, ma indubbiamente l’utilizzo più efficace può essere quello nel mondo del social marketing e dei social network in generale, con tutte le implicazioni commerciali che questi ambienti implicano. Non è un caso che uno dei primi social network, lanciato forse troppo presto nel 1997, si chiamasse proprio «SixDegrees.com» ed era basato sulla possibilità di verificare «gli amici degli amici» fino al sesto grado.

Non è un caso anche che proprio Facebook e Yahoo abbiano promosso iniziative ed esperimenti basati sulla teoria dei «sei gradi» per testare come un messaggio qualsiasi possa diffondersi in maniera «virale» sulla rete. E’ notizia recente lo sviluppo di una App che veicola messaggi pubblicitari su una rete di «amici» all’interno dei social network in cambio di un piccolo compenso a favore del’utente «veicolo».

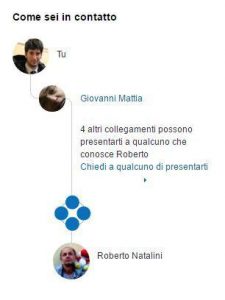
Ma il social network che può capitalizzare di più sulla teoria dei «sei gradi» è senza dubbio «Linkedin». E infatti questo «social» dedicato al mondo del lavoro ha recentemente sviluppato, con grande soddisfazione degli utenti, la funzione «How you’re connected», in cui ogni utente può vedere quanti «gradi» lo separano da un manager di una azienda target, o da chiunque possa essere utile contattare per il proprio lavoro, visualizzando graficamente la rete delle proprie conoscenze che lo potrebbero portare alla conoscenza della persona stessa.

Marco Coccoli