In quanti modi posso fare ambo al gioco del Lotto? In quanti modi possono ricadere due dadi lanciati in aria? Quante sono le possibili schedine del totocalcio? Quante strette di mano ci saranno tra cinque amici che s’incontrano? Sono domande a cui risponde il Calcolo Combinatorio. Conoscere le risposte ci aiuta a saper scegliere in modo consapevole e, soprattutto, a non rovinarci al gioco! Anna Cerasoli, matematica, insegnante, scrittrice, divulgatrice, ci propone una piccola introduzione in tre puntate, una volta la settimana, a questa parte della matematica, così semplice e spesso divertente, che però trova poco spazio nei programmi didattici. Tutte le puntate le ritrovate raccolte in questa pagina.

Eccoci di nuovo a fare un po’ di conti, conti facili e soprattutto interessanti perché rispondono a domande che possono sorgere da semplici problemi quotidiani. In questa seconda parte incontrerete altri due facili modelli:

Quadri alla parete
Alcuni quadri alla parete

Chi non si è trovato a decidere come sistemare dei quadri lungo una parete? Ecco un facile esempio in cui i magnifici Charlie Brown, Snoopy e Linus, sono pronti a fare bella mostra, uno dopo l’altro, su una parete.

In quanti modi diversi possiamo appenderli ai tre chiodi? Il solito diagramma ad albero ci risolve il problema.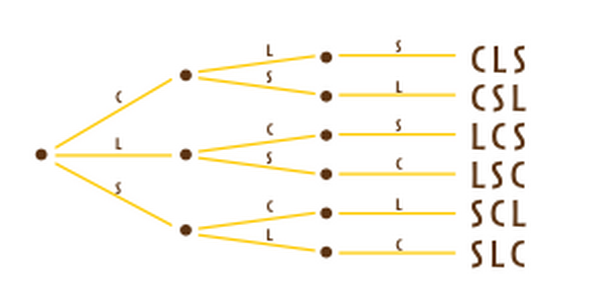Un albero particolare perché inizia con 3 rami, da ciascuno dei quali partono altri 2 rami, che a loro volta terminano con 1 solo ramo. Quindi

3x2x1= 6

rami finali che indicano i 6 diversi modi di ordinare i quadri. E se i quadri fossero 4? E’ facile immaginare che in questo caso l’albero avrebbe 4 rami iniziali, da ciascuno dei quali ne partirebbero 3, poi 2, poi 1, dunque:

4x3x2x1=24

diversi modi. Lo stesso ragionamento ci porta a dire che se i quadri fossero 5 avremmo

5x4x3x2x1=120

diversi modi di appenderli in fila. È sorprendente pensare che bastano 2 quadri in più perché i modi di appenderli in fila passino da 6 a ben 120. Ed è proprio questa sorpresa che ha determinato il simbolismo (n seguito da un punto esclamativo) con cui si rappresenta questa speciale operazione, che indica tutte le permutazioni di n oggetti. Il loro numero è dato dal prodotto tra n e tutti i numeri naturali che lo precedono.

n! = n (n-1) (n-2)… (2)(1)

Simbolo che troviamo anche su un tasto della nostra calcolatrice, e che si legge enne fattoriale, per dire che è il prodotto di n fattori. D’ora in poi, tutti i problemi in cui si tratterà di ordinare n oggetti, potranno essere riferiti al modello quadri alla parete. Per esempio: in quanti modi possono salire sul podio i 3 vincitori di una corsa?

Sullo stesso modello ecco un altro esempio che stupirà anche i più cinici: consideriamo la sequenza del nostro alfabeto

ABCDEFGHILMNOPQRSTUVZ

Questa è una sua permutazione

    BACDEFGHILMNOPQRSTUVZ

Ebbene, se volessimo cambiare di posto, in tutti i modi possibile, le 21 lettere avremmo ben

\(\Large 21! = 51.090.942.171.709.440.000\)

diverse permutazioni. E se una stampante ne scrivesse 100 al secondo (pari a 2100 caratteri al secondo, cioè 126.000 al minuto) stamperà \(100\times60\times60\times24\times365 = 3.153.600.000\) stringhe ogni anno.

21! : 3.153.600.000= 16.200.831.485 di anni, perciò più di 16 miliardi di anni.

Veniamo al prossimo modello: alcuni quadri alla parete. Supponiamo di avere più quadri, per esempio 5, tra cui scegliere i 3 da appendere ai nostri 3 chiodi: Charlie Brown, Snoopy, Linus, Woodstok e Pig Pen

Usiamo di nuovo un albero matematico: avrà 5 rami iniziali per scegliere il primo quadro, 4 rami per scegliere il secondo, e infine 3 rami per il terzo quadro.

Dunque avremo

\(\Large 5\times4\times3 = 60\)

diversi modi di appendere 3 quadri scelti tra 5. Questa speciale operazione viene indicata con il simbolo

\(\Large (5)_3\)

Parlando in generale: il numero n tra cui scegliere è tra parentesi e il numero di oggetti da scegliere è scritto più piccolo, in basso a destra k.

\(\Large (n)_k\)

Si legge “n con k”. I matematici chiamano disposizione ciascuna di queste sequenze. Per noi sarà il modello alcuni quadri alla parete a guidarci nella risoluzione di problemi ad esso riferibili.E per restare in tema di gare calcoliamo tutti i modi in cui 20 partecipanti ad una corsa possono presentarsi sul podio. Sono

\(\Large 20 \times 19 \times 18= 6840\)

Infine, ecco pronto un semplice esercizio: con 4 colori

quante diverse bandierine si possono disegnare? Queste sono solo alcune, completa l’elenco.

Buon lavoro! Alla prossima puntata!        

2-continua

Anna Cerasoli

Tutte le puntate le ritrovate raccolte in questa pagina.     

BIBLIOGRAFIA

• Anna Cerasoli. Sono il numero 1. Come mi sono divertito a diventare bravo in matematica!  con Ilaria Faccioli (Illustratrice), Feltrinelli, 2008, Collana: Feltrinelli Kids,129 p., ill. , Brossura, EAN:  9788807921278.

• Anna Cerasoli. La sorpresa dei numeri. Un viaggio nella matematica simpatica,  con A. Gon (Illustratore), Editoriale Scienza, 2013, Collana: Non solo numeri. Pagine: 176 p., ill. , Rilegato, EAN: 9788873076209.

• Anna Cerasoli. Matematica amica. Ediz. illustrata, con Gaia Stella (Illustratrice), Feltrinelli, 2016. Collana: Feltrinelli Kids. Saggistica narrata. 124 p., ill. , Brossura. Età di lettura: Da 8 anni. EAN: 9788807922787

Crediti delle immagini. Se non indicato le immagini sono di proprietà dell’autrice.