Una nuova mini-serie, fatta di video e articoli, di Alessandro Zaccagnini, matematico, esperto di teoria dei numeri, autore della fortunata serie “Dialogo sui numeri primi“, questa volta per raccontarci tante diverse dimostrazioni di un unico Teorema.

Teorema (Euclide). Esistono infiniti numeri primi.

Ho trovato almeno una dozzina di diverse dimostrazioni di matematici piú o meno famosi: Euclide, Eulero (almeno due, forse tre), Erdős, Goldbach, Schur, Fürstenberg, Washington, …, solo per citarne alcuni. Di queste ne ho scelte sette, che illustrerò nelle varie puntate. Dimostrare lo stesso teorema tante volte è un po’ come far dipingere lo stesso quadro a piú artisti diversi, ciascuno dei quali sceglie la propria prospettiva e tecnica, illustrando un aspetto diverso dagli altri. Ho provato a immaginare la mappa concettuale delle idee che sono state usate per le dimostrazioni di cui parlerò: al centro ci sono i numeri primi, e tutto intorno oltre all’aritmetica troviamo algebra, combinatoria, analisi matematica reale e complessa …

A me interessa sempre mostrare la matematica come una sola cosa, unitaria, perché penso che le classificazioni disciplinari rigide siano arbitrarie e in definitiva facciano un torto alla matematica stessa. Quando un matematico vuole dimostrare un teorema, prende o talvolta crea gli strumenti di cui ha bisogno senza curarsi troppo della loro classificazione. Tra i miei obiettivi c’è, appunto, mettere in connessione varie idee matematiche anche, apparentemente, distanti fra loro.

Nel fare le ricerche per questa serie ho tratto spunti principalmente da tre fonti, e cioè i libri di Aigner & Ziegler, “Proofs from the Book,” di Ribenboim, “The Book of Prime Number Records” e anche la rispettiva pagina di Wikipedia. Si tratta in ogni caso di rielaborazioni personali. L’ordine con cui illustrerò le dimostrazioni è arbitrario, tranne per il fatto che il primo posto spetta di diritto ad Euclide. Le sette dimostrazioni che ho scelto sono “elementari,” cioè usano per la maggior parte matematica di base: in qualche caso mi limiterò ad illustrare la dimostrazione per mezzo di esempi, riportando i dettagli nei documenti scritti che accompagnano i video.

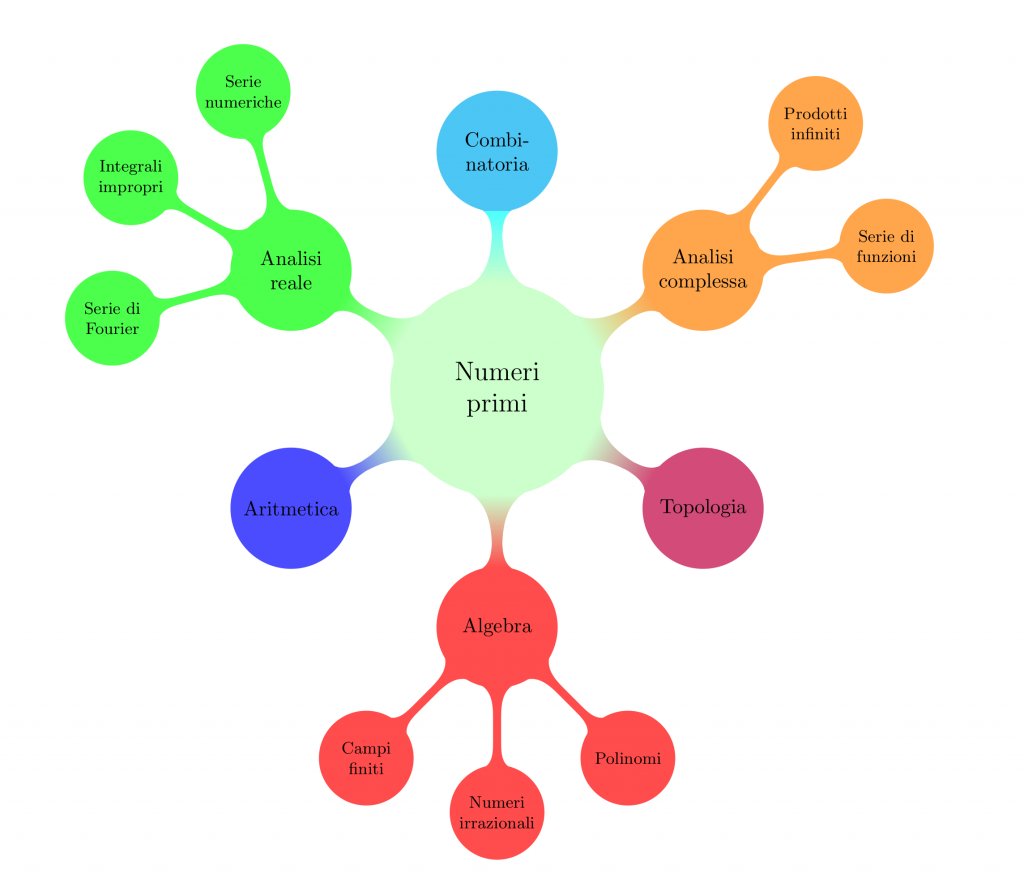
A conclusione di questa presentazione, voglio accennare ad un paio di principi ricorrenti nelle dimostrazioni. In molti casi conteremo i numeri interi che hanno determinate caratteristiche, tipicamente vincoli nella loro scomposizione in fattori primi: questo ci permetterà di ottenere informazioni qualitative o quantitative che implicano il Teorema di Euclide. Un altro principio importante, in effetti il cardine di tutte le nostre dimostrazioni, è Teorema fondamentale dell’aritmetica, il quale implica che la moltiplicazione è un’operazione “rigida.” Vedremo questo concetto in azione molte volte nel corso delle dimostrazioni che ho selezionato.

Buon divertimento!

Alessandro Zaccagnini