Alessia Cattabriga e Michele Mulazzani, docenti di geometria dell’Università degli Studi di Bologna, commentano per MaddMaths! l’articolo di Quanta Magazine sulla scoperta di Lisa Piccirillo a proposito del Nodo di Conway.
Prendiamo una corda, annodiamola a piacimento e incolliamo tra loro gli estremi liberi: l’oggetto che abbiamo ottenuto è chiamato dai matematici nodo. Il video mostra come costruire il nodo “annodato” più semplice, chiamato nodo trifoglio. Non è però il più semplice in assoluto, dato che anche quello che si ottiene chiudendo una corda senza annodarla è considerato un nodo ed è chiamato nodo banale.
Ovviamente i nodi matematici sono oggetti ideali, in quanto, a differenza della corda reale, sono curve lisce, cioè prive di spessore e in grado di allungarsi o accorciarsi a piacimento. Questi oggetti apparentemente così semplici, sono essenziali per lo studio degli oggetti (varietà) a 3 e 4 dimensioni, e trovano importanti applicazioni nella fisica teorica e nei modelli biochimici.
Tornando alla nostra corda iniziale, una volta chiusa la corda è possibile manipolarla cambiandone la forma, ma non la sostanza di annodamento: allo stesso modo due nodi sono considerati uguali se è possibile deformare uno nell’altro senza che la curva si auto-attraversi durante la deformazione; ad esempio, non è troppo difficile convincersi con l’ausilio di una corda che anche il nodo in Figura 1 è un nodo trifoglio, anche se in generale non è per nulla semplice capire se due nodi sono uguali o meno.

Figura 1: nodo trifoglio
E’ proprio un particolare nodo, quello riportato in Figura 2 che, nell’estate del 2018 durante una conferenza, ha attirato l’attenzione della giovane matematica Lisa Piccirillo, all’epoca dottoranda dell’Università del Texas.

Figura 2: nodo di Conway
Il nodo che ha affascinato Lisa, porta un nome importate, quello del famoso matematico John Horton Conway, deceduto l’11 aprile di quest’anno all’età di 82 anni a causa di complicanze legate al COVID-19. La storia di questo nodo è avvincente: infatti è dal 1970 che il nodo di Conway riceve le attenzioni di numerosi matematici interessati a capire se sia o meno un nodo “slice”, mistero definitivamente svelato da Lisa, cosa che le la fruttato una pubblicazione su Annals of Mathematics, probabilmente la rivista internazionale più prestigiosa in ambito matematico. Ma cosa vuol dire per un nodo essere slice? Partiamo osservando, che il nodo banale altro non è che una circonferenza e quindi ha la proprietà di essere il bordo di un cerchio; un’osservazione assai meno banale, è che questo nodo è l’unico ad avere tale proprietà: se provassimo ad incollare un cerchio lungo un qualsiasi altro nodo, avendo la libertà di piegarlo e stirarlo, come se fosse di pongo, ma non di farlo auto-attraversare non ci riusciremmo mai. Se però invece di muoverci nello spazio tridimensionale, aggiungessimo una quarta dimensione, la nostra libertà di movimento crescerebbe e a volte potremmo riuscirci. Per capire come, pensiamo ad un incrocio stradale: esso sta su un piano, ma, uscendo dal piano e costruendo un ponte possiamo evitarlo. Allo stesso modo, usando una quarta dimensione è possibile rimuovere gli auto attraversamenti del disco in Figura 3.

Figura 3: ribbon knot
Ecco quindi cos’è un nodo slice: è un nodo che è il bordo di un cerchio che vive nello spazio a 4-dimensioni.
Non tutti i nodi sono slice, ad esempio il trifoglio non lo è, e in generale, seppur molto importante per lo studio degli oggetti 3 e 4 dimensionali, non è facile capire se un nodo sia slice o meno. Particolarmente difficile era il caso del nodo di Conway: infatti, se da un lato non sembrava avere le carte in regola per essere slice, dall’altro si sapeva essere un parente molto stretto di un nodo slice, il nodo di Kinoshita-Terasaka, a cui è legato da una cosiddetta mutazione (vedi Figura 4).
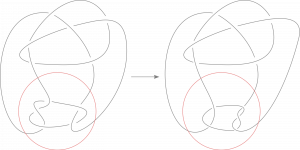
Figura 4: mutazione
Questa situazione rendeva il nodo di Conway resistente alle tecniche generalmente utilizzate per dimostrare che un nodo non è slice.
Lisa Piccirillo è stata la persona giusta al momento giusto: facendo uso di costruzioni 4-dimensionali che stava analizzando e sviluppando nel suo dottorato, Lisa è riuscita ad aggirare il problema: invece di lavorare direttamente sul nodo di Conway, ha costruito un altro nodo con la proprietà che o entrambi i nodi erano slice o nessuno dei due lo era. Il nuovo nodo era apparentemente più complesso, ma non sembrava avere parentele con altri nodi slice: questo ha permesso a Lisa di usare con successo una tecnica già nota per dimostrare che in effetti non era slice, risolvendo così, in pochi giorni e con un elegante dimostrazione, una congettura aperta da decenni.
Questo risultato insieme agli altri ottenuti durante il suo dottorato hanno assicurato a Lisa una posizione post-doc presso il prestigioso MIT, Massachusetts Institute of Technology.
Curiosità: la traduzione italiana del termine slice è fetta: la ragione è che, come il nodo banale si ottiene affettando una superficie sferica nello spazio 3D, così un nodo slice si può ottenere affettando una superficie sferica annodata che vive nello spazio a quattro dimensioni!
La foto di copertina è di Lisa Piccirillo ed è stata presa dalla sua pagina web.













