Marco Menale intervista Angelo Vulpiani per parlare del libro “A Random Walk in Physics”, scritto assieme a Massimo Cencini, Andrea Puglisi e Davide Vergni.
 Angelo Vulpiani è professore di Fisica Teorica presso l’Università degli Studi di Roma “La Sapienza”. I suoi interessi di ricerca riguardano caos, turbolenza e meccanica statistica. A lui si aggiungono altri tre autori, prima suoi tesisti e dottorandi, e ora collaboratori. Massimo Cencini e Andrea Puglisi sono ricercatori dell’Istituto dei sistemi complessi del CNR. Cencini si occupa principalmente di turbolenza e fluidodinamica, mentre Puglisi di meccanica statistica di non equilibrio. Il quarto autore è Davide Vergni dell’Istituto per le Applicazioni del Calcolo “Mauro Picone” del CNR. Si occupa di matematica applicata, dai modelli finanziari (modelli di gestione del debito pubblico, in collaborazione con il Ministero del Tesoro) ai sistemi biologici (analisi dei network biologici con applicazioni mediche, in collaborazione con diversi centri di ricerca ospedalieri).
Angelo Vulpiani è professore di Fisica Teorica presso l’Università degli Studi di Roma “La Sapienza”. I suoi interessi di ricerca riguardano caos, turbolenza e meccanica statistica. A lui si aggiungono altri tre autori, prima suoi tesisti e dottorandi, e ora collaboratori. Massimo Cencini e Andrea Puglisi sono ricercatori dell’Istituto dei sistemi complessi del CNR. Cencini si occupa principalmente di turbolenza e fluidodinamica, mentre Puglisi di meccanica statistica di non equilibrio. Il quarto autore è Davide Vergni dell’Istituto per le Applicazioni del Calcolo “Mauro Picone” del CNR. Si occupa di matematica applicata, dai modelli finanziari (modelli di gestione del debito pubblico, in collaborazione con il Ministero del Tesoro) ai sistemi biologici (analisi dei network biologici con applicazioni mediche, in collaborazione con diversi centri di ricerca ospedalieri).
Marco Menale: Ciao, Angelo. Partiamo dal titolo. Perché avete scelto Random Walk?
Angelo Vulpiani: In fisica la random walk (passeggiata aleatoria in italiano) è una semplificazione del moto browniano. Tuttavia con Random Walk intendiamo i possibili percorsi che il libro consente di fare al lettore tra diversi argomenti della fisica e la loro storia. Ciascun percorso definisce una particolare successione dei capitoli. E per questo nelle prime pagine abbiamo inserito un grafo (figura 1) con le possibili scelte. Ma sono da intendersi come suggerimenti. Il lettore può leggere il libro come vuole. Inoltre abbiamo scelto l’ordine alfabetico per i temi dei capitoli così da evitare qualsiasi forma di gerarchia.

Figura 1. Il grafo di alcuni possibili percorsi del libro, da “A Random Walk in Physics”
MM: La prima teoria discussa è l’atomismo. Ed è anche la più antica trattata nel libro, risalendo a personaggi come Democrito e Leucippo. Torna in diversi capitoli, fino a Ludwing Boltzmann. Perché la ritenete così importante?
AV: Ci sono almeno tre motivazione. In primo luogo è una grandiosa teoria che parte da Leucippo e Democrito e arriva fino al CERN. Poi c’è una motivazione personale, in quanto nella storia dell’atomismo ha avuto un ruolo fondamentale Boltzmann, padre fondatore della meccanica statistica, e nostro grande ispiratore. E poi, a parte Boltzmann, c’ è una terza motivazione di natura concettuale. Vogliamo sottolineare l’idea che la scienza non parla solo di descrizioni senza una realtà ultima. A nostro avviso il mondo esiste indipendentemente da noi. E ci rifacciamo a Paul Dirac che iniziava il suo corso di meccanica quantistica dicendo: “si assume che esista un mondo esterno a noi”. Certe volte queste cose vengono dimenticate, eccedendo nel soggettivismo. Chi fa fisica descrive il mondo, cosa esterna a noi. E questo intendiamo sottolineare, ricordando la dura battaglia di Boltzmann contro gli energetisti (qui per approfondire).
MM: Alcuni capitoli riguardano i “problemi del XX secolo”. Scrivete che hanno segnato la fine del determinismo e la nascita della teoria del caos. Siamo in un nuovo paradigma della prevedibilità?
AV: L’insistenza sul caos come nuovo paradigma mi lascia perplesso. Non sono affatto convinto che quella del caos sia la terza rivoluzione del XX secolo, dopo relatività e meccanica quantistica. C’è stata una certa continuità con Poincaré, poi Lyapunov, Wiener, van der Pol, Birkhoff e Kolmogorov, tanto per citarne alcuni. A mio avviso non è corretto dire che negli anni ‘60 c’è stata la scoperta del caos. Piuttosto parlerei di una riscoperta, perché la vera scoperta è di Poincaré. Anche il matematico russo Vladimir Arnold lo dice chiaramente, sostenendo che: “dopo Poincaré non è successo niente”. Tolta qualche ruvidezza di troppo, tipica di Arnold, in qualche modo ha ragione. Ad esempio alcuni si sono riappropriati di vecchie tematiche come la teoria della biforcazione che era già presente nei lavori di Poincaré.
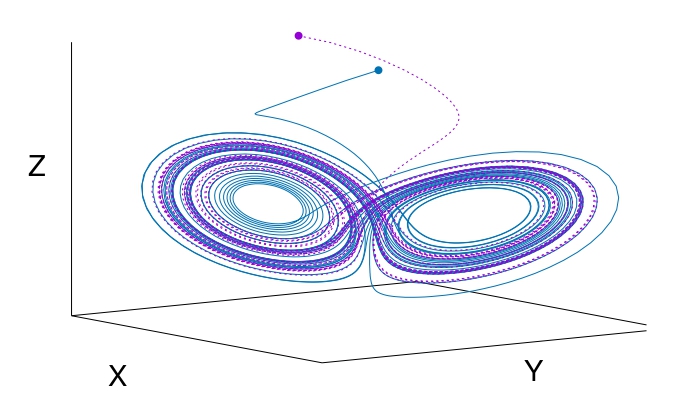
Figura 2. L’attrattore di Lorenz, un primo esempio di modello caotico, da “A Random Walk in Physics”
C’è una cosa interessante della teoria del caos. È stata sviluppata da persone non direttamente coinvolte in problemi fondamentali. Lorenz era un meteorologo, Hénon un astronomo, Chirikov si occupava di macchine acceleratrici. E non sono stati i soli. Consideriamo il caso di Fermi e Heisenberg. Da giovani si sono occupati di meccanica analitica e fluidodinamica, poi hanno fatto il loro grandioso percorso nella fisica moderna per tornare dopo qualche decennio al problema ergodico l’uno con l’esperimento numerico Fermi-Pasta-Ulam-Tsingou e alla turbolenza l’altro.
MM: Nella parte centrale del libro la protagonista diventa la complessità. E lo fate con i modelli, fino a parlare del ruolo degli algoritmi e della teoria dell’informazione. A che punto siamo?
AV: Resto perplesso sull’esistenza di una teoria della complessità come disciplina autonoma. Credo che esistano problemi interessanti in cui ci si deve occupare di vari aspetti della complessità, ma diversi tra loro. Ad esempio nei sistemi dinamici la complessità è temporale, e si possono usare gli esponenti di Lyapunov e l’entropia di Kolmogorov-Sinai. Poi ci sono la complessità algoritmica e quella computazionale. Non credo che queste forme di complessità siano collegate tra loro.

Figura 3. Il volo di uccelli come sistema complesso, da “A Random Walk in Physics”
Alcuni sostengono che esista un punto di collegamento della meccanica statistica con la teoria dell’informazione (qui per approfondire), ma il legame presenta delle debolezze riconducibili al paradosso di Bertrand. Secondo me lo scopo di una disciplina scientifica è tentare di mettere ordine in una fenomenologia, e costruire una teoria. Per questo resto in dubbio riguardo una certa retorica sui sistemi complessi, e una scienza della complessità.
MM: In quest’ottica trattate nel libro i modelli multiscala. Che impatto hanno avuto fino a questo momento? E quali sono le sfide future?
AV: Diversi problemi interessanti presentano una struttura multiscala, dalle proteine al clima. Credo che il primo a trattare sistemi multiscala sia stato Newton con la precessione degli equinozi. Lui l’ha fatto notando che il moto della Luna intorno alla Terra ha un periodo di circa un mese, cioè un tempo molto più breve di quello della precessione, di migliaia di anni. L’idea multiscala per risolvere un problema di questo tipo è semplice, almeno in linea di principio. Ci sono una variabile veloce e una variabile lenta. Faccio una media su quella veloce per avere una descrizione utile del fenomeno che stiamo studiando.
Figura 4. Rappresentazione multiscala, da “A Random Walk in Physics”
In termini moderni, il tipico modello multiscala è l’equazione di Langevin, relativa al moto browniano (qui per approfondire). Un altro esempio è il lavoro di Von Neumann sulle equazioni quasi geostrofiche. I progressi sono lenti, perché i sistemi a multiscala hanno diverse difficoltà. Prendiamo ad esempio il clima, un fenomeno multiscala in cui non ci sono una o più variabili lente e altre veloci, ma tante scale di tempo intermedie. E qui le cose si fanno difficili. Ma le difficoltà sono anche computazionali, perché non posso mettere su un computer questi modelli. Per il clima servirebbe simulare fenomeni da scale di un millimetro e tempi di 1 secondo fino a scale di migliaia di chilometri e tempi di 10.000 anni. E dubito che l’aumento della potenza computazionale possa risolvere il problema.
MM: A un certo punto scrivete di “idee che nascono in un contesto e finiscono in un altro”, come l’equazione di Boltzmann. Credi sia determinato dall’importanza della matematica in fisica?
AV: Effettivamente c’è un’irragionevole efficacia della matematica, come scrive Wigner. L’equazione di Boltzmann, inizialmente introdotta in un ambito puramente teorico della teoria dei gas, ora è usata nella progettazione dei circuiti a semiconduttori e per gli scudi termici delle navicelle spaziali. Forse ancora più sorprendente è l’analisi armonica, che nasce con le serie di Fourier introdotte nell’ambito dell’equazione del calore, e ha poi acquisito una sua autonomia. E oggi le serie di Fourier le troviamo in svariati ambiti, come il funzionamento di una TAC.

Figura 5. L’evoluzione di un gas alla base dell’equazione di Boltzmann, da “A Random Walk in Physics”
Si assiste spesso a questo passaggio delle idee da un contesto all’altro. Pensiamo allo stato solido. Negli anni ‘20 era quasi un esercizio di meccanica quantistica, mentre ora è alla base della moderna tecnologia. La stessa meccanica quantistica è nata per spiegare fenomeni marginali, come lo spettro del corpo nero. E da queste domande è nata una teoria di grande successo, con applicazioni sempre più impattanti sulle nostre vite. Qualche tempo fa mi sono operato di cataratta. Grazie alle nuove tecnologie laser la durata dell’intervento è stata di pochi minuti, mentre prima serviva addirittura il ricovero. E questo progresso lo si deve anche alla meccanica quantistica.
MM: Nel libro dite che “fare previsioni solo con i dati non è sperabile”. Quindi i Big Data non soppianteranno i modelli?
AV: Parto da un presupposto: i Big Data è meglio averli che non averli. È come dire: meglio avere la Trasformata di Fourier che no. Tuttavia con la sola Trasformata di Fourier non puoi sperare di risolvere tutti i problemi della matematica. Per i Big Data vale qualcosa di simile. Possono essere utili per problemi molto pratici, ad esempio l’organizzazione ottimale di un magazzino. Però non credo si possa fare scienza di base con i Big Data, almeno per ora non è successo.
Ricordo un entusiasmo simile sui dati negli anni ’80 dopo un lavoro di Takens sulla ricostruzione dello spazio delle fasi. Si trovava un modo di trattare i dati di laboratorio con i concetti della teoria dei sistemi dinamici. Un risultato bello e importante. Tuttavia la gente all’inizio non aveva capito che ci fosse un limite. Era il problema della dimensionalità. Se il sistema ha una dimensione alta, diciamo oltre 5 o 6, il metodo non funziona più. Su questo punto ha fatto chiarezza un articolo di David Ruelle: “per campionare un insieme di dimensione D serve un numero di punti che cresce con l’esponenziale di D”. E quel primo entusiasmo svanì. Ma sembra che questa storia sia stata dimenticata.
MM: La parte finale del libro è rivolta a entropia e irreversibilità. Perché hanno ruolo così importante?
AV: Sono due aspetti tecnici, ma di grande peso. Tuttavia qualche volta confondono le idee. Ci sono diverse definizioni di entropia. La prima è termodinamica, poi c’è un’entropia alla Shannon per la teoria dell’informazione e quella di Kolmogorov-Sinai per i sistemi dinamici. Queste entropie in parte sono collegate, ma non necessariamente. Una cosa ce l’hanno in comune, sono tutte contatori logaritmici, ossia contano la proliferazione esponenziale di qualcosa.
In meccanica statistica l’entropia conta le configurazioni, mentre l’entropia di Kolmogorov-Sinai il numero di traiettorie con una certa precisione. Insistiamo molto sull’irreversibilità per ricordare Boltzmann che aveva capito tutto nella sostanza. Tuttavia alcuni l’hanno esplicitamente calunniato, come Ilya Prigogine, ispiratore di un filone post-moderno che vuole rivedere il punto di vista di Boltzmann (qui per approfondire). A parte gli aspetti tecnici, il punto importante di questi due elementi è l’enorme numero di gradi di libertà. E un’altra cosa importante è la selezione della condizione iniziale. Oscar Lanford ha dimostrato che è sufficiente scartare alcune condizioni iniziali che portano a situazioni paradossali (qui per i dettagli). La cosa importante è che la probabilità di avere comportamenti anti-entropici sia piccolissima (trascurabile a tutti gli effetti) su tempi lunghi e nei sistemi macroscopici.
MM: Per voi le invenzioni portano di solito il nome di un’unica persona che si prende tutti i meriti. Eppure dedicate alcuni capitoli a singoli scienziati, come Boltzmann e Einstein. Come vedi il bilancio tra contributi individuali e progresso scientifico? Quanto contano alla fine i singoli scienziati?
AV: La Scienza è un’impresa collettiva. Tuttavia ci sono personaggi che danno contributi più importanti. Anche grandi personalità potrebbero non essere state così determinanti. Prendiamo l’esempio di Einstein. La relatività ristretta era nell’aria, grazie tra gli altri a Poincaré. Se Einstein non fosse mai nato, probabilmente la relatività ristretta ci sarebbe stata ugualmente. Alcuni hanno sostenuto che se Maxwell non fosse morto giovane, l’avrebbe fatta lui. Mentre la relatività generale è stata formulata grazie a Einstein. È un’idea sua, forse sarebbe venuta fuori ugualmente ma chissà quando.

Figura 6. Rappresentazione di un moto browniano, da “A Random Walk in Physics”
E poi serve fortuna. Consideriamo ancora Einstein, ma questa volta per il suo lavoro sul moto borwniano. Lui non era un esperto di moto browniano, eppure è il suo nome a essere passato alla storia. Prima di lui il fisico polacco Marian Smoluchowski aveva fatto esperimenti ed elaborato una teoria generale ed elegante. Purtroppo per lui è morto giovane e i meriti sono andati tutti a Einstein. Per questo resto convinto che la scienza sia un’impresa collettiva, con delle punte di valore.

A Random Walk in Physics: Beyond Black Holes and Time-Travels
M. Cencini, A. Puglisi, D. Vergni, A. Vulpiani
Editore: Springer Nature
Anno edizione: 2021
Pagine: 224 p.



















