Una mini-serie a cura di Marco Trombetti, in cui si esploreranno la tumultuosa storia e le incredibili vette raggiunte dalla matematica delle simmetrie: la teoria dei gruppi. In questo quinto episodio ci addentriamo sempre di più nei risultati che hanno fatto la storia della teoria dei gruppi, prendendo ancora una volta spunto da una vicissitudine postuma di Alfredo Capelli.

 

Bentornati. Siamo qui riuniti questa volta per parlare di un caso di mal attribuzione decisamente più grave di quello della scorsa puntata. Parliamo dell’argomento di Frattini.

 

Chi era Giovanni Frattini?

Giovanni Frattini nasce a Roma l’otto gennaio del 1852. Sì iscrive nel 1869 alla facoltà di matematica dell’Università di Roma, e vi si laurea nel 1875 sotto la supervisione di Giuseppe Battaglini (lo stesso supervisore di Alfredo Capelli!). Nell’ottobre del 1876 inizia la sua carriera come insegnante di scuola secondaria. Le sue eccellenti doti di insegnante lo resero presto uno tra i più stimati insegnanti dell’epoca. Frattini si ritirò dall’insegnamento nel 1921 e morì il 21 luglio del 1925.

 

Cos’è l’argomento di Frattini?

Come dice il nome, l’argomento di Frattini è nient’altro che un argomento dimostrativo molto versatile ed utile in teoria dei gruppi. Abbiamo già osservato nello scorso episodio che il secondo teorema di Sylow assicura che i sottogruppi di Sylow sono coniugati tra di loro. Cerchiamo di capire ora cosa vuol dire che due sottogruppi $H$ e $K$ di un gruppo $G$ siano coniugati. Essenzialmente vuol dire che esiste un elemento $x$ del gruppo $G$ che ‘‘applicato’’ ad $H$, sposti $H$ su $K$.

Cosa intendo con applicato? Non è necessario saperlo per i nostri fini, però per i più curiosi voglio dire che l’insieme $x^{-1}Hx=\{x^{-1}\cdot h\cdot x\,:\, h\in H\}$ viene a coincidere con $K$. In questo senso l’elemento $x$ agisce su i sottogruppi spostandoli, permutandoli. Ciò che è veramente necessario sapere è che questo spostamento preserva tutte le proprietà del sottogruppo, ad esempio l’ordine.

Ora, in poche parole, l’argomento di Frattini consiste nell’applicare un’azione di coniugio da due punti di vista diversi, che io direi ‘‘dall’interno’’ e ‘‘dall’esterno’’. Mi spiego meglio. Consideriamo il gruppo simmetrico $S_4$ su i quattro numeri $1,2,3,4$ (cioè l’insieme delle permutazioni di questi quattro numeri con la composizione), e il suo sottogruppo $A_4$. Come abbiamo già avuto modo di osservare, l’ordine di $S_4$ è $4!=24$, mentre l’ordine di $A_4$ è $12$. Ora, $3$ è la massima potenza di $3$ che divide $12$, ma è anche la massima potenza di $3$ che divide $24$. Dunque, $A_4$ contiene un sottogruppo di Sylow $P$  di ordine $3$ (per il primo teorema di Sylow), e tale sottogruppo è anche un sottogruppo di Sylow di $S_4$.

A questo punto, se $x$ è un qualunque elemento di $G$, allora l’azione di $x$ su $P$ lo sposta in un altro sottogruppo di Sylow di ordine $3$, chiamiamolo $P^x$ (questa è l’azione dall’esterno). Poiché $A_4$ risulta essere un punto fisso dell’azione di $x$ (è difatti un tipo di sottogruppo molto speciale, detto ‘‘normale’’), cioè non viene spostato, allora $P^x$ è ancora contenuto in $A_4$. Dunque ora abbiamo due sottogruppi di Sylow di ordine $3$ di $S_4$ che sono contenuti in $A_4$. A questo punto entra in gioco il secondo teorema di Sylow che ci assicura che esiste un elemento $y$ di $A_4$ che (ri)sposta $P^x$ in $P=P^{xy}$ (questa è l’azione dall’interno).

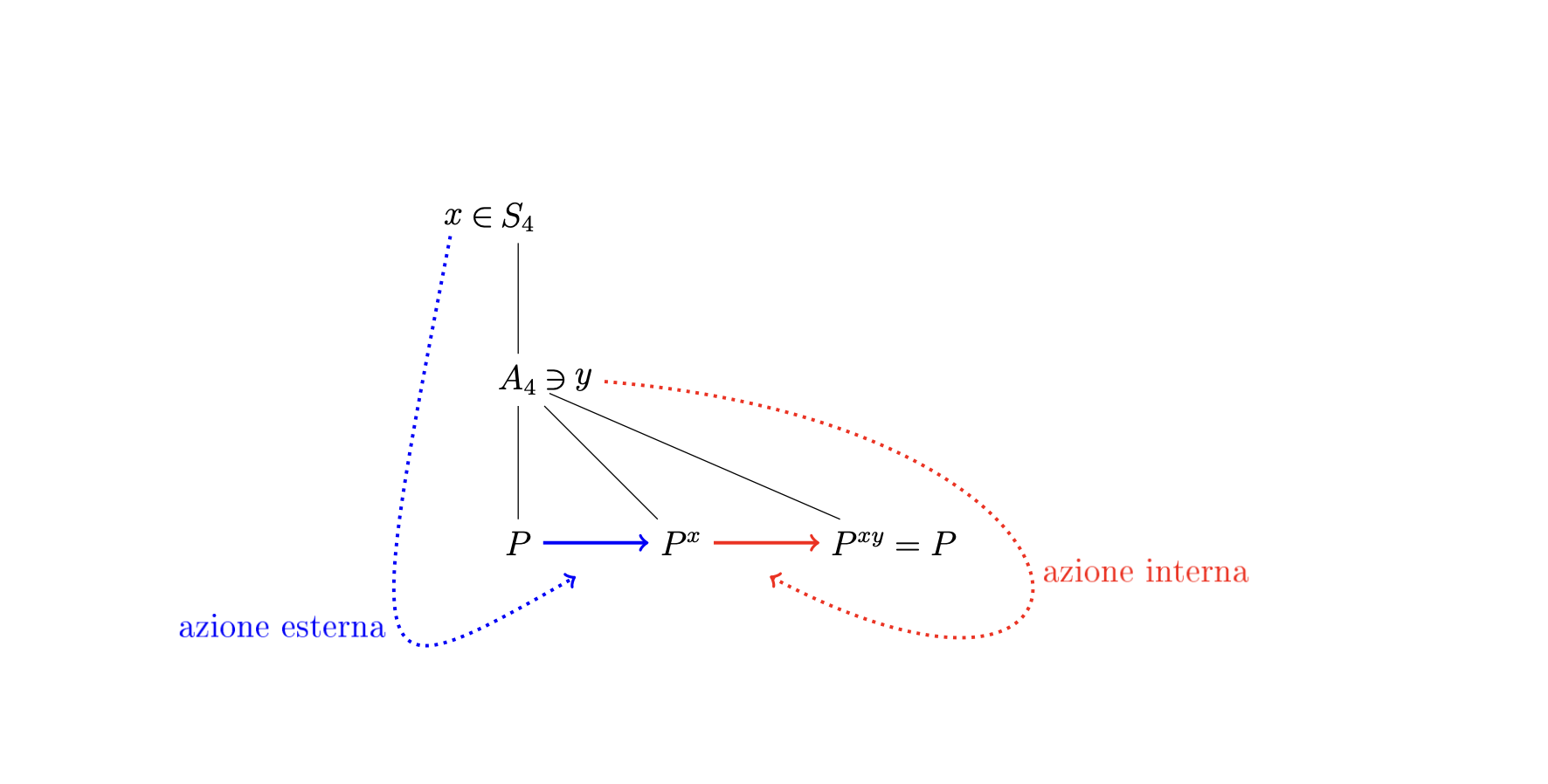
Questo è l’argomento di Frattini, facile no?

Per quanto facile ha però una serie di conseguenze notevolissime. L’importanza di un risultato si giudica spesso dalle sue conseguenze. E l’argomento di Frattini permette ad esempio di dimostrare (ed è stato usato da Frattini per dimostrare) che un sottogruppo notevole (che oggi viene chiamato sottogruppo di Frattini) è nilpotente (cioè, ha una proprietà molto molto buona!) nel caso dei gruppi finiti. Ma non solo, il lettore potrà comprendere l’importanza di tale argomento dal solo fatto che vi sia stata la necessità di dargli un nome! Un fenomeno questo abbastanza raro in matematica, e che accade solo quando c’è un argomento il cui uso è veramente frequente e ha bisogno di essere richiamato spesso dagli esperti del settore senza troppi fronzoli.

 

 

Come entra in gioco Capelli?

L’articolo di Frattini in cui per la prima volta appare l’argomento è del 1885 e si intitola: Intorno alla generazione dei gruppi di operazioni. Nell’articolo però Frattini scrive che prima di provare il teorema in cui usa l’argomento, deve necessariamente notare che tale argomento è dovuto a Capelli. In effetti Capelli usa per la prima volta (e per ben due volte) l’argomento di Frattini nel 1884 in un articolo che si intitola: Sopra la composizione dei gruppi di sostituzione.

Quindi Frattini riconosce a Capelli la paternità dell’argomento. Ma allora perché la maggior parte dei gruppisti continua a riferirsi a tale argomento come ‘‘di Frattini’’? Beh, la risposta è semplice: si è probabilmente trattato di un errore fatto da grandi e stimatici matematici non-italiani dell’epoca. E il non-italiani è fondamentale, perché la nota di Frattini era in italiano, quindi è plausibile che non si siano accorti dell’attribuzione che Frattini faceva dell’argomento a Capelli.

C’è però una critica che si può muovere a questa motivazione: perché la nota di Frattini era nota anche al di fuori dell’Italia mentre quella di Capelli no? La risposta a questa domanda è meno scontata, e ha a che fare con Eugen Netto (altro matematico di cui avevamo già parlato e che aveva anch’esso riscoperto i teoremi di Sylow). Poiché leggere ogni volta articoli di matematica è un passatempo non poco dispendioso, e poiché ci sono tantissimi articoli di matematica, è pratica comune (ancora oggi) per i matematici che prima di iniziare la lettura di un articolo, si leggano le recensioni che sono state fatte al riguardo.

Avete capito bene, anche la matematica fa affidamento sulle recensioni! E come accade ancora oggi, qualche volta queste recensioni non sono proprio affidabilissime. La recensione del lavoro di Capelli fu fatta da Eugen Netto (vedi Jahrbuch über die Fortschritte der Mathematik XVI, p. 116), e in quella recensione Netto ha attribuito a Capelli un teorema evidentemente non corretto (che non era presente nell’articolo) probabilmente per una svista. Ma a causa dell’autorità di Netto questo ha contribuito grandemente a far si che l’articolo di Capelli fosse ignorato dai più. Ad onor di cronaca va anche notato che sviste simili di Netto possono trovarsi in recensioni ad alcuni lavori di Camille Jordan e Ludwig Sylow.

 

Gli $\Omega_0$-gruppi di Capelli e il sottogruppo di Frattini

In questa sezione voglio ancora tessere le lodi di Capelli portando un altro esempio in relazione all’argomento di Frattini. Abbiamo già osservato che tale argomento ci permette di dimostrare che il sottogruppo di Frattini di un gruppo finito è nilpotente. Vediamo ciò cosa vuole dire.

Un gruppo finito è nilpotente se per ogni primo che divide il suo ordine esiste esattamente un solo sottogruppo di Sylow relativo a quel primo. Ad esempio, dall’inverso forte del teorema di Lagrange (che abbiamo visto nell’episodio precedente) segue che i gruppi ciclici finiti sono nilpotenti. In realtà, più in generale tutti i gruppi finiti abeliani (cioè in cui l’operazione sia commutativa) sono nilpotenti. Tali gruppi si ‘‘spezzano’’ nel prodotto (diretto) dei loro (unici) sottogruppi di Sylow ed è quindi sufficiente poi studiare singolarmente questi per ottenere la struttura del gruppo. In ogni caso, la loro struttura è considerata particolarmente buona è spesso nel dimostrare i teoremi si è soddisfatti se si riesce ad arrivare al punto che qualcosa sia nilpotente.

Vediamo esempi di gruppi che nilpotenti non sono. Sicuramente tra questi possiamo annoverare tutti i gruppi simmetrici e alterni di grado maggiore o uguale a tre. Ma andiamo più nel dettaglio e consideriamo il gruppo delle simmetrie del triangolo equilatero che ha ordine $6$. Tale gruppo non è nilpotente perché non c’è un solo sottogruppo di Sylow di ordine $2$. Infatti ce ne sono ben quattro e possono essere costruiti mettendo insieme l’identità e un qualsiasi ribaltamento.

Cos’è invece il sottogruppo di Frattini di un gruppo finito $G$? Beh, è semplicemente l’intersezione di tutti i sottogruppi massimali del gruppo, cioè l’intersezione di tutti i sottogruppi di $G$ che sono diversi da $G$ e non sono contenuti in nessun altro sottogruppo diverso da $G$. Notiamo esplicitamente qui che l’intersezione di sottogruppi è un sottogruppo.

Facciamo un esempio. Nel caso del gruppo delle simmetrie del triangolo equilatero, il sottogruppo delle rotazioni è un sottogruppo massimale. Per vederlo, basta notare che il suo ordine è $3$ e che un sottogruppo di ordine più grande, dovendo andare a dividere $6$ (per il teorema di Lagrange), deve necessariamente avere ordine $6$ e quindi coincidere con tutto il gruppo ambiente. In maniera simile, il sottogruppo di ordine $2$ che abbiamo costruito a suo tempo è anch’esso un sottogruppo massimale per motivi simili a quelli di prima. E qual è la loro intersezione? Poiché l’intersezione di sottogruppi è un sottogruppo, allora per il teorema di Lagrange l’ordine dell’intersezione deve dividere sia $2$ che $3$ e quindi per forza di cose deve essere $1$. Poiché un gruppo ha un solo sottogruppo di ordine uno (cioè il sottogruppo banale fatto dall’elemento neutro), allora il sottogruppo di Frattini contiene solamente l’identità.

Nel suo articolo, Frattini denota questo sottogruppo con $\Phi(G)$ (sarà un caso?) e dimostra che tale sottogruppo è (nel gergo dell’epoca) ‘‘eccezionale’’. Nel terminologia odierna diremo semplicemente che $\Phi(G)$ è normale. Dopo aver dimostrato dunque la normalità del suo sottogruppo, Frattini dimostra che è nilpotente, ma non usa il termine nilpotente. Il termine che usa per descrivere la proprietà di nilpotenza che abbiamo descritto sopra è: $\Omega_0$-gruppo di Capelli. Cioè, Frattini attribuiva la paternità del concetto di nilpotenza (nel caso dei gruppi finiti quantomeno) ad Alfredo Capelli! Eppure tale concetto è spesso accreditato solo a Sergey Chernikov (~1930).

 

 

Conclusioni

A questo punto spero che questi due episodi consecutivi sulle vicissitudini di Capelli possano in qualche modo contribuire alla rivalutazione del suo lavoro. Sicuramente sarebbe opportuno e auspicabile che l’argomento di Frattini iniziasse ad essere chiamato dai più argomento di Capelli, o almeno argomento di Capelli-Frattini. Noi ci vediamo al prossimo episodio per scoprire come vincere una medaglia Fields in teoria dei gruppi!

 

Referenze

1. M. Brescia, F. de Giovanni, e M. Trombetti: ‘‘The true story behind Frattini’s Argument’’, Adv. Group Theory Appl. 3 (2017), 117-129.
2. G.A. Miller: “Group theory reviews in the Jahrbuch über die Fortschritte der Mathematik”, Bull. Amer. Math. Soc. 27 (1921), 459–462.