Una mini-serie a cura di Marco Trombetti, in cui si esploreranno la tumultuosa storia e le incredibili vette raggiunte dalla matematica delle simmetrie: la teoria dei gruppi. In questo quarto episodio entreremo un po’ più nel vivo della teoria dei gruppi con l’ausilio di una figura che in teoria dei gruppi non ha mai avuto riconosciuti i meriti che gli spettavano.

Probabilmente, gran parte dei lettori nel leggere il titolo avrà già individuato e legato il nome di Alfredo Capelli al famoso teorema di Rouché-Capelli riguardante la risoluzione dei sistemi di equazioni lineari. Tale teorema usa essere studiato ad esempio nei corsi di “Algebra e Geometria” di buona parte delle ingegnerie italiane, ed è fondamentale per gli sviluppi successivi. Pochi sanno però che Capelli fu anche gruppista in senso stretto, e che diede contributi di grande rilievo nell’ambito della teoria dei gruppi. Purtroppo, come vedremo in questa e nella prossima puntata, la storia ha voluto che tali contributi si svincolassero dal suo nome e finissero con l’essere associati quasi esclusivamente ad altri. Da qui il gioco del titolo.

Solo molto a posteriori si è tentato di riportare alla ribalta postuma l’opera di Alfredo Capelli (vedi ad esempio Casadio, Zappa: ‘‘I contributi di Alfredo Capelli alla teoria dei gruppi’’, Boll. Stor. Sci. Mat. (2) 11 (1991), 25-54) ma mi sento di dire (da insider) che probabilmente non è stato fatto ancora abbastanza. La mia speranza con questi due episodi successivi è di aiutare in questo proposito.

Prima di iniziare però voglio condividere con voi una piccola curiosità sul teorema di Rouché-Capelli. Tale risultato è difatti noto con questo nome in tutti gli stati di lingua inglese, italiana, e in Brasile, mentre negli stati russofoni è noto come teorema di Kronecker-Capelli, in Francia come teorema di Rouché-Fontené, in Spagna e America Latina come teorema di Rouché-Frobenius. Quindi anche per quanto concerne questo famosissimo teorema, il suo nome va a sparire, sebbene fortunatamente solo in una manciata di stati.

 

Chi era Alfredo Capelli?

Alfredo Capelli nasce a Milano nel 1855 (quindi prima dell’unità d’Italia). Frequentando l’università di Roma, finirà con il seguire un corso di Giuseppe Battaglini nell’anno accademico 1875/76 sulla teoria dei gruppi di sostituzioni basato su un famosissimo trattato di Camille Jordan dell’epoca: Traité des substitutions et des équations algebraique. Questo trattato contiene tutta la teoria di Galois nota all’epoca ed è praticamente il primo libro di teoria dei gruppi al mondo: si può senz’altro dire che fu grazie a questo trattato che la teoria dei gruppi fiorì incredibilmente nei successivi 100 anni.

Inizia così l’avventura del giovane Capelli nella teoria dei gruppi, seguito da Battaglini. Non molto tempo dopo, e precisamente nel 1878, Capelli pubblicherà un articolo di 55 pagine in teoria dei gruppi che avrebbe decisamente avuto la forza di scuotere l’intero settore.

In questo articolo Capelli dimostra (tra le altre cose) i teoremi di Sylow, il teorema di Jordan sulle serie di composizione, e alcuni (oggi standard) risultati di teoria dei gruppi che sono stati successivamente riscoperti da Frobenius e Burnside, e che oggi portano il loro nome. Per quanto riguarda però i teoremi di Sylow (quello che ci interessa qui), questi erano già stati provati nel 1872 da Ludwig Sylow e (riscoperti) nel 1874 da Eugen Netto. D’altro canto la dimostrazione di Capelli è decisamente più semplice di quelle di Sylow e Netto. Il mondo dell’epoca non era così collegato come lo è oggi, e Capelli era totalmente ignaro del fatto che alcuni suoi risultati fossero ‘‘noti’’, così come anche Frobenius e Burnside saranno successivamente ignari di quanto provato da Capelli.

Dopo essere divenuto professore a Palermo nel 1881, si spostò ancora nell’1886 all’Università degli Studi di Napoli Federico II, dove ottenne la cattedra in algebra. Rimase a Napoli fino alla morte, avvenuta nel 1910.

 

I teoremi di Sylow

L’importanza che tali teoremi rivestono all’interno della teoria dei gruppi può essere dedotta dal fatto che nel corso del tempo si sono avvicendate tantissime dimostrazioni diverse di questi teoremi (con le più svariate tecniche). Nostro compito sarà solo però spiegare cosa sono questi teoremi e perché sono così importanti, per la storia delle loro dimostrazioni rimandiamo a (Casadio – Zappa: ‘‘Storia del teorema di Sylow e delle sue dimostrazioni’’, Boll. Stor. Sci. Mat. (1) 10 (1990), 29-73).

Prima ancora di poterci addentrare nell’enunciato dei teoremi di Sylow, dobbiamo parlare di cosa sono i ‘‘sottogruppi’’ di un gruppo. Arrivati a questo punto il lettore saprà almeno a grandi linee cos’è un gruppo, cioè un insieme $G$ munito di una operazione interna $\cdot$ che soddisfa le 3 proprietà che abbiamo visto: associatività, esistenza dell’elemento neutro, e esistenza degli inversi.

Esempi di gruppi che abbiamo già incontrato sono i gruppi simmetrici e i gruppi alterni. Prediamo ad esempio il gruppo simmetrico $S_3$ su tre oggetti (ricordo che è il gruppo di tutte le possibili permutazioni dei numeri $1,2,3$) e il gruppo alterno $A_3$ (cioè il gruppo di tutte le possibili permutazioni dei numeri $1,2,3$ che sono costruibili mediante un numero pari di scambi di due elementi). Non molto sorprendentemente, $A_3$ è un sottogruppo di $S_3$. Più in generale un sottogruppo di un gruppo $G$ è un sottoinsieme $H$ che risulti essere un gruppo con l’operazione di $G$ ristretta ad $H$. Nel caso di $S_3$, l’operazione è l’eseguire due permutazioni in successione (la composizione, in gergo), e poiché la composizione di due permutazioni pari è pari, allora l’operazione di $S_3$ si può restringere all’insieme delle permutazioni pari.

Non basta solo questo però! Bisogna poi effettivamente verificare che il sottoinsieme $A_3$ sia un gruppo, e cioè che l’operazione ristretta soddisfi agli assiomi di gruppi: l’associatività è praticamente gratis, l’esistenza dell’elemento neutro la si ha perché la permutazione identica è pari, e gli inversi di permutazioni pari è facile accorgersi che sono pari.

Questo esempio può essere visto in termini di simmetrie come segue. Prendiamo di nuovo in considerazione l’insieme di tutte le simmetrie del triangolo equilatero.

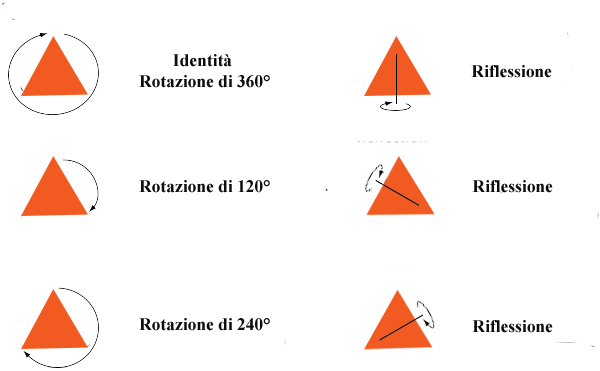
Se andiamo a considerare il sottoinsieme costituito solo dalle rotazioni, cioè dalle tre simmetrie nella prima colonna, questo sarà un sottogruppo del gruppo delle simmetrie del triangolo equilatero. Difatti, componendo due rotazioni, si ottiene ancora una rotazione. L’inversa di una rotazione è una rotazione, e l’identità è la rotazione di 0° o di 360°. Vedendolo in questo modo ci si accorge subito che ci sono anche altri sottogruppi. Ad esempio, consideriamo l’insieme fatto dalle simmetrie sulla prima riga, cioè l’identità e la riflessione rispetto all’asse verticale. Questo è ancora un sottogruppo.

Per vederlo, diamo dei nomi agli oggetti, chiamiamo l’identità $Id$ e la riflessione $\tau$. Dobbiamo verificare che comunque vada a comporre queste due mappe, il risultato sia ancora una di queste. Così, ad esempio $\tau\cdot\tau=Id$ e $\tau\cdot Id=\tau$. Questo ci dice anche che l’inversa di $\tau$ è essa stessa. Dunque questo sottoinsieme è un sottogruppo con due oggetti (è un gruppo ciclico di ordine $2$).

Se invece andiamo a considerare l’insieme fatto dall’identità e dalla rotazione (in senso orario) di 240°, questo non è un sottogruppo. Infatti, se andiamo a comporre la rotazione di 240° con sé stessa, otteniamo la rotazione di 480°, che coincide con la rotazione di 120°, che non è contenuta nell’insieme in questione.

Vediamo ancora un altro esempio, questa volta tratto dall’ambito numerico. Consideriamo l’insieme dei numeri reali $(\mathbb R,+)$ munito dell’addizione. Il sottoinsieme dei numeri razionali $(\mathbb Q,+)$ è un sottogruppo in questo caso, perché la somma di due numeri razionali è razionale, l’opposto di un numero razionale è razionale e $0$ è un numero razionale (il lettore avrà sicuramente notato che in tutti gli esempi di sottogruppi, l’elemento neutro del gruppo di partenza appartiene al sottogruppo, e gli opposti sono gli stessi, sarà un caso?). Similmente, $(\mathbb Z,+)$ (l’insieme dei numeri interi) è un sottogruppo di $(\mathbb Q,+)$ e quindi un sottogruppo di $(\mathbb R,+)$ (per i sottogruppi vale la proprietà transitiva). Ma, $(\mathbb N,+)$, l’insieme dei numeri interi non-negativi, non è un sottogruppo, perché ad esempio l’opposto di $3$ (cioè $-3$) non appartiene a $(\mathbb N,+)$.

 

Perché è importate conoscere i sottogruppi di un gruppo?

L’importanza di questo fatto deriva dalla seguente osservazione. Esistono gruppi così grandi la cui struttura è difficilmente comprensibile. Un modo allora per poter comprendere tali gruppi è considerare i sottogruppi propri (cioè diversi dal gruppo stesso) e vedere come si comportano questi (all’interno del gruppo). Spesso e volentieri questi sottogruppi sono più facili da gestire, poiché più piccoli del gruppo stesso. Ad esempio, nel caso del gruppo delle simmetrie del triangolo equilatero si scopre facilmente che il sottogruppo delle rotazioni è l’unico sottogruppo di ordine $3$, e questo comporta tutta una serie di informazioni interessanti (se a priori non sapessimo già com’è fatto il gruppo da cui siamo partiti, permetterebbe di ridurne grandemente lo studio).

Inoltre, lo studio dei sottogruppi aiuta ad applicare uno dei metodi dimostrativi classici in matematica: il cosiddetto principio di induzione. Supponi di avere una proprietà che vuoi provare per tutti i gruppi finiti. Se riesci a far vedere che questa proprietà vale per i gruppi di ordine $n$ ogni volta che vale per tutti i gruppi di ordine strettamente più piccolo di $n$, allora avrai dimostrato la proprietà per tutti i gruppi finiti.

 

 

Il teorema di Lagrange e sue inversioni

Per quanto riguarda i gruppi finiti, ad esempio il gruppo delle simmetrie del triangolo equilatero visto sopra, si può dimostrare qualcosa di molto affascinante. Cioè la grandezza di un sottogruppo deve necessariamente essere un divisore dell’ordine del gruppo. Nell’esempio citato, che ha ordine $6$, abbiamo trovato due sottogruppi di ordini rispettivamente $2$ e $3$, che non a caso sono divisori di $6$. Questo è un fatto generico: ogni volta che abbiamo un gruppo finito di ordine $n$, e un suo sottogruppo di ordine $m$, allora $m$ deve dividere $n$.

Tale risultato è usualmente attributo a Lagrange (sì, proprio quello dell’analisi), ma Lagrange ne dimostrò solo un caso particolare nel 1771. Dopo altri contributi parziali di Gauss (1801) e Cauchy (1844), il risultato ci è pervenuto nella sua forma attuale grazie a Camille Jordan (1861). Un altro caso di mal attribuzione?

Ad ogni modo, tale risultato è importantissimo perché ci dice immediatamente ad esempio che comunque vi scegliate $5$ simmetrie del triangolo equilatero queste non formeranno mai un (sotto)gruppo!

Ancora più interessante è però il problema inverso. Esiste per ogni divisore dell’ordine del gruppo almeno un sottogruppo che abbia quell’ordine?  Nel caso delle simmetrie del triangolo equilatero abbiamo già dimostrato che la risposta è sì, perché abbiamo esibito due sottogruppi, uno di ordine $2$ e uno di ordine $3$. Inoltre il gruppo stesso può essere considerato un sottogruppo di ordine $6$, e il sottoinsieme formato solo ed esclusivamente dall’identità è facile vedere sia un sottogruppo di ordine $1$. Quindi tutti i divisori dell’ordine del gruppo (cioè i divisori di $6$) danno luogo ad almeno un sottogruppo.

Non è sempre così. Ad esempio, nel gruppo alterno $A_4$, che ha ordine $12$, mancano sottogruppi di ordine $6$.

Una risposta positiva all’inverso del teorema di Lagrange fa spesso la differenza. Molti gruppi la cui struttura è considerabile ‘‘buona’’ (ad esempio gruppi abeliani, risolubili e nilpotenti) ammettono una risposta positiva a tale problema, e anzi per i gruppi ciclici finiti vale anche qualcosa di più sorprendente. Sì può infatti dimostrare che per ogni divisore dell’ordine di un gruppo ciclico finito non solo esiste un sottogruppo di quell’ordine ma questo è unico! (cosiddetto inverso forte del teorema di Lagrange) In effetti, i gruppi ciclici sono tra le tipologie di gruppi più maneggiabili all’interno della teoria dei gruppi.

 

I teoremi di Sylow

Torniamo finalmente su i teoremi di Sylow. Con tale terminologia si designano $3$ teoremi che valgono per i gruppi finiti e che riguardano l’esistenza di determinati sottogruppi speciali e le loro proprietà.

Il primo teorema di Sylow

Sia $G$ un gruppo (arbitrario) finito di ordine $28$.  Il primo teorema di Sylow afferma (in una delle sue forme) che per ogni primo che divide l’ordine del gruppo esiste almeno un cosiddetto sottogruppo di Sylow, cioè un sottogruppo il cui ordine è la massima potenza di quel primo che divide l’ordine del gruppo. Nell’esempio in questione, poiché $4$ è la massima potenza del primo $2$ che divide $28$, allora esisterà almeno un sottogruppo di ordine $4$. Similmente, poiché $7$ è la massima potenza del primo $7$ a dividere $28$, ciò vorrà dire che esisterà un sottogruppo di ordine esattamente $7$.

Una conseguenza rilevante del primo teorema di Sylow è che per ogni potenza di primo che divide l’ordine del gruppo esiste un sottogruppo di quell’ordine. Così ad esempio nel gruppo arbitrario di prima di ordine $28$ non solo esisteranno sottogruppi di ordine $4$ ma anche di ordine $2$.

Se pensiamo all’esempio del gruppo delle simmetrie del triangolo equilatero, i due sottogruppi che abbiamo fornito sono esattamente due sottogruppi di Sylow, uno di ordine $2$ e l’altro di ordine $3$. Il teorema di Sylow fornisce il miglior risultato di inversione del teorema di Lagrange.

Il secondo teorema di Sylow

Questo secondo risultato viene a dirci che tutti i sottogruppi di Sylow di uno stesso ordine sono coniugati. Non ha tantissima importanza al momento sapere cosa questo voglia dire, ma vi basti sapere che ciò a grandi linee vuol dire che in qualche senso i sottogruppi di Sylow di uno stesso ordine si comportano esattamente nella stessa maniera.

Tale risultato ha due interessanti corollari. Prima di tutto ci dice che il numero di sottogruppi di Sylow di un dato ordine è un divisore dell’ordine del gruppo. Ci dice inoltre che quando esiste un unico sottogruppo di Sylow di un dato ordine (come ad esempio nel caso del gruppo delle simmetrie del triangolo equilatero), allora questo sottogruppo gode di una proprietà molto speciale: è normale (vedremo in seguito cosa vuol dire).

Il terzo teorema di Sylow

Tale teorema ci fornisce una ulteriore indicazione sulla quantità di sottogruppi di Sylow di un dato ordine. Questo afferma che il numero dei sottogruppi di Sylow che sono potenza di un dato primo $p$ è uguale ad $1$ modulo $p$. Quindi ad esempio nel caso di un gruppo di ordine $28$, il numero $n_7$ dei Sylow di ordine $7$ deve essere uguale a $1$ modulo $7$. Di conseguenza, le uniche possibilità sono $n_7=1,8,15,\ldots$. Ricordando però che come conseguenza del seconda teorema di Sylow, il numero $n_7$ deve dividere l’ordine del gruppo, abbiamo che l’unica possibilità è allora $n_7=1$. Dunque, senza neanche sapere come sia fatto il gruppo, abbiamo dedotto che c’è un unico sottogruppo di ordine $7$.

 

Che cosa incredibile! Devo aggiungere altro? Ci vediamo alla prossima puntata.