Se volete ordinare una pizza con degli amici per dividerla con loro, assicuratevi prima che tra loro non ci sia uno dei matematici della “teoria della pizza”. Essi potrebbero essere molto più desiderosi di esplorare le  varie possibilità di taglio della pizza che darvi il solito spicchio. In quel caso quindi, tagliare e mangiare la pizza potrebbe essere molto più complicato del previsto!

 Per apprezzare l’entusiasmo di questo gruppo di ricercatori, se non l’utilità dei risultati dimostrati, si può dare un’occhiata a un documento pubblicato su arXiv da Joel Haddley e Stephen Worsley del Dipartimento di Scienze Matematiche dell’Università di Liverpool.

Il documento è intitolato “Famiglie infinite di tassellature a disco monoedrico” ed in esso esporano proprio il problema applicato al taglio di una pizza.

Per capire come la pizza gioca un ruolo nel loro articolo, si può partire dalla definizione di tassellatura monoedrica. Gli autori hanno scritto nel loro articolo: “Un set di piastrelle di una forma planare si chiama monoedrica se tutte le tessere della tassellatura sono congruenti tra di loro. Tali tassallature, se applicate al disco, sono prodotte quotidianamente da tutti i pizzaioli… prendendo tagli radiali distribuiti uniformemente attorno al centro della pizza, ovvero tagliando la pizza in modo classico. ”

Jacob Aron ha osservato che “la maggior parte di noi divide la pizza con tagli rettilinei che si incontrano nel mezzo. Ma cosa succede se il centro della pizza ha un condimento che alcune persone preferiscono evitare, mentre altri deriderano di più mangiare la crosta?”

È proprio in situazioni come questa che arriva l’aiuto della matematica. In passato, altri lavori scientifici avevano già formalizzato una configurazione per creare dodici pezzi di forma uguale, sei dei quali formano una stella che parte dal centro e altri sei corrono lungo il bordo:

 

 

 

 

 

 

“Si inizia tagliando a fette a tre lati curvi attraverso la pizza, quindi dividendo queste fette in due per ottenere l’interno e gruppi esterni”, ha detto Aron.

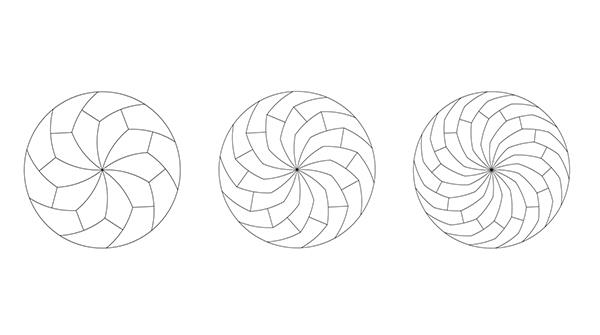
I due ricercatori si sono spinti ancora più in là, generalizzando la tecnica per avere a disposizione ancora più porzioni di pizza. Gli scienziati, in particolare, hanno mostrato che è possibile creare infinite tassellature anche con tessere aventi un numero dispari di lati. “Dal punto di vista matematico”, ha dichiarato Haddley al New Scientist, “non ci sono limiti”. A parte, naturalmente, la dimensione della pizza:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(Foto: Joel Haddley)

“Non so se la nostra ricerca avrà applicazioni che vanno al di là del taglio della pizza”, ha dichiarato il ricercatore. Ma i risultati sono “interessanti matematicamente, ed in grado di produrre qualche bella foto”.

In realtà, lo studio del taglio della pizza non è nuovo nelle discussioni matematiche. Infatti, come dichiarato da Gizmodo, “il taglio della pizza è un argomento molto studiato in matematica, principalmente perché ha poco a che fare con la pizza e più a che fare con la geometria circolare.”

 

[A cura di Alice Sepe]