Una nuova mini-serie, fatta di video e articoli, di Alessandro Zaccagnini, matematico, esperto di teoria dei numeri, autore del Dialogo sui numeri primi. Questa volta si fa accompagnare da una tartaruga per raccontarci cosa sono le somme esponenziali e perché sono tanto utili nella sua disciplina. Questa è la quinta e ultima puntata. Tutte le puntate le trovate su questa pagina.
Somme cubiche e oltre: fino ad arrivare là dove nessuna tartaruga è mai giunta prima!
=
\begin{cases}
\sqrt{p} & \text{se $p \equiv 1 \bmod 4$,} \\
\mathrm{i}\sqrt{p} & \text{se $p \equiv 3 \bmod 4$.}
\end{cases}\] Dunque il segno di una somma di Gauss è 1 nel primo caso, \(\mathrm{i}\) nel secondo. Dirichlet ha scoperto una formula simile per le somme nelle quali non c’è il vincolo che \(p\) sia un numero primo: abbiamo visto due disegni nella scorsa puntata. Il valore esatto di queste somme è completamente noto e non c’è molto da aggiungere a quanto abbiamo già detto.
La Congettura di Patterson riguarda monomi di terzo grado, cioè le somme cubiche del titolo, e piú precisamente la distribuzione del loro segno. Prendiamo un numero primo \(p\) e definiamo \[S(p)
=
\sum_{n = 0}^{p – 1} \mathrm{e}^{2 \pi \mathrm{i}n^3 / p}
=
1 + q + q^8 + q^{27} + q^{64} + \dots + q^{(p – 1)^3},\] dove \(q = \mathrm{e}^{2 \pi \mathrm{i}/ p}\). Qui \(f(n) = n^3 / p\) è il monomio di terzo grado che ci interessa.
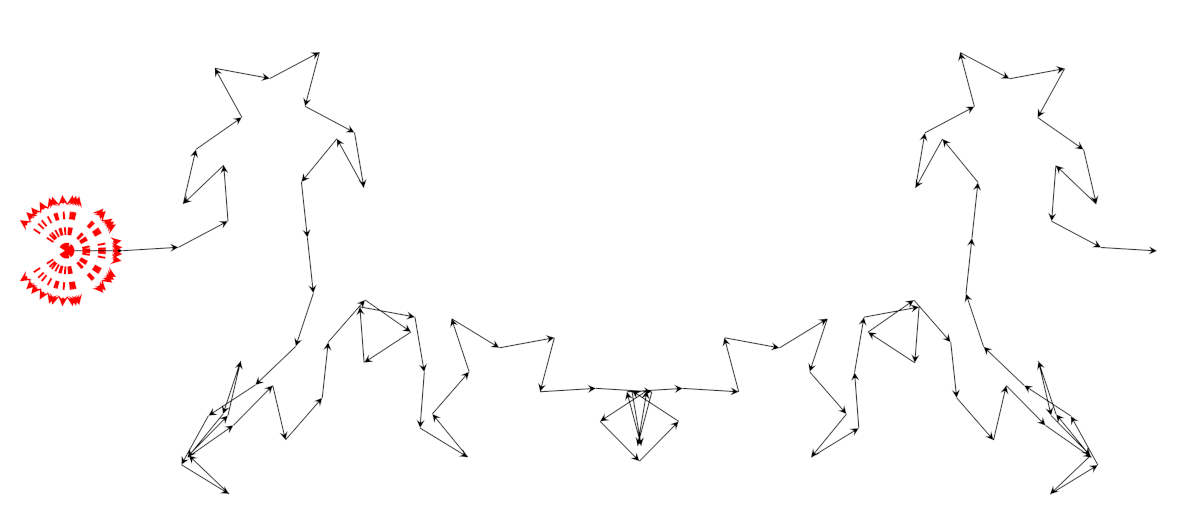
Vediamo qualche disegno prima di procedere, notando che c’è un caso che non compare quando trattiamo le somme quadratiche con i numeri primi: si tratta della figura a destra.
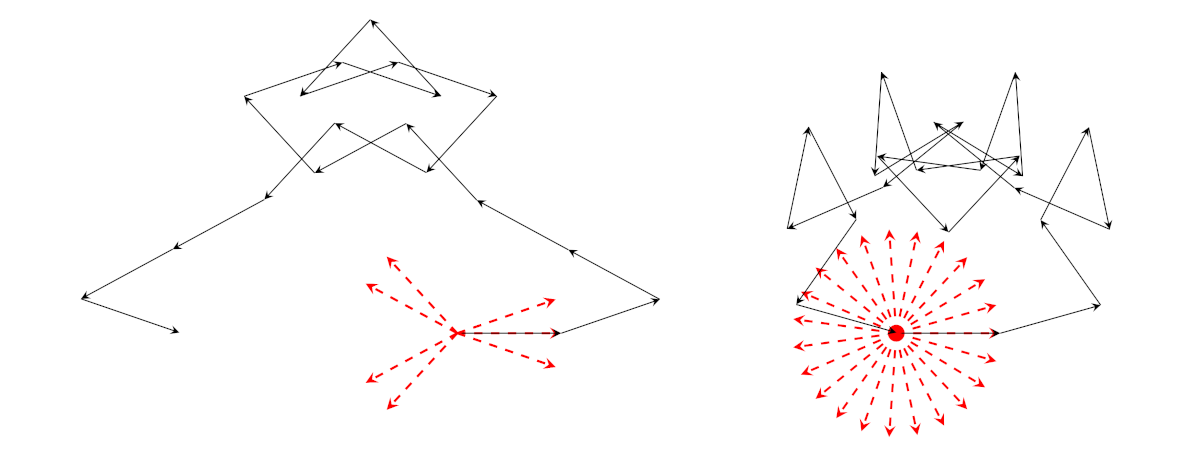
Somme cubiche per \(p = 19\) e \(p = 23\).
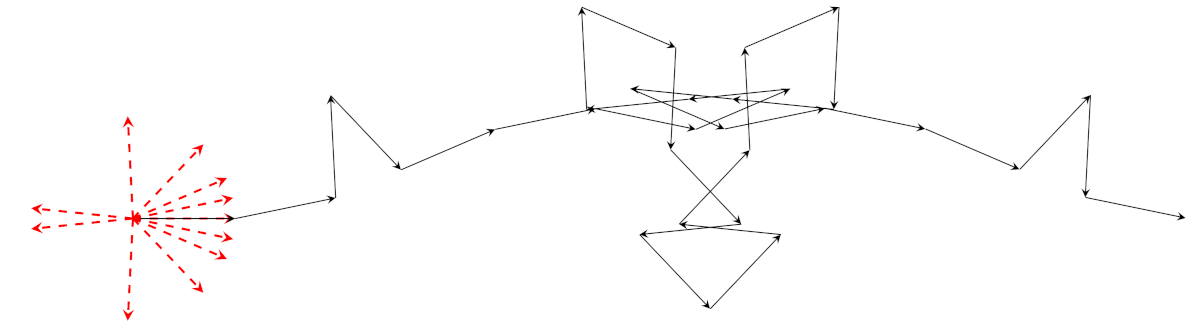
Somma cubica per \(p = 31\).
Queste figure mostrano comportamenti molto diversi fra loro: se \(p \equiv 1 \bmod 3\) (come nel caso \(p = 19\) oppure \(p = 31\)) allora i valori di \(x^3 \bmod p\) si concentrano in poche classi di resto modulo \(p\). Quindi la tartaruga tende a spostarsi molto dal punto di partenza nell’origine. In termini di equazioni, se \(n \in \mathbb{Z} / p \mathbb{Z} \setminus \{0\}\), allora l’equazione \(x^3 \equiv n \bmod p\) ha 0 o 3 soluzioni. Nella figura con \(p = 31\) ci sono solo 11 frecce rosse: una corrisponde al valore 0, le altre ai 10 cubi perfetti, ciascuno dei quali ha tre “radici cubiche.”
Se \(p \equiv 2 \bmod 3\) allora l’applicazione \(x \to x^3 \bmod p\) è una biiezione dell’insieme \(\mathbb{Z} / p \mathbb{Z}\) in sé. Questo tipo di biiezione è molto utile per le applicazioni alla crittografia (per esempio, nel crittosistema di Massey-Omura), ma dal nostro punto di vista è il caso meno interessante, perché ci riporta ai poligoni regolari, nei quali però prendiamo i vettori in un ordine diverso dal solito. Ricordiamo i disegni dei poligoni intrecciati della seconda puntata: anche in quella situazione abbiamo sommato gli stessi vettori che generano il poligono regolare in un ordine diverso; il percorso della tartaruga è piú o meno bizzarro come nella figura con \(p = 23\) qui sopra, ma alla fine deve tornare all’origine perché la somma di tutti i vettori vale 0. Anche nei numeri reali questa applicazione è una biiezione. In termini di equazioni, se \(n \in \mathbb{Z} / p \mathbb{Z}\), allora l’equazione \(x^3 \equiv n \bmod p\) ha esattamente una soluzione; in questo contesto, ogni elemento dell’insieme è un cubo perfetto, proprio come succede nei numeri reali.
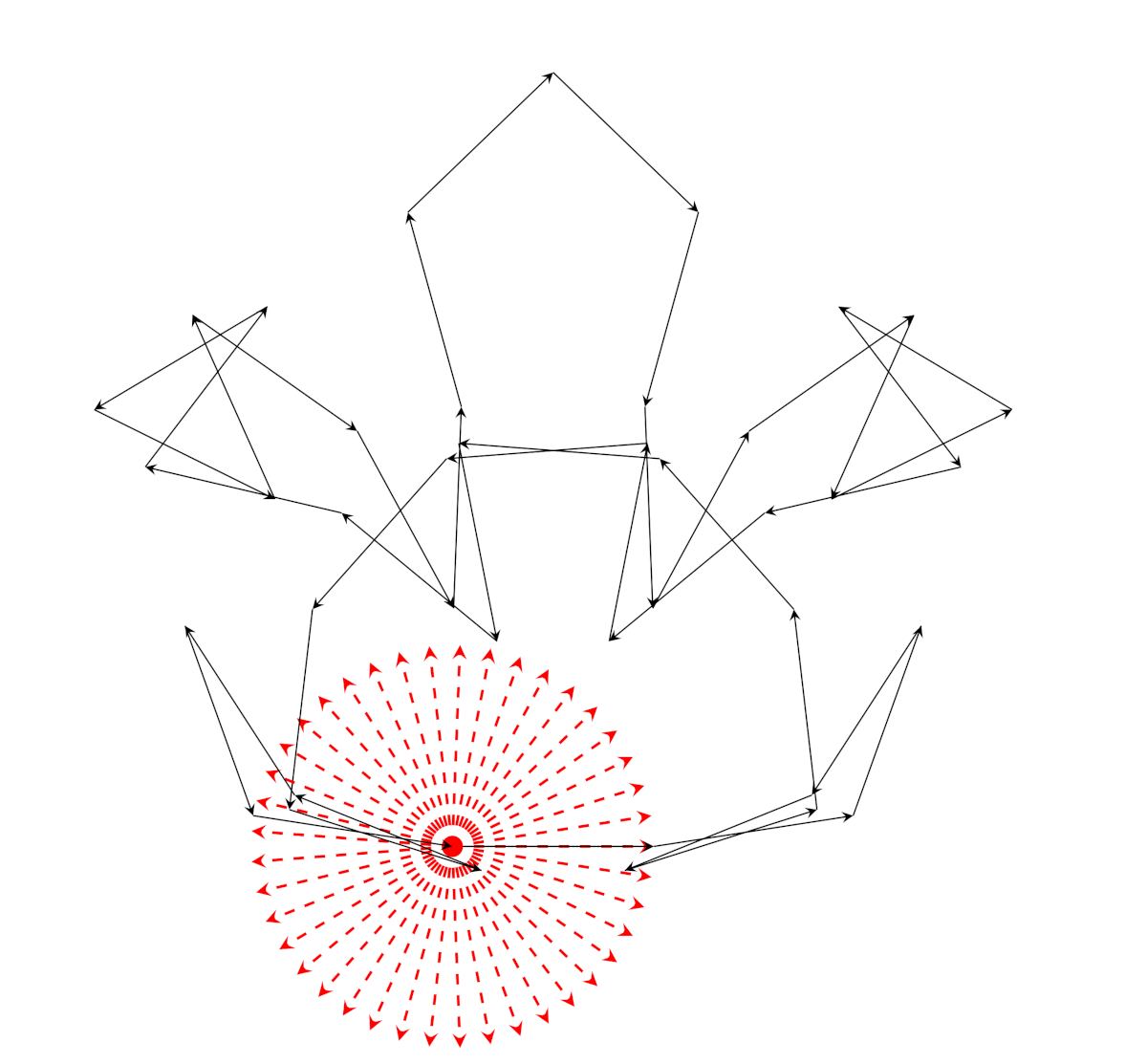
Possiamo finalmente svelare il mistero della figura data nell’introduzione della serie: si tratta della somma di Gauss cubica per \(p = 41\). L’applicazione \(x \mapsto x^3\) è una biiezione di \(\mathbb{Z} / 41 \mathbb{Z}\) in sé, come vediamo, e quindi la tartaruga torna all’origine disegnando una specie di immagine di sé stessa, per un bizzarro scherzo del caso.
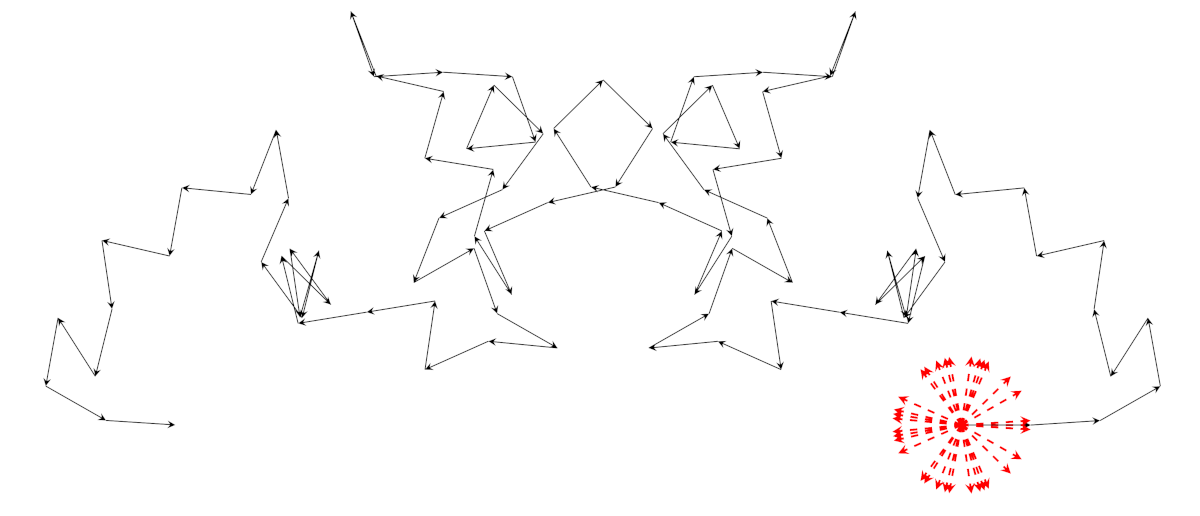
Invitiamo i lettori a provare altri valori, utilizzando la funzione data nella figura, o anche con altre funzioni. Qui sotto vediamo il grafico della somma cubica con \(p = 97\).
La Congettura di Patterson, dimostrata recentemente da Alexander Dunn & Maksym Radziwiłł [1 ]A. Dunn, & M. Radziwiłł, 2021. “Bias in Cubic Gauss Sums: Patterson’s Conjecture.” https://arxiv.org/abs/2109.07463., ha la sua origine in un problema posto da Ernst Kummer alla metà del XIX secolo. Kummer ha notato delle strane irregolarità nella distribuzione del “segno” delle somme di Gauss cubiche associate ai numeri primi \(p \equiv 1 \bmod 3\). In effetti, ha osservato che \(S(p)\) è un numero reale, perché gli addendi \(q^{n^3}\) e \(q^{(p – n)^3}\) sono complessi coniugati e quindi hanno parti immaginarie opposte; inoltre vale la disuguaglianza \(\vert S(p) \vert \le2 \sqrt{p}\). Kummer ha infine notato che i numeri reali \[\frac{S(p)}{2 \sqrt{p}}\] non erano uniformemente distribuiti nell’intervallo \([-1, 1]\), almeno sulla base dell’evidenza numerica, piuttosto scarsa in effetti, che poteva fornire all’epoca. A tal proposito ha formulato una congettura sulla loro distribuzione, che è stata però confutata da Roger Heath-Brown e Donald Patterson nel 1979. A sua volta, Patterson ha formulato una nuova e piú precisa congettura, che è stata dimostrata condizionalmente da Dunn & Radziwiłł nel 2021.
to sommagausscubica :p :lunghezza
clearscreen
home
showturtle
setcolor pick [black]
make "angolo 360 / :p
make "n 0
repeat :p [
setheading 90 - :angolo * :n * :n * :n
fd :lunghezza
wait 10
make "n :n + 1]
endFunzione in logo per le somme cubiche: rispetto alle somme quadratiche cambia solo un’istruzione. Il disegno della copertina si ottiene con il comando sommagausscubica 103 40.
Approfondimento: le somme esponenziali in generale
Nella Teoria dei Numeri si usano spesso somme finite della forma \[S_N
=
\sum_{n = 0}^N a_n \mathrm{e}^{2 \pi \mathrm{i}f(n)},\] dove \((a_n)\) indica una successione di numeri reali. Questo corrisponde a prendere vettori che non hanno necessariamente lunghezza costante, come nei nostri esempi. Se \[\sum_{n = 0}^{+\infty} \vert a_n \vert
<
+\infty,\] allora si può considerare anche la forma infinita \[S
=
\sum_{n = 0}^{+\infty} a_n \mathrm{e}^{2 \pi \mathrm{i}f(n)}.\] Questo grado di flessibilità in piú rende le somme esponenziali uno strumento molto versatile e adatto a numerosissime applicazioni. Le somme finite possono essere interpretate come polinomi trigonometrici, usando la formula di Eulero-de Moivre e separando parte reale e immaginaria; le somme infinite sono serie di Fourier. Derogando dalla richiesta di avere vettori di lunghezza unitaria o di avere somme finite otteniamo un livello ulteriore di adattabilità che rende le somme esponenziali tanto utili.
Le applicazioni delle somme esponenziali sono molto numerose: abbiamo accennato per esempio all’uniforme distribuzione delle successioni. Poi vale certamente la pena di ricordare la teoria fine della funzione zeta di Riemann e i problemi come quelli di Goldbach o di Waring; in generale tutti i problemi additivi che si possono affrontare con il metodo del cerchio, a cui ho accennato in un articolo su Ramanujan [2 ]A. Zaccagnini, 2020. “Cent’anni Senza Ramanujan.” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/langolo-arguto/senza-ramanujan/., nel quale si trasforma il problema aritmetico di “contare” il numero di soluzioni di qualche equazione in un integrale fatto sulla circonferenza unitaria di una funzione che è prodotto di opportune somme esponenziali.
È noto che Gauss si divertiva con le somme di radici dell’unità. Oltre ad aver studiato le somme che hanno preso il suo nome, ha scoperto un algoritmo per la moltiplicazione di interi basato su quella che oggi chiamiamo Trasformata di Fourier Discreta (riscoperto poi negli anni ’60 del XX secolo) che è ancora oggi uno dei migliori algoritmi noti per questo particolare problema, che si basa, per l’appunto, su alcune proprietà delle somme esponenziali tra cui quelle che abbiamo richiamato qui. Algoritmi efficienti per la moltiplicazione sono necessari nelle applicazioni in tempo reale, come la televisione ad alta definizione.
Le somme di Gauss quadratiche sono studiate in dettaglio nel Capitolo 2 del bellissimo libro di Harold Davenport [3 ]H. Davenport, 2000. Multiplicative Number Theory. Third. Vol. 74. Graduate Texts in Mathematics. Springer., uno dei migliori classici in circolazione. Le somme cubiche e il problema di Kummer, con alcune soluzioni parziali, sono descritti nel Capitolo 3.
Nelle applicazioni citate sopra è spesso indispensabile sapere quanto è grande la somma esponenziale in funzione del numero degli addendi. Uno degli strumenti utilizzati è il metodo della fase stazionaria, che abbiamo implicitamente utilizzato nella quarta puntata. Il metodo si basa su questa semplice osservazione: molti vettori consecutivi puntano nella stessa direzione se la derivata di \(f\) è vicina ad un intero, cioè se \(f\) (la fase) è vicina ad un suo punto stazionario modulo 1. Nell’esempio delle somme di Gauss abbiamo \(f(x) = x^2 / p\) con derivata \(f'(x) = 2 x / p\) che è vicina a 0 modulo 1 quando \(x\) è vicino ad un multiplo di \(p\) o di \(p / 2\), come abbiamo visto sopra quando abbiamo studiato i tratti pressoché orizzontali o verticali percorsi dalla tartaruga nelle somme di Gauss quadratiche. Se invece \(f’\) è vicina ad \(\frac12\) modulo 1 allora la tartaruga percorre un tratto a spirale perché vettori i consecutivi sono pressoché opposti e non si allontana molto dal punto in cui si trova per molti valori successivi.
Per certi versi, le somme esponenziali quadratiche si comportano per lunghi tratti come un cammino casuale. Da un certo punto di vista, rappresentano un cammino casuale ideale, in cui la distanza totale percorsa è pari alla radice quadrata del numero di passi fatti. Come ho ricordato nell’articolo sulla funzione di Möbius [4 ]A. Zaccagnini, 2021. “Una Passeggiata Aleatoria Ci Porterà Sulla Vetta Della Congettura Di Riemann?” Sito Web MaddMaths! https://maddmaths.simai.eu/ricerca/aleatoria-riemann/., dimostrare il risultato analogo per alcune somme esponenziali legate alla funzione zeta di Riemann porterebbe alla dimostrazione della famosa Congettura (vedi anche [5 ]A. Zaccagnini, 2016. “Una Versione Elementare Della Congettura Di Riemann.” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/una-versione-elementare-della-congettura-di-riemann/..
Conclusioni e ringraziamenti
Rileggendo un’ultima volta quello che ho scritto, mi accorgo che forse non sono riuscito a spiegare con precisione che cosa sono e a cosa servono le somme esponenziali, ma spero di essere riuscito a spiegare perché mi piace tanto la matematica e perché secondo me è cosí bella!
Un grande ringraziamento va a Roberto Natalini, per tutto il lavoro dietro le quinte e per aver insistito con me quel tanto che basta per farmi scrivere questa serie di articoli. Ringrazio anche Riccardo Fumagalli per aver creato la bellissima immagine della copertina di questa serie.
Note e riferimenti
| ⇧1 | A. Dunn, & M. Radziwiłł, 2021. “Bias in Cubic Gauss Sums: Patterson’s Conjecture.” https://arxiv.org/abs/2109.07463. |
|---|---|
| ⇧2 | A. Zaccagnini, 2020. “Cent’anni Senza Ramanujan.” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/langolo-arguto/senza-ramanujan/. |
| ⇧3 | H. Davenport, 2000. Multiplicative Number Theory. Third. Vol. 74. Graduate Texts in Mathematics. Springer. |
| ⇧4 | A. Zaccagnini, 2021. “Una Passeggiata Aleatoria Ci Porterà Sulla Vetta Della Congettura Di Riemann?” Sito Web MaddMaths! https://maddmaths.simai.eu/ricerca/aleatoria-riemann/. |
| ⇧5 | A. Zaccagnini, 2016. “Una Versione Elementare Della Congettura Di Riemann.” Sito Web MaddMaths! https://maddmaths.simai.eu/divulgazione/una-versione-elementare-della-congettura-di-riemann/. |