Una nuova mini-serie, fatta di video e articoli, di Alessandro Zaccagnini, matematico, esperto di teoria dei numeri, autore del Dialogo sui numeri primi. Questa volta si fa accompagnare da una tartaruga per raccontarci cosa sono le somme esponenziali e perché sono tanto utili nella sua disciplina. Questa è la quarta puntata. Tutte le puntate le trovate su questa pagina.

Somme di Gauss

La somma di Gauss quadratica con \(p = 101\)In questa puntata studieremo il caso, introdotto da Gauss, in cui \(f\) è un monomio di secondo grado e le cose cambieranno drasticamente. Prendiamo un numero primo \(p\) e definiamo \[S(p)
=
\sum_{n = 0}^{p – 1} \mathrm{e}^{2 \pi \mathrm{i}n^2 / p}
=
1 + q + q^4 + q^9 + q^{16} + \dots + q^{(p – 1)^2},\] dove \(q = \mathrm{e}^{2 \pi \mathrm{i}/ p}\). Qui \(f(n) = n^2 / p\) è il monomio di secondo grado che ci interessa.

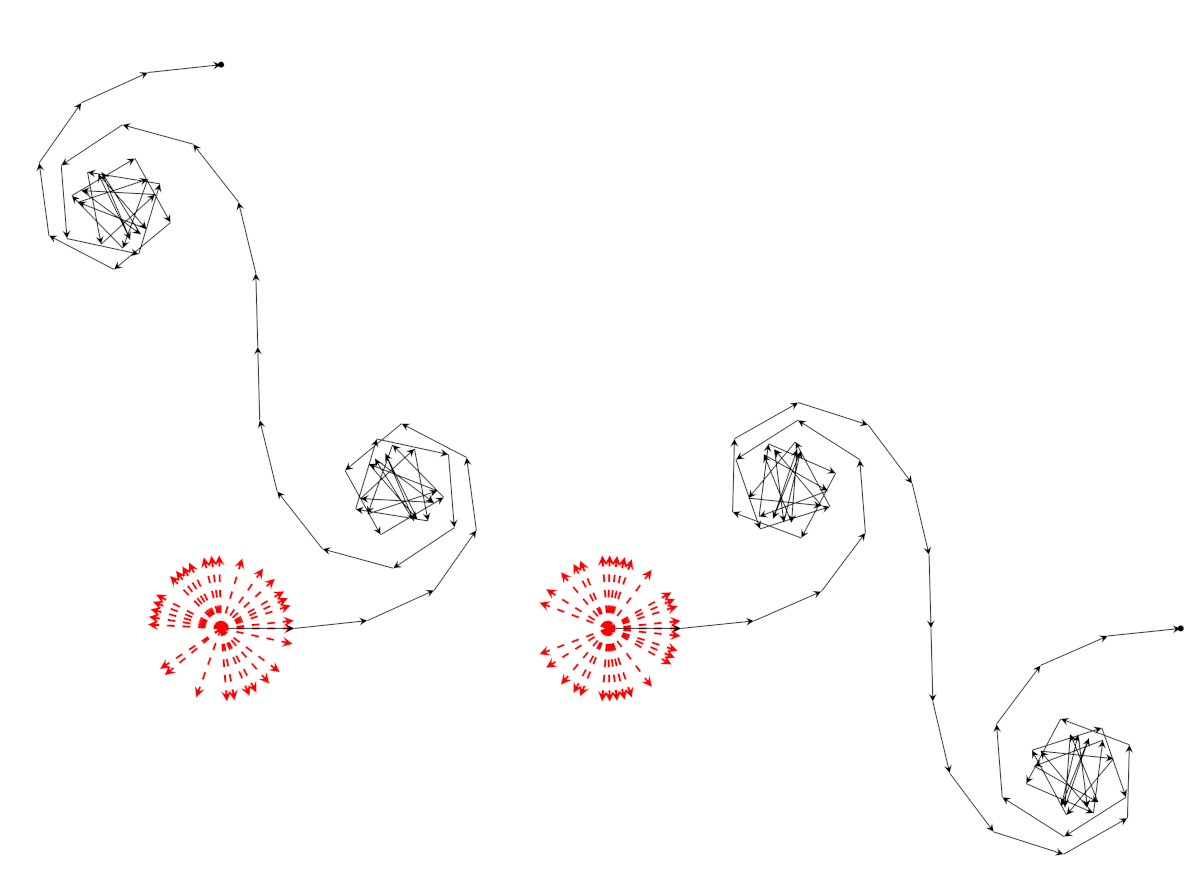
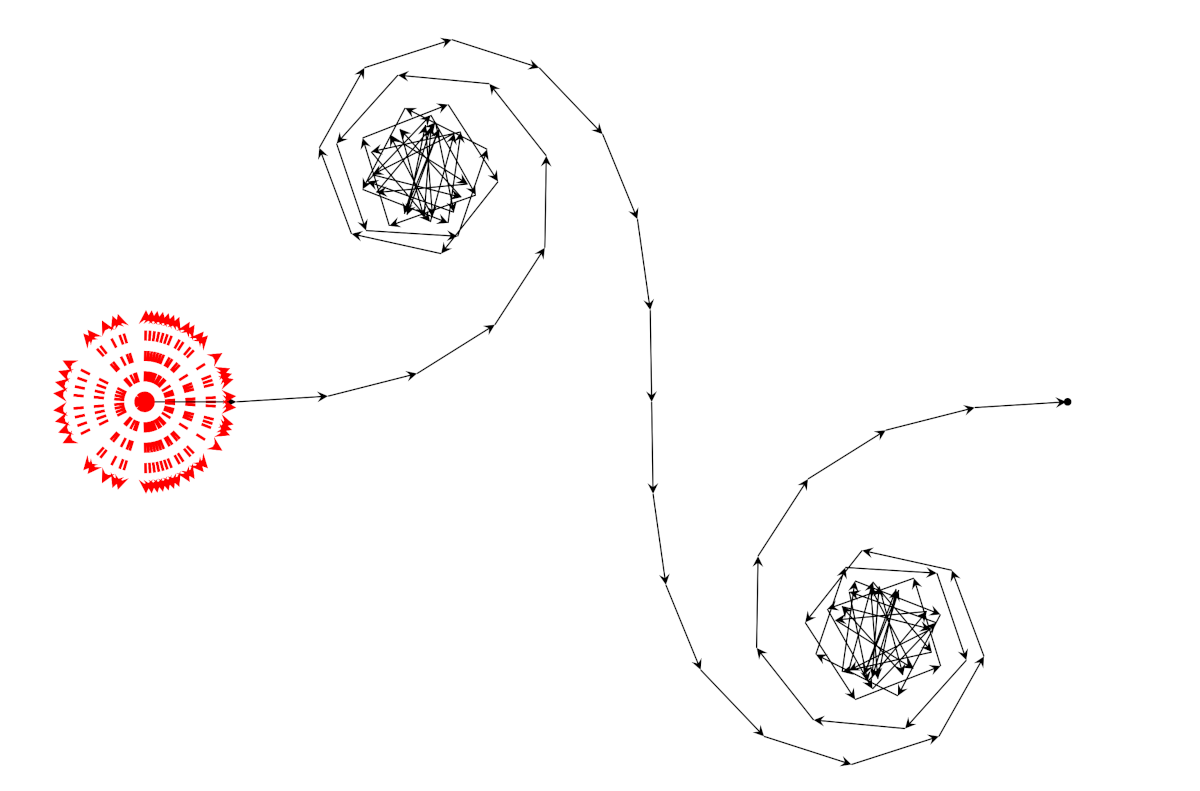
A sinistra la somma di Gauss \(S(59)\), a destra la somma di Gauss \(S(61)\).

Ci sono due casi con un comportamento diverso: \(p \equiv 1 \bmod 4\) e \(p \equiv 3 \bmod 4\); li vediamo illustrati nella figura qui sopra. Gauss stesso ha dimostrato che \(S(p) = \sqrt{p}\) nel primo caso (a destra nella figura) ed \(S(p) = \mathrm{i}\sqrt{p}\) nel secondo. In entrambi i casi, ogni tanto la tartaruga fa una sequenza di passi in direzione quasi orizzontale, ogni tanto fa una sequenza di passi piú o meno in verticale, ogni tanto fa vorticose piroette che la lasciano quasi nello stesso punto.

Notiamo che i quadrati perfetti “mancano” alcune direzioni, come si vede chiaramente dalla figura, esattamente come i quadrati perfetti dei numeri reali “mancano” tutti i numeri negativi. Se \(p \equiv 1 \bmod 4\), allora \(x\) è un quadrato perfetto se e solo se \(-x\) lo è; quindi la somma di Gauss è reale, perché le parti immaginarie dei vettori unitari si elidono. Si noti la simmetria dei vettori rossi rispetto all’asse reale. Se \(p \equiv 3 \bmod 4\), allora \(x\) è un quadrato perfetto se e solo se \(- x\) non lo è, e la somma di Gauss è immaginaria pura.

Notiamo che i primi e gli ultimi passi della tartaruga sono in entrambi i casi pressoché orizzontali, perché quando \(n\) è molto vicino a 0 oppure a \(p\) allora \(f(n) = n^2 / p\) è molto vicino ad un numero intero e quindi \(\mathrm{e}^{2 \pi \mathrm{i}f(n)}\) è molto vicino ad 1. Inoltre, i passi che la tartaruga compie in verticale vanno verso l’alto se \(p \equiv 3 \bmod 4\) e verso il basso se \(p \equiv 1 \bmod 4\). La direzione dipende dal fatto che se \(p = 4 k + 2 + \delta\) con \(\delta \in \{ \pm 1 \}\) allora \[\frac1p \Bigl( \frac{p – 1}2 \Bigr)^2
–
k
=
\frac14 \delta + \frac1{4 p}
\approx
\frac14 \delta.\] Questo significa che se \(n = \frac12 (p – 1)\) allora l’addendo della somma di Gauss corrispondente, cioè \(\mathrm{e}^{2 \pi \mathrm{i}f(n)}\), vale circa \(\mathrm{e}^{2 \pi \mathrm{i}/ 4} = \mathrm{i}\) se \(p \equiv 3 \bmod 4\) (quando \(\delta\) vale 1) e \(\mathrm{e}^{-2 \pi \mathrm{i}/ 4} = – \mathrm{i}\) se \(p \equiv 1 \bmod 4\) (quando \(\delta\) vale \(-1\)). Quando \(n\) è “lontano” da un multiplo di \(p\) o di \(\frac12 p\) allora i valori consecutivi di \(n^2\) sono “scorrelati” modulo \(p\) e per un breve tratto il moto della tartaruga somiglia ad un cammino casuale. Si tratta proprio delle spirali del titolo di questa serie.

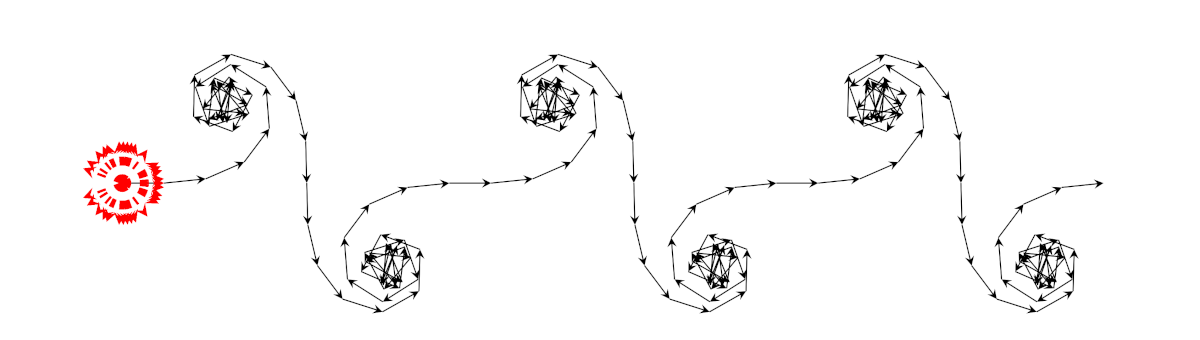
Disegniamo la somma di Gauss \(S(61)\), ma poi lasciamo la tartaruga libera di proseguire, sommando altri termini della somma esponenziale: la tartaruga si allontana verso \(+\infty\) perché \(61 \equiv 1 \bmod 4\). Si sposta verso infinito lungo l’asse immaginario se \(p \equiv 3 \bmod 4\).

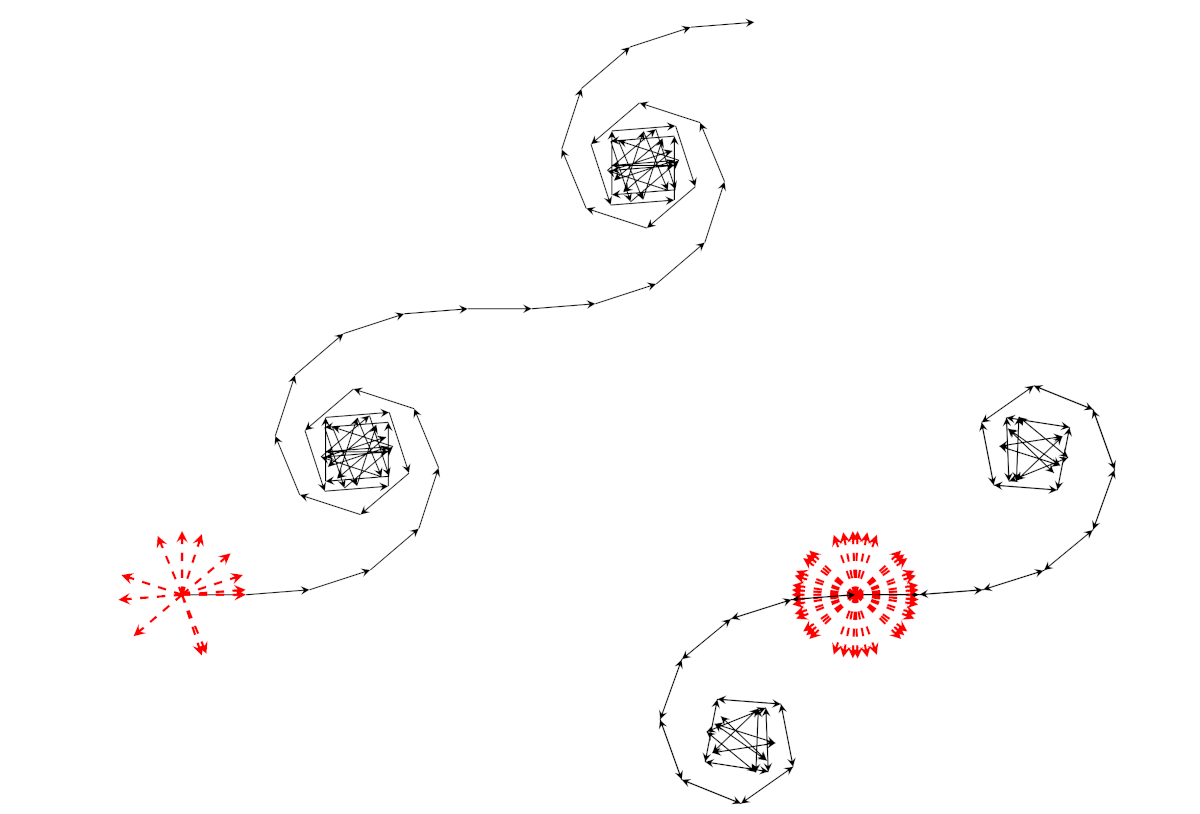
Somma di Gauss con \(p = 80\) e \(p = 82\). Dirichlet ha trovato una formula generale per calcolare il valore della somma di Gauss in cui \(p\) non è vincolato ad essere un numero primo. Nel secondo caso, la tartaruga percorre la mezza spirale in alto a destra, poi torna esattamente sui suoi passi fino all’origine, percorre la mezza spirale in basso a sinistra e ritorna al punto di partenza.

to sommagauss :p :lunghezza
  clearscreen
  home
  showturtle
  setcolor pick [black]
  make "angolo 360 / :p
  make "n 0
  repeat :p [
    setheading 90 - :angolo * :n * :n
    fd :lunghezza
    wait 10
    make "n :n + 1]
end

Una funzione in logo per disegnare la somma di Gauss per un numero intero \(p\). Nella prima istruzione del ciclo scriviamo esplicitamente la direzione in cui deve puntare la tartaruga come funzione della variabile :n, tenendo conto del fatto che la direzione 0 corrisponde a \(90^\circ\) e che vogliamo ruotare in senso antiorario. Il disegno della copertina si ottiene dando il comando sommagauss 101 40.