Una nuova mini-serie, fatta di video e articoli, di Alessandro Zaccagnini, matematico, esperto di teoria dei numeri, autore del Dialogo sui numeri primi. Questa volta si fa accompagnare da una tartaruga per raccontarci cosa sono le somme esponenziali e perché sono tanto utili nella sua disciplina. Questa è la seconda puntata. Tutte le puntate le trovate su questa pagina.

Un po’ di calcoli

Pentagono regolare e pentagono intrecciatoLe figure viste nella prima puntata sembrano indicare che se ruotiamo il vettore di partenza di $(360 / n)^\circ$ e sommiamo i vettori ottenuti via via, dopo esattamente $n$ passi torniamo all’origine, dopo aver descritto un $n$-agono regolare, per ogni intero $n \ge 3$. È veramente cosí? E se sí, perché? Se proviamo a fare il contrario, cioè partiamo dal poligono regolare e otteniamo i corrispondenti vettori unitari, è chiaro che questi formano angoli costanti fra ciascuno e il successivo.

Per giustificare questa scoperta empirica e dimostrarla in generale abbiamo bisogno di utilizzare i numeri complessi. In particolare, ci serve ricordare le forma esponenziale dei numeri complessi e la proprietà che moltiplicare corrisponde a sommare la fase. Se $z_1$ e $z_2$ sono numeri complessi, esistono numeri reali $\rho_1 \ge 0$ e $\rho_2 \ge 0$, e $\theta_1$, $\theta_2 \in [0, 2 \pi)$ tali che $$z_1 = \rho_1 \mathrm{e}^{\mathrm{i}\theta_1} \qquad\text{e}\qquad z_2 = \rho_2 \mathrm{e}^{\mathrm{i}\theta_2} \qquad\text{e dunque}\qquad z_1 z_2 = \rho_1 \rho_2 \mathrm{e}^{\mathrm{i}(\theta_1 + \theta_2)}.$$ Tutti i nostri vettori sono unitari, cioè hanno $\rho = 1$ e quindi ci dobbiamo preoccupare solo delle fasi, cioè dei numeri $\theta$, che rappresentano gli angoli di cui stiamo parlando.

Per $n \ge 3$ poniamo $\alpha_n = 2 \pi / n$; dunque $\alpha_n$ è un $n$-esimo di un angolo giro, misurato in radianti. La rotazione di $\alpha_n$ corrisponde alla moltiplicazione per $q = q_n = \mathrm{e}^{\mathrm{i}\alpha_n}$. I vettori che consideriamo sono dunque $$1, q, q^2, q^3 , \dots, q^{n – 1}.$$ Questi numeri complessi sono detti radici $n$-esime dell’unità, perché sono tutte e solo le soluzioni complesse dell’equazione $z^n = 1$; sono i punti che si trovano in corrispondenza delle punte delle frecce rosse nelle figure della prima puntata.

Per calcolare il valore di $S(q) = 1 + q + q^2 + \dots + q^{n – 1}$ abbiamo bisogno di ricordare la formula per la somma dei primi termini di una progressione geometrica: se $x$ è un qualunque numero complesso diverso da 1 ed $m \ge 0$ è intero, allora $$%\label{sum-prog} 1 + x + x^2 + \dots + x^m = \frac{1 – x^{m + 1}}{1 – x}.$$ La dimostrazione di questa formula, che era certamente nota agli antichi Greci, si ottiene facilmente per induzione. Nel caso che ci interessa abbiamo $x = q$ ed $m = n – 1$: sostituendo nella formula qui sopra e ricordando che $q^n = 1$ troviamo che effettivamente $S(q) = 0$. In alternativa, $S(q) = 1 + q + q^2 + \dots + q^{n – 1} = q^n + q + q^2 + \dots + q^{n – 1} = q + q^2 + \dots + q^{n – 1} + q^n = q S(q)$, cioè $(q – 1) S(q) = 0$; poiché $q \ne 1$ concludiamo che $S(q) = 0$. In effetti, $q S(q)$ non è altro che la somma degli stessi vettori cominciando dal secondo e finendo con il primo.

La successione $1, q, q^2, q^3, \dots$, prolungata oltre i primi $n$ valori, è periodica di periodo $n$, proprio perché $q^n = 1$, e quindi si ripete da capo. Dunque, se invece di sommare $n$ termini consecutivi ne sommiamo $2 n$, o $3 n$ o un qualunque multiplo di $n$ troviamo 0: la tartaruga ritorna esattamente sui suoi passi e ripete lo stesso percorso in eterno. Questo dipende dal fatto che l’angolo di cui ruotiamo è un sottomultiplo di un angolo giro; lo stesso succede, piú in generale, se l’angolo è in rapporto razionale con l’angolo giro. Questo è il caso illustrato nella prossima figura, nella quale abbiamo un poligono “intrecciato.”

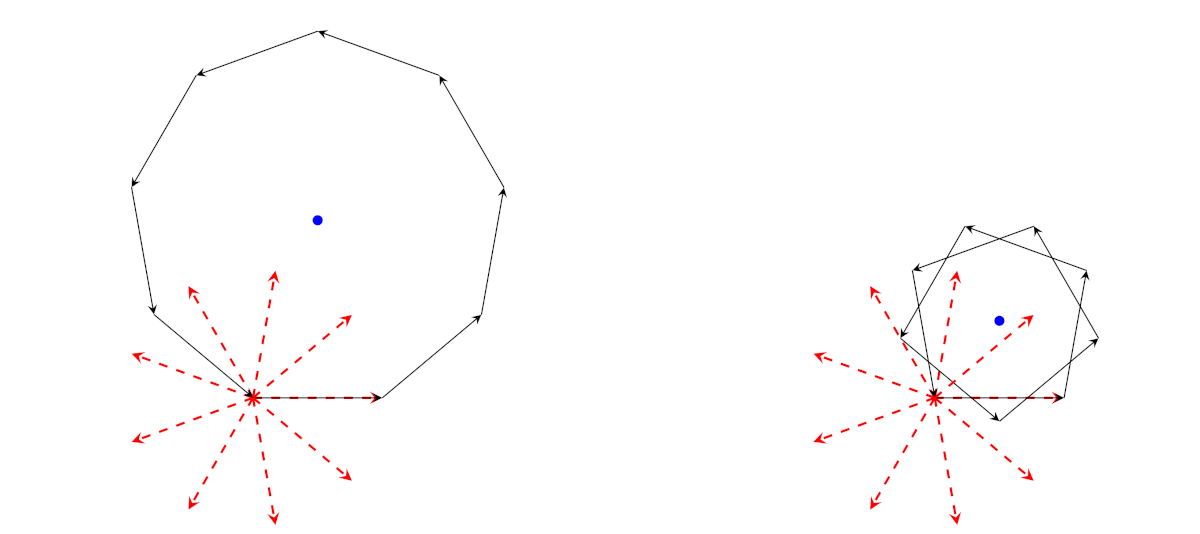
A sinistra il caso $n = 9$; a destra prendiamo gli stessi vettori in un altro ordine. Invece di ruotare di $40^\circ = (360 / 9)^\circ$ ruotiamo di $80^\circ$. La somma di tutti i vettori, evidentemente, ha lo stesso valori di prima e cioè 0, ma invece di ottenere il poligono regolare otteniamo un poligono intrecciato.

to poligono :lunghezza :angolo :iterazioni
  clearscreen
  showturtle
  setheading 90
  pendown
  setcolor pick [red]
  repeat :iterazioni [
    fd :lunghezza
    setxy 0 0
    rt -:angolo
    wait 10]
  penup
  home
  pendown
  setheading 90
  setcolor pick [black]
  repeat :iterazioni [
    fd :lunghezza
    rt -:angolo
    wait 10]
end

Una funzione in logo per generare una sequenza di :iterazioni vettori di lunghezza :lunghezza, ciascuno ruotato di :angolo gradi in direzione antioraria rispetto al precedente, ed il “poligono” associato. Qui l’angolo di rotazione è specificato esplicitamente e non calcolato a partire dagli altri dati: il “poligono” che si ottiene potrebbe non chiudersi, come negli esempi che seguiranno, e quindi è necessario indicare il numero di iterazioni desiderate. L’istruzione poligono 200 80 9 richiama la funzione e disegna il poligono intrecciato della figura precedente.