La sensazione di colore è frutto di una lunga evoluzione e la sua modellizzazione matematica, completa o parziale, rimane ancora un problema aperto. Edoardo Provenzi, professore all’Université de Bordeaux, ci guida in un sorprendente percorso, lungo più di tre secoli, ricostruendo le tappe fondamentali dello studio matematico del colore, terminando con un racconto del suo particolare cammino scientifico. Le puntate precedenti le trovate qui: prima puntata, seconda puntata.

Nell’articolo precedente abbiamo cominciato a vedere come due tra i più grandi scienziati di tutti i tempi, Newton e Maxwell, abbiano fondato le basi sia matematiche che sperimentali per lo studio del colore. In questo articolo  vedremo come le loro idee siano state portate avanti attraverso un percorso cronologico da altri eminenti studiosi.

Young: “il visionario”

Thomas Young, 1773-18, inglese, fu un uomo molto eclettico, si annoverano infatti suoi contributi nel campo della fisica, della fisiologia, della linguistica e perfino dell’egittologia. Il suo più importante apporto alla teoria del colore è l’ipotesi che la possibilità di ricostruire colori a partire da soli tre luci opportunamente scelte non sia una proprietà fisica della luce, ma una proprietà biologica dei nostri occhi. Young si spinse a dire, senza alcuna base fisiologica, che nei nostri occhi esistono fibre nervose con tre porzioni separate che rispondono in modo differente alla luce, per questa ragione la sua ipotesi passò alla storia come la teoria tricromatica del colore. Come si comprese successivamente, questa ipotesi è solo parzialmente corretta: oggi sappiamo che nella retina dei nostri occhi esistono tre fotorecettori con sensibilità diverse alla luce, chiamati “coni” a cause della loro forma. I coni hanno la capacità di assorbire la luce, ciò crea una differenza di potenziale elettrico della loro membrana che, a sua volta, produce una scarica di corrente elettrica che si propaga alle fasi successive della catena visuale. Nella figura seguente sono mostrate le cosiddette “curve di sensibilità” dei coni.

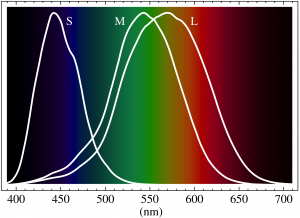Queste curve rappresentano la probabilità che un’onda elettromagnetica che oscilla con una certa lunghezza d’onda sia assorbita da un cono e, come si vede, i tre tipi di coni diversi massimizzano questa probabilità in tre punti differenti dello spettro luminoso: la zona del blu per i coni detti “S”, quella del verde per i coni detti “M” e quella gialla per i coni detti “L”, la ragione di questi simboli deriva dall’inglese “short”,  “medium” e “long”, ovvero corta, media e lunga, in riferimento alla lunghezza d’onda corrispondente.  Comunemente, ma sbagliando, questi coni vengono detti, rispettivamente, del blu, verde e rosso, l’errore è ovviamente dovuto al fatto che il picco di probabilità d’assorbimento dei coni L non è nella regione del rosso spettrale, ma in quella del giallo spettrale, come detto in precedenza.  La discrepanza tra l’idea di Young e l’evidenza fisiologica dei coni non toglie nulla al carattere visionario della sua ipotesi, difatti Young è riconosciuto come il primo scienziato a formulare una teoria compiuta nella quale si ipotizza che il colore non derivi solo da fenomeni fisici esterni agli esseri umani, ma anche da fenomeni biologici interni. 

Von Helmholtz: “il formalizzatore” 

Hermann von Helmoltz, 1821-1894  fisico-matematico e medico tedesco. Nel 1851 riscatta dall’oblio l’ipotesi tricromatica di Young, che non fu presa molto sul serio dai suoi coevi, e ne fa un utilizzo innovativo all’interno di una teoria matematicamente rigorosa, tanto che oggi si parla della teoria tricromatica di Young-Helmholtz.  È inoltre notevole un suo lavoro del 1891 nel quale propone il primo studio formale per definire una “distanza percettiva tra colori”, utilizzando i cosiddetti “elementi di linea”, un concetto fondamentale della (poco più che) neonata geometria differenziale, ben conosciuta tra i matematici tedeschi nella seconda metà del 1800 grazie all’influenza del “principe dei matematici” Gauss e del suo altrettanto geniale allievo Riemann.  Riguardo a quest’ultimo, non si può non citare il gustosissimo aneddoto che riguarda la sua memorabile dissertazione per l’abilitazione a professore del 1854: su richiesta di Gauss, Riemann preparò una memoria nella quale poneva le basi per quello che sarebbe diventato il concetto di varietà differenziabile astratta, ovvero il fondamento della geometria differenziale moderna. 

Riemann citò solo due esempi “pratici” di varietà differenziabile, curiosamente, legandoli entrambi…alla percezione! Sostenne infatti che lo spazio percepito e i colori percepiti fossero due varietà differenziabili! Rimane ancora un mistero cosa lo portò a questa intuizione, ma, come spesso accade ai geni, Riemann ci aveva visto lungo, molto lungo…

Grassmann: “l’algebrista del colore” 

Hermann Günther Grassmann, 1809-1877, matematico, linguista e…tuttologo tedesco. Animato da una fame di sapere insaziabile, Grassmann si occupò di un po’ tutti i campi del sapere. Tra i matematici è noto, tra l’altro, per aver posto le basi per la formalizzazione dell’importantissima e onnipresente algebra lineare. È proprio cercando un esempio pratico per l’applicazione del concetto di “combinazione lineare” che operò dei famosi test di percezione visiva e, nel 1853, pubblicò quelle che oggi sono note come le “leggi di Grassmann” le quali dicono, tra l’altro, che una “combinazione convessa di due colori è ancora un colore”, ovvero, detto in termini geometrici, che dati due colori qualunque, lo spazio che li contiene deve contenere anche il segmento di retta che li congiunge. In matematica si dice che uno spazio con questa proprietà è “convesso”. 

Schrödinger: “l’ordine nel caos”

Erwin Schrödinger, 1887-1961, fisico teorico austriaco. Più conosciuto per lavori di meccanica quantistica, nel 1920 pubblicò una serie di bellissimi articoli sul colore, operando una elegante fusione teorica dei risultati precedenti, simile, nello spirito, alle equazioni di Maxwell. È l’apice dello studio teorico sul colore della prima parte del ventesimo secolo. Schrödinger ha la profondissima intuizione che il colore può essere studiato non tanto come il risultato dell’interazione tra luce, occhi e cervello, ma attraverso le sue proprietà matematiche, essenzialmente algebriche, derivanti da osservazioni visuali.  Infatti, grazie a Grassmann, sappiamo che lo spazio (o, nei termini di Riemann, la varietà astratta) che contiene i colori percepibili dagli esseri umani dev’essere convesso, mentre già in Opticks di Newton si può evincere che questo spazio è un “cono”, un concetto che, in matematica, rappresenta il fatto che i multipli positivi di elementi di un insieme sono ancora elementi di quell’insieme. Nel caso di un colore, un multiplo positivo è da interpretare come un colore più “intenso”.  Schrödinger aggiunge un’osservazione sulla cosiddetta “regolarità” di questo cono, nel senso che esiste un vertice dato dal nero. Infine, la teoria tricromatica impone che il cono dei colori percepibili sia di dimensione 3. Schrödinger fuse tutte queste informazioni e le pose a fondamento di una teoria assiomatica del colore, sostenendo che lo spazio dei colori percepiti fosse un cono convesso regolare di dimensione 3.  Se qualche lettore può storcere il naso di fronte a questa astrazione, considerandola inutile o, peggio, inutilmente complicata, si ricordi quanto detto da Wigner o l’utilità delle equazioni differenziali di Maxwell per formalizzare e capire l’elettromagnetismo.  Quasi sempre, un lavoro di formalizzazione matematica, apparentemente astruso e incomprensibile all’inizio, si rivela essere una miniera d’oro dalla quale attingere gli strumenti per elucidare uno ad uno gli aspetti più reconditi di un problema o un fenomeno naturale. Vedremo successivamente quanto importanti siano gli assiomi di Schrödinger per la comprensione del colore.

Hering: “l’incompreso”

Ewald Hering, 1834-1918, fisiologo tedesco. Nel 1892, ispirato dai lavori di Schopenhauer, propose una teoria del colore alternativa a quella tricromatica. Partendo dal presupposto che il bianco è l’opposto del nero e che nessuno percepisce mai un rosso “verdastro” o un giallo “bluastro”, propose che un colore percepito sia caratterizzato, invece che da tre valori di rosso verde e blu, dal bilancio tra tre opposizioni: bianco e nero, rosso e verde, giallo e blu. Per questa ragione, la teoria di Hering è passata alla storia come la “teoria dei colori opponenti”. Il modello di Hering inizialmente fu più apprezzato in ambito umanistico che scientifico. Gli scienziati del colore, infatti, vedevano nella formalizzazione di von Helmholtz della teoria tricromatica inizialmente proposta da Young un modello solido e semplice allo stesso tempo. Per di più, non si capiva come, nella visione umana, si potessero conciliare queste due teorie. Oggi invece sappiamo che né la teoria tricromatica, né quella dei colori opponenti sono esaustive, tuttavia sono compatibili in quanto entrambe rappresentano uno stadio della complicatissima catena di eventi neurofisiologici che porta alla percezione del colore.  La base fisiologica della teoria di Hering è costituita dall’azione delle cellule retiniche che elaborano le correnti elettriche in uscita dai coni. In particolare, le cosiddette cellule gangliari “mescolano” i segnali arrivati dai coni in un modo coerente con quanto osservato da Hering. Possiamo quindi dire che la tricromia di Young e Helmholtz dà una modellizzazione matematica della prima fase della visione a colori, quella inerente ai coni, e che il modello a colori opponenti di Hering descrive la fase successiva, che possiamo ascrivere, facendo un’innocua semplificazione, alle cellule gangliari.  Come detto sopra, queste due fasi non sono sufficienti per spiegare tutti i fenomeni percettivi collegati al colore, in quanto le cellule gangliari passano le loro informazioni “opponenti” al nervo ottico e da qui compiono il loro lungo cammino verso il cervello per la loro elaborazione finale, nella zona chiamata V4 della corteccia occipitale. Occorre dire chiaramente che siamo ben lontani dal capire come il cervello compie questa elaborazione.

Edoardo Provenzi

#Fine terza parte

Barbara Nelli