Il modello di Malthus e l’equazione logistica sono i più noti modelli di crescita di popolazione. Tuttavia, ce n’è un altro, forse meno noto, ma particolarmente usato in biologia: il modello di Gompertz. Ce ne parla Marco Menale.
I modelli di crescita di popolazioni hanno una storia piuttosto lunga. Basti pensare ai conigli di Leonardo Fibonacci, già nel medioevo. Con l’età moderna si è avuta un’accelerata, grazie a nuovi strumenti matematici, come il calcolo differenziale. Tuttavia, quando si pensa a questi modelli ne vengono in mente due, i più noti: il modello malthusiano e l’equazione logistica. Il primo, dovuto all’inglese Thomas Robert Malthus, modella la crescita di una popolazione senza tener conto, tra gli altri, delle risorse limitate. Il secondo, sviluppato dal belga Pierre François Verhulst, assume un limite di sostenibilità ambientale. Eppure, ce n’è un terzo, meno noto, che, in un certo senso, si inserisce tra i due precedenti: il modello di Gompertz.
Benjamin Gompertz è stato un matematico britannico. Sebbene diversi premi matematici sin da giovane, non frequentò mai gli studi universitari per motivi di religione. Formatosi da autodidatta, si dedicò principalmente alla finanza, per poi finire a lavorare nelle compagnie assicurative. In questo contesto Gompertz scrisse il modello che porta ora il suo nome. E lo fece quantificando l’aspettativa di vita di una persona nella valutazione delle sua polizza assicurativa.
Per scrivere e comprendere questo modello, con la relativa equazione, partiamo da un problema reale. Vogliamo quantificare la crescita delle cellule tumorali in un tessuto. Sia \(N(0)\) il numero di queste cellule alla prima osservazione, \(t=0\). Sia \(r\) il tasso di crescita. Usando il modello di Malthus, l’evoluzione del numero di cellule segue l’equazione differenziale
\[N’(t)=rN(t).\]
Quindi, con semplici calcoli si arriva alla soluzione
\[N(t)=N(0)e^{r t}.\]
La crescita è esponenziale. E se questo comportamento è realistico nei primi istanti, non lo è su tempi lunghi. Infatti, spazio e nutrienti a disposizione delle cellule tumorali sono limitati. E poi c’è il fatto che un tumore forma tessuti necrotizzati che rallentano ulteriormente la crescita.
Ripartiamo dal modello malthusiano. Serve inserire un qualche fattore che modelli il rallentamento della crescita della popolazione tumorale. Lo si può modificare così:
\[ N’(t)=\left(\frac{r}{e^{a t}}\right)\,N(t).\]
Il fattore al denominatore, \( e^{a t}\), con \(a\) costante positiva, esprime il rallentamento della crescita. La soluzione di quest’equazione è
\[N(t)=N(0)\,e^\left({\displaystyle\frac{r}{a}-\displaystyle\frac{e^{-at}r}{a}}\right).\]
Una funzione di questo tipo è detta “gompertziana”. Come si vede dalla Figura 1, nella fase iniziale la crescita è molto rapida, quindi una sorta di malthusiana, ossia esponenziale. Mentre, dopo un certo tempo, quando le risorse a disposizione si riducono, così come lo spazio circostante, la crescita della popolazione rallenta, infatti la curva si schiaccia.
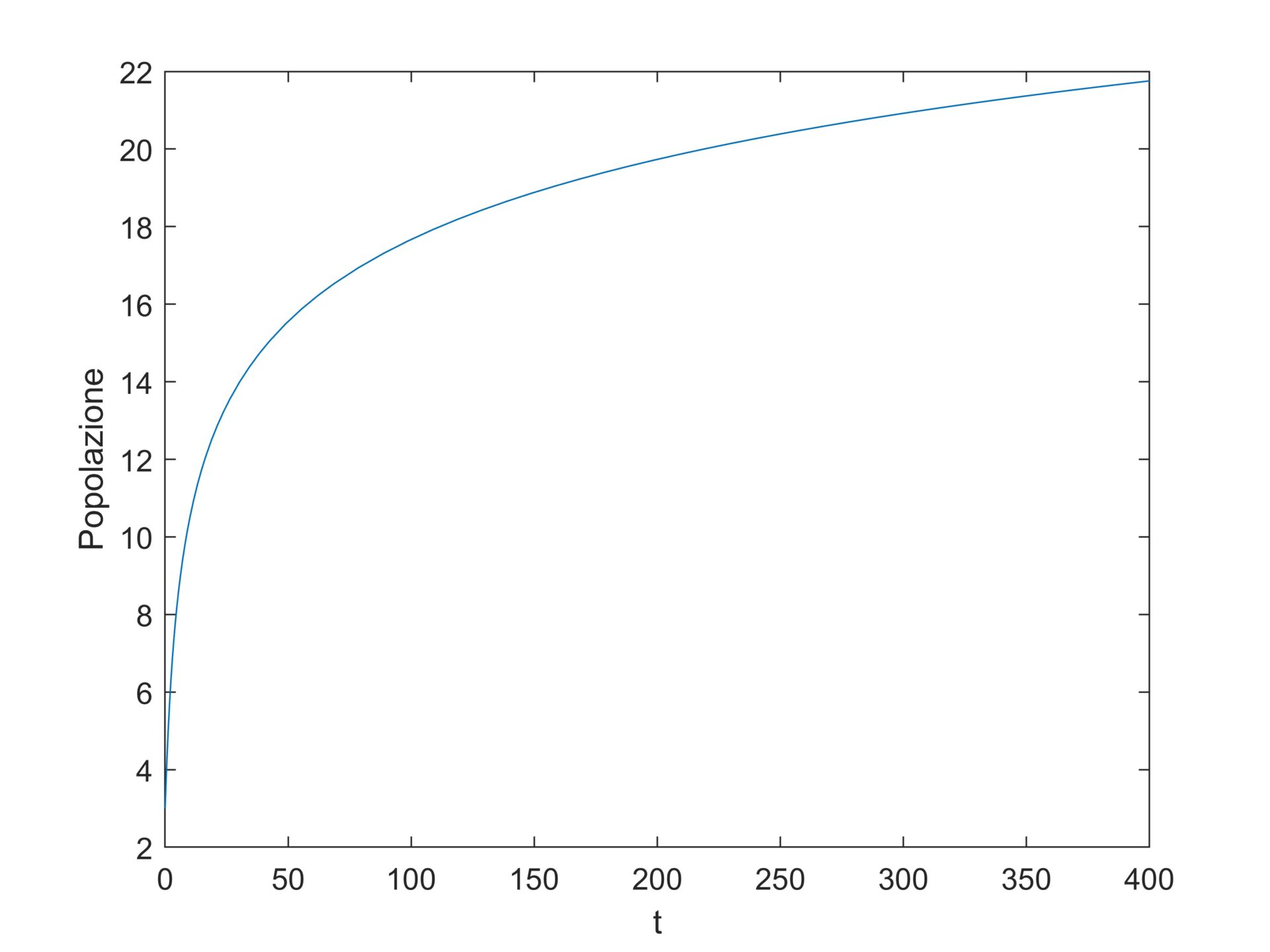
Figura 1. La curva di Gompertz.
Nota la massima capacità dell’ambiente, \(K\), ossia la popolazione massima che l’ambiente può sostenere, la legge di Gompertz si scrive come
\[N’(t)=-rN(t)\ln\left(\frac{N(t)}{K}\right).\]
Nella forma è simile alla logistica; infatti, quest’ultima è
\[N’(t)=rN(t)\left(1-\frac{N(t)}{K}\right).\]
Tuttavia, la curva di Gompertz conserva la rapida crescita iniziale, come una malthusiana, per poi schiacciarsi al valore limite \(K\), come la logistica (Figura 2). Ecco perché diciamo che si colloca tra i due.
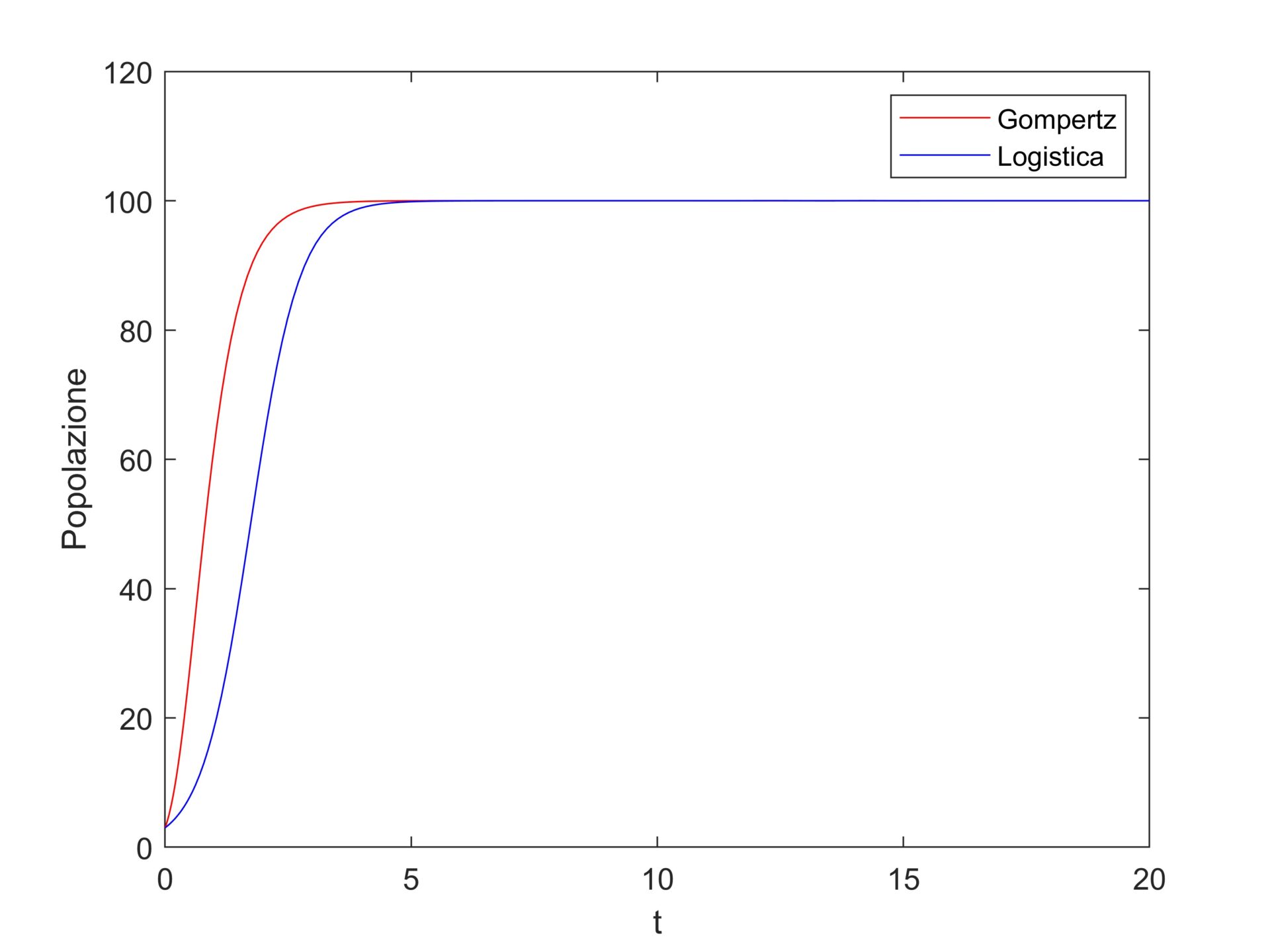
Figura 2. Confronto tra curva di Gompertz e curva logistica a parità di parametri.
Sebbene meno noto, il modello di Gompertz, anche in forme più complicate, è ampiamente diffuso in biologia. Infatti, lo si usa per lo studio e l’evoluzione delle neoplasie solide. Inoltre, trova applicazione per la crescita di popolazioni di animali, piante e batteri.























