Siamo quotidianamente sommersi dai dati. L’andamento e l’efficacia della campagna vaccinale, l’analisi dei risultati dopo il voto alle amministrative, la media goal di un attaccante di Serie A, per citarne alcuni. Eppure analisi diverse portano a considerazioni diverse. Nel caso del vaccino arriva la critica “dai dati emerge che in alcuni contesti ospedalizzazioni e ricoveri riguardano soprattutto i vaccinati”. Siamo nella situazione del Paradosso di Simpson.
Come in altri casi, la paternità del paradosso è dibattuta. Il primo ad occuparsene è lo statistico britannico George Udny Yule nell’articolo “Notes on the Theory of Association ” del 1903. Tuttavia il nome lo si deve allo statistico e crittoanalista britannico Edward Hugh Simpson con l’articolo del 1952 “The Interpretation of Interaction in Contingency Tables”. Cosa dice il paradosso? I risultati che emergono dai dati divisi in diversi gruppi possono invertirsi o scomparire se quei dati sono combinati.
Facciamo un esempio. Siamo i proprietari di un ristorante e vogliamo capire quale i clienti preferiscano tra peperoncino e pepe. Per fare questo, prepariamo uno stesso piatto, una volta condito con il peperoncino ed una seconda con il pepe. Un primo gruppo di 100 persone assaggia il piatto a base di peperoncino e di questi 80 lo apprezzano. Sono in 75 ad apprezzare il piatto condito con il pepe in un secondo gruppo di altre 100 persone. Il peperoncino piace dell’80% dei casi, mentre il pepe nel 75%. Sceglieremo così la prima soluzione.
Dividiamo ora i dati in base al sesso.
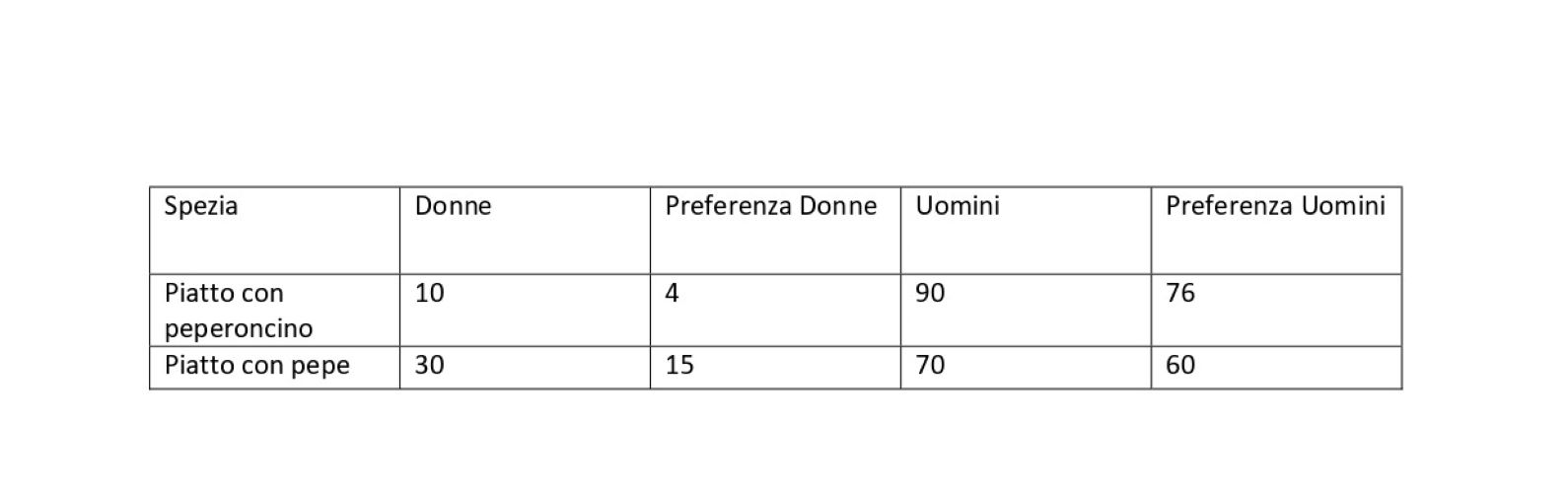
Il piatto con peperoncino è preferito dal 40% delle donne e dal 84,4% degli uomini, mentre il piatto con pepe dal 50% delle donne e dal 85,7% degli uomini. La suddivisione del campione in base al sesso sembra ribaltare il risultato. È il paradosso di Simpson. Le conclusioni sono opposte se consideriamo l’intero campione oppure lo suddividiamo in base al sesso. Perché questo? Le preferenze dipendono dal sesso ed i gruppi sono formati da proporzioni diverse di uomini e di donne. L’introduzione della variabile sesso ha sovvertito i risultati.
Quale conclusione è giusta? Dipende da quello che stiamo cercando. Da un set di dati siamo noi a decidere quale aspetto mettere in evidenza e come. Consideriamo l’efficacia dei vaccini. Dai dati dell’Istituto superiore di sanità si osserva che nella fascia over 80 il numero di ospedalizzazioni (in un arco di 30 giorni) fra vaccinati con ciclo completo è di 1207 unità e di 714 fra i non vaccinati. Tuttavia se consideriamo che in questa fascia il tasso di vaccinazione supera il 90% , otteniamo che il tasso di ospedalizzazione per i non-vaccinati è di circa 9 volte superiore a quello dei vaccinati. Questo è il tipico caso di paradosso di Simpson e delle sue conseguenze. Come scrive Darrell Huff nel 1954 “Se torturi i dati abbastanza, alla fine confesseranno quello che vuoi”.




















“Se torturi i dati abbastanza, alla fine confesseranno quello che vuoi” vedi i risultati delle elezioni: nessuno ha perso e tutti hanno guadagnato.
È il rischio che si corre, a maggior ragione, in un periodo storico in cui siamo sommersi costantemente da montagne di dati.