In questi giorni si susseguono i dati sulle morti per Covid-19 in quasi tutti i paesi del mondo. Gabriele Carelli si è chiesto se, usano la cosiddetta Legge di Benford, fosse possibile trarre qualche conclusione sull’autenticità dei dati riportati. Ecco cosa ha trovato. [Articolo originariamente apparso su Medium e qui riproposto per iniziativa dell’autore].

Sono mesi che si discute su quanto possano essere affidabili i dati sulla diffusione del COVID-19 nel mondo. Una delle domande che mi sono posto più spesso è:

ci sono nazioni che, per “interesse nazionale” (qualsiasi cosa questo voglia dire), tendono a modificare i dati che diffondono al pubblico sui morti da COVID-19 all’interno dei propri confini?

Ho l’impressione che l’opinione comune sia che “si, alcuni stati mentono ai propri cittadini ed al mondo”. Ma per quale motivo? Potrebbe essere per non ingenerare panico, o forse per cercare una (fittizia) conferma nelle proprie politiche di contrasto, o forse per bieche campagne ideologiche, o chissà per quali altri oscuri motivi di real politik… Le opinioni differiscono invece sulla direzionalità che si applica a tali falsificazioni: qualcuno mente per “aumentare” il reale impatto da COVID-19 mentre altri mentono per “diminuire” questo impatto. Ma sarà vero?

È ovvio che non è una domanda alla quale si possa rispondere facilmente, sopratutto per un comune cittadino come me che analizza la situazione dal salotto di casa e non ha accesso a nessuna fonte privilegiata.

Nonostante ciò, ho provato a mettere insieme un po’ di dati pubblici per vedere se se ne potesse tirare fuori qualcosa di interessante. Per fare questo ho utilizzato i dati ufficiali della World Health Organization (WHO). In particolare, nei grafici che seguono, ho utilizzato i dati aggiornati al 19 ottobre 2020.

Ho quindi analizzato la distribuzione del numero di morti per ogni giorno, dall’inizio della pandemia, in ciascuno dei 237 stati presenti nella tabella del WHO. Su tali numeri ho voluto fare un confronto con quanto previsto dalla Legge di Benford.

***

Non ho modo di dare, in questa breve nota, una spiegazione tecnica di cosa sia la legge di Benford e rimando quindi alla pagina wikipedia per una descrizione più approfondita. Basti dire che tale legge

is an observation about the frequency distribution of leading digits in many real-life sets of numerical data. The law states that in many naturally occurring collections of numbers, the leading digit is likely to be small. For example, in sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. If the digits were distributed uniformly, they would each occur about 11.1% of the time. Benford’s law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on

E’ una legge quasi magica che si applica ad insieme vari ed eterogenei di dati come:

• lunghezza di fiumi
• popolazioni di città
• costanti fisiche
• numeri di Fibonacci
• numero di note a piè di pagina sui libri
• ecc…

Condizioni necessarie, ma non sufficienti, affinché un insieme di dati segua la legge di Benford è che:

• ogni campione sia indipendente dagli altri
• sia sufficientemente vario da abbracciare diversi ordini di grandezza (ad esempio la lunghezza dei fiumi che può essere di centinaia o migliaia di metri, decine ma anche centinaia o migliaia di kilometri)
• non siano imposti limiti inferiori o superiori ai dati considerati (ad esempio la popolazione di paesi sotto i 1000 abitanti con molta probabilità non seguirà tale legge)
• non sia composto da numeri identificativi costruiti su strutture “artificiali” (ad esempio i numeri di telefono o coordinate bancarie non seguono tale legge)

Ovviamente ci sono dei limiti a tale legge che non può essere applicata a qualsiasi insieme di dati, pensate solo all’altezza in centimetri/metri della popolazione in cui la prima cifra sarà un 1 o un 2 per (quasi) tutta la popolazione sopra i 3 anni e quindi sicuramente non si applica tale distribuzione. Ma, eccezioni a parte, negli ultimi 90 anni è stata verificata su insiemi di dati così diversi da essere diventata uno strumento nella cassetta degli attrezzi di specialisti dei campi più disparati.

Gli storici della matematica fanno risalire le prime osservazioni su tale fenomeno all’astronomo Simon Newcomb nel 1881, tanto che da molti è chiamata Legge di Newcomb-Benford, con un articoletto di 2 pagine sull’American Journal of Mathematics intitolato “Note on the Frequency of Use of the Different Digits in Natural Numbers”.

Se non avete mai sentito parlare di questa legge vi consiglio di approfondire prima, su wikipedia o dove preferite, altrimenti quanto segue non è probabilmente di immediata comprensione.

Ho deciso quindi, dicevo, di “testare” la legge di Benford sulla distribuzione del numero di morti per ogni giorno, dall’inizio della pandemia, in ciascuno dei 237 stati presenti nella tabella del WHO.

N.B.: sto assumendo che tale distribuzione debba seguire la Legge di Benford e che valgano quindi specifiche condizioni, sopratutto di indipendenza del numero di morti giorno per giorno. Questo assunto non è assolutamente scontato: non saprei come dimostrarlo (a priori) e potrebbe essere contestato. Ad esempio: il numero di morti di un giorno è statisticamente dipendente dal numero di morti del giorno precedente? Confesso che non lo so… Ecco, tenete sempre presente questa importante, importantissima, ipotesi di base falsificata la quale tutto il discorso verrebbe a cadere.

Premesso questo, per l’analisi in questione non sono quindi interessato ai valori assoluti del numero di morti ma esclusivamente alla prima cifra significativa di ognuno di questi numeri per poi applicare la legge di Benford e vedere quanto scostamento si abbia per i dati di ogni nazione.

Proviamo, prima di tutto, a confrontare la distribuzione teorica di Benford con quella che si è avuta in Italia da inizio pandemia:

Aggiungiamo adesso al confronto anche la curva ottenuta mettendo insieme i dati di tutte e 237 le nazioni analizzate:

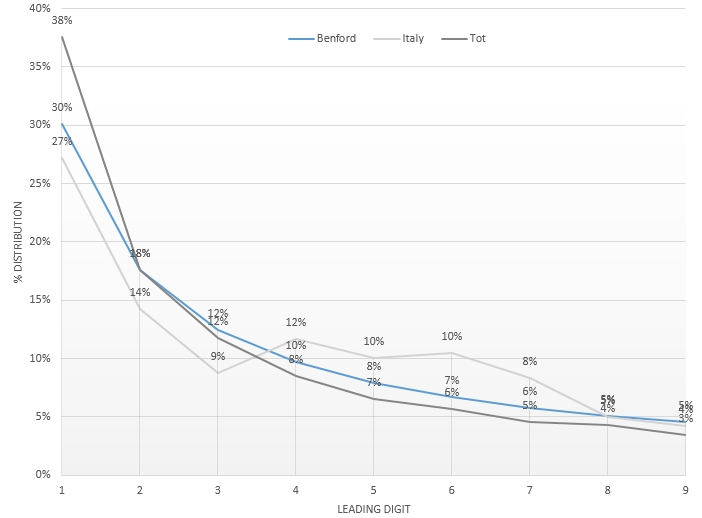
Ovviamente, come ci si doveva attendere, aumentando la dimensione del campione la distribuzione studiata si avvicina maggiormente alla distribuzione teorica. Per il momento, quindi, sembra esserci un generale accordo tra la legge di Benford e la distribuzione del numero di morti per COVID-19 nel mondo.

Ma cosa succede per le singole nazioni?

Discutendo di “analisi statistiche” dobbiamo considerare esclusivamente le Nazioni per le quali si abbiano un numero sufficiente di giornate con almeno un morto. Ho quindi deciso di considerare solo le nazioni che abbiano almeno 200 giorni con almeno un morto nei propri confini. Con questa selezione il numero di nazioni analizzate passa da 237 a 32. Ovviamente, se si prova a rappresentare in un unico grafico le distribuzioni per tutti e 32 i paesi considerati si ottiene un caos di difficile interpretazione anche se si intravede, con qualche eccezione comunque significativa, un andamento medio simil-Benford:

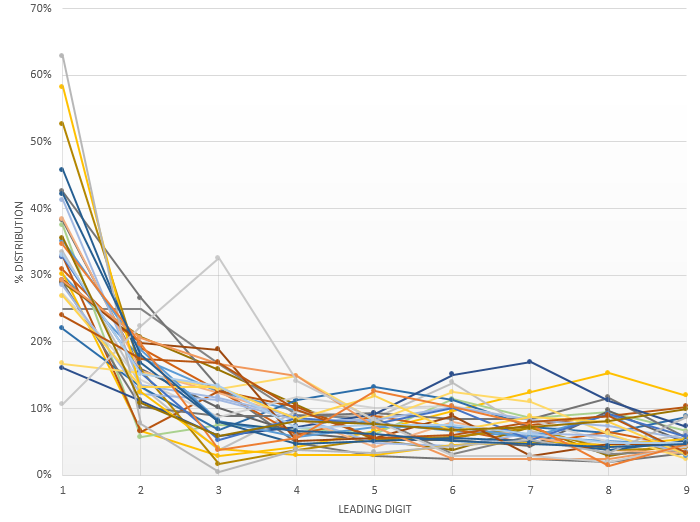
Ma quali sono le nazioni che più si avvicinano e quali invece quelle che più si discostano dall’andamento teorico? Per rispondere a questa domanda non possiamo ovviamente affidarci ad una osservazione qualitativa ma dobbiamo appoggiarci a qualche dato quantitativo. Ho quindi deciso di calcolare, per ogni nazione, lo scarto quadratico medio (Root Mean Square Error — RMSE) rispetto alla distribuzione prevista dalla legge di Benford. Di seguito la tabella con i valori ottenuti per le 32 nazioni prese in esame:

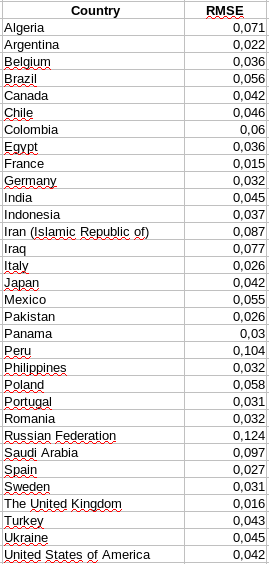
(come dite? manca la Cina nella tabella? Mi sono stupito anche io ma secondo i dati ufficiali la Cina ha avuto “solo” 144 giorni con almeno un morto per un totale di meno di 5.000 morti fino ad oggi. Chi lo avrebbe mai detto?)

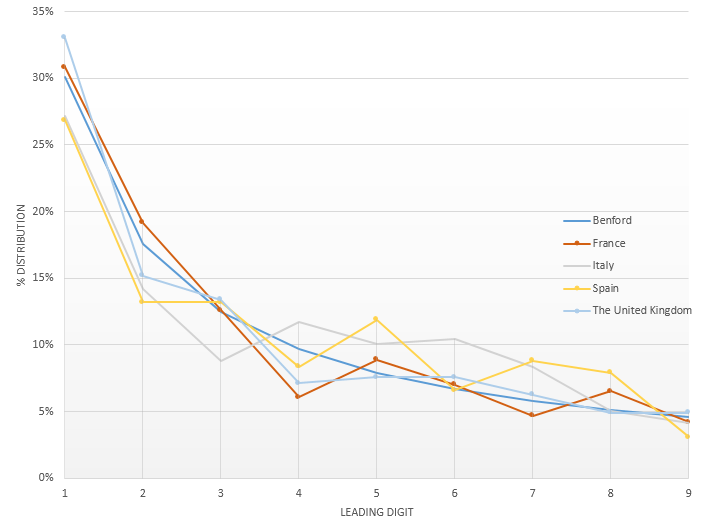
Dalla tabella si vedono, almeno a mio parere, dei valori interessanti: per stati come la Francia, UK, Spagna o Italia l’errore calcolato è basso (non in assoluto ma rispetto alle altre nazioni) e quindi l’accordo con la distribuzione di Benford è maggiore:

mentre i valori più alti di RMSE sono per nazioni come la Russia, il Perù, l’Arabia Saudita o l’Iran; per queste nazioni, quindi, lo scostamento dalla distribuzione di Benford è più marcata:

Non bisogna essere certo esperti di geopolitica per vedere una differenza tra i governi di Francia/Italia/Spagna/UK, da una parte, e Iran/Russia/Arabia Saudita dall’altra (confesso che personalmente non saprei invece inquadrare, dal punto di vista geopolitico, il Perù).

Notata la differenza, ho deciso di mettere a confronto l’RMSE delle 32 nazioni considerate con la loro posizione all’interno del Democracy Index, classifica stilata dall’Economist Intelligence Unit che intende misurare lo stato della democrazia nei vari paesi del mondo. Gli ultimi dati disponibili sono relativi al 2019 ed ordinano 167 paesi dal più “democratico” (rank #1, la Norvegia) al meno democratico (rank #167 Corea del Nord).

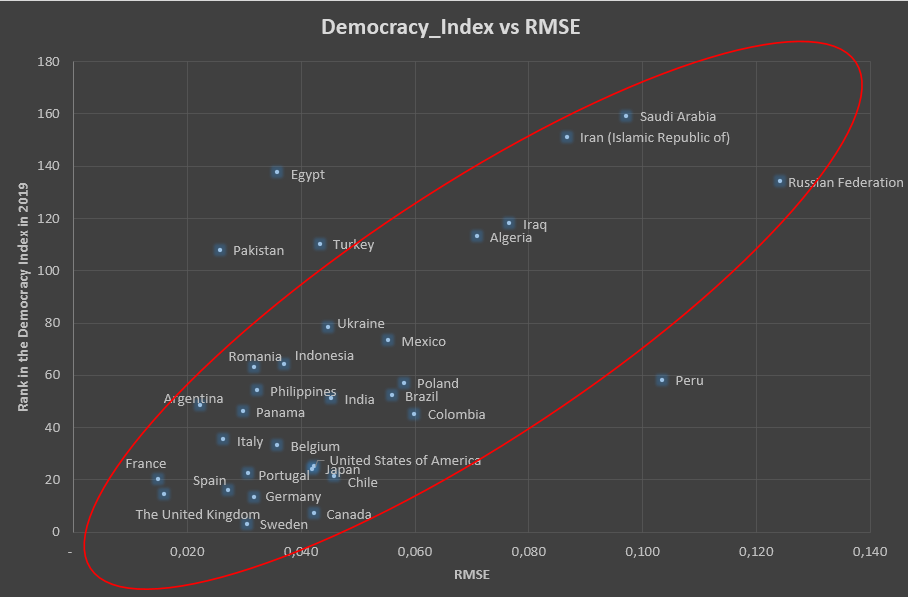
Tolte alcune, comunque importanti, eccezioni (Pakistan, Egitto, e Turchia in un verso e Perù nel verso opposto) si può notare un andamento coerente: all’aumentare del rank nel Democracy Index corrisponde uno scostamento più accentuato dalla distribuzione di Benford. In altre parole: le nazioni indicate nel 2019 come più democratiche (rank basso) presentano dati per il COVID-19 che si avvicinano ad una distribuzione teorica (RMSE basso) e, quindi, pare difficile che siano stati manipolati.

Al contrario, le nazioni che presentano dati per il COVID-19 che si discostano maggiormente dall’andamento teorico (RMSE alto) sono anche quelle indicate come meno democratiche (rank alto) e sono quindi più “sospette” di manipolazione…

Sono stati realmente manipolati? Non è possibile dirlo ma, alla luce dei dati oggettivi, penso che non ci sarebbe da stupirsi.

Nel caso in cui i dati siano stati manipolati, lo sono stati per far “aumentare” artificiosamente il numero di morti o per farli “diminuire” artificiosamente? Questo, purtroppo, è impossibile a dirsi.