In uno studio finanziato dall’Associazione Italia per la Ricerca sul Cancro (AIRC), una collaborazione fra matematici, biologi e medici di istituti universitari, clinici e di ricerca di Milano ha portato allo sviluppo di uno strumento matematico per personalizzare la cura di un tumore celebrale molto aggressivo, il glioblastoma multiforme (GBM).
L’incidenza del GBM in Europa e Nord America è di 3-5 ogni 100.000 adulti ogni anno. Questo tumore colpisce per la maggioranza fra i 60 e gli 80 anni, ma può verificarsi a qualsiasi età. Nonostante tutte le terapie attualmente disponibili, il tempo complessivo di sopravvivenza globale dopo la diagnosi è di soli 15 mesi.
“Malgrado lo sviluppo di nuove tecniche chirurgiche, radioterapiche e farmacologiche” – commenta il dott. Francesco Acerbi, neurochirurgo dell’Istituto Neurologico Besta di Milano – “negli ultimi cinquant’anni il tempo di sopravvivenza per un paziente affetto da GBM non si è modificato in maniera soddisfacente, in ragione della imprevedibilità sulla estensione e sulla progressione della neoplasia. Ci siamo allora chiesti come avremmo potuto meglio sfruttare a livello clinico i grandi passi in avanti fatti dalle tecniche neurochirurgiche e la maggior precisione dalle indagini neuroradiologiche a beneficio del singolo paziente. La matematica ci è venuta in aiuto.”
“La matematica non può curare il cancro” – commenta il prof. Pasquale Ciarletta, docente di fisica matematica al Politecnico di Milano- “ma può senza dubbio aiutare il medico a personalizzare le cure cliniche e migliorare la qualità di vita di ogni paziente. Oggi abbiamo a disposizione degli strumenti tecnologici talmente sviluppati da poter cambiare il classico paradigma che prevede una sola cura per ogni tipo di patologia con quello di dare una cura diversa e personalizzata per ogni paziente affetto dalla stessa patologia. In questo studio clinico noi usiamo la matematica per ricreare il cervello virtuale di ogni paziente dai dati clinici fornitici dalle indagini di neuro-radiologia, come la risonanza magnetica. Abbiamo quindi sviluppato un modello matematico per simulare l’evoluzione della malattia, la rimozione chirurgica ed il trattamento terapeutico, imparando dai dati di follow-up clinico per aggiornare e migliorare continuamente la capacità predittiva del modello proposto rispetto ai dati clinici. In questo modo, il modello matematico diventa una palestra virtuale per il clinico per migliorare l’evoluzione clinica del GBM nel cervello virtuale di ogni paziente.”
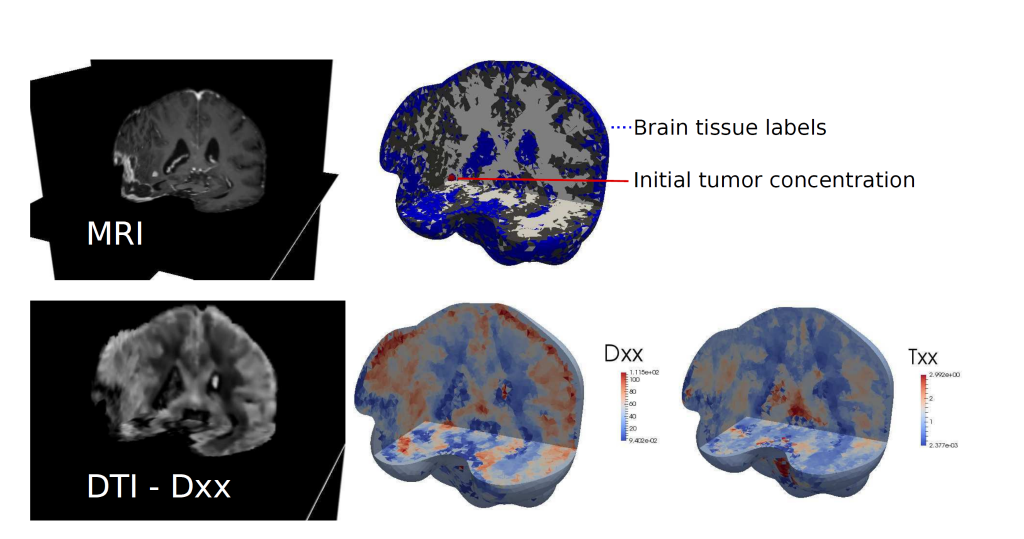
Dati neuroradiologici di paziente affetto da glioblastoma (sinistra) e corrispondente ricostruzione del cervello virtuale (a destra) con integrazione dei dati microstrutturali da Diffusion Tensor Imaging (DTI) e Risonanza Magnetica (MRI). Credit: P. Ciarletta, Politencico di Milano
“Quello che non possiamo investigare in maniera invasiva sul singolo paziente” – aggiunge il prof. Giorgio Scita dell’Università di Milano, group leader all’istituto IFOM di oncologia molecolare – “lo abbiamo studiato su sistemi biologici ex-vivo o in-vitro fatti da linee cellulari di GBM. Ad esempio, abbiamo studiato i meccanismi attraverso i quali una cellula di GBM percepisce il mondo esterno e ne traduce i segnali, in risposta ai quali modifica il proprio comportamento, soprattutto quello migratorio, in isolamento od in gruppo, ed abbiamo integrato queste peculiari caratteristiche nel modello matematico. Ancora molto, però, rimane da comprendere su come avviene la diffusione del GBM nel cervello, su cosa si fonda la plasticità con cui le cellule tumorali si adattano al microambinte, e come identificare nuovi bersagli terapeutici tra i determinanti della capacità migratoria per bloccare l’invasione tumorale.”
“Il reclutamento dei pazienti di questo studio clinico condotto all’Istituto Neurologico Besta si è concluso da pochi mesi” – continua il dott. Acerbi- “ed i risultati preliminari che abbiamo ottenuto sono molto incoraggianti. La capacità predittiva del modello matematico è risultata molto più alta di quella presente in letteratura medica. La possibilità di allargare la base dei dati clinici con più pazienti, anche da altri centri, avrà un’ulteriore effetto migliorativo sull’accuratezza del modello. Non ci sarà bisogno di formare un medico matematico, ma la matematica ci aiuterà nella pratica clinica fornendoci uno software al quale il neuro-radiologo fornirà in ingresso i risultati delle risonanze magnetiche del paziente, per ottenere in uscita una simulazione virtuale dell’evoluzione della patologia. Il nostro obiettivo è quello di permettere al chirurgo di simulare diversi approcci di intervento per ridurre la probabilità di recidive in aree che comprometterebbero la qualità di vita del paziente, e far sì che il neuro-oncologo ed il radioterapista possano ottimizzare tempi e modalità delle cure da somministrare per massimizzare l’efficacia della terapia adiuvante”.
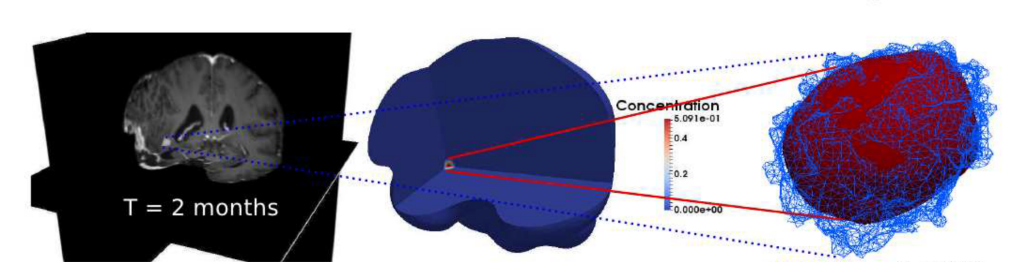
Risonanza magnetica di un paziente affetto da GBM (sinistra); ricostruzione del cervello virtuale (centro) e risultato della simulazione del modello matematico per l’evoluzione della lesione, in rosso, rispetto all’estensione clinica del tumore, in blu (destra). Credit: P. Ciarletta, Politencico di Milano.
“Questa collaborazione multidisciplinare” – conclude il prof. Ciarletta – “ci insegna come la matematica possa contribuire ad operare la nuova rivoluzione scientifica verso la medicina personalizzata. I nuovi ed interessanti problemi che ci vengono posti dalla medicina e dalla biologia ci impegnano non solo a livello astratto nella costruzione di linguaggi e strumenti matematici adeguati, ma ci forniscono anche la possibilità di ottenere ricadute concrete sulla salute ed il benessere delle persone.”
Riferimenti bibliografici
Acerbi, F, Agosti, A, Falco, J, Marchesi, S, Vetrano, IG, DiMeco, F, Bizzi, A, Ferroli, P, Scita, G, Ciarletta, P, ”Mechano-biological features in the Patient-Specific Treatment of Glioblastoma”, Neuromethods, Springer, 265-287, (2021)
Agosti, A, Ciarletta, P, Garcke, H., Hinze M., “Learning patient-specific parameters for a diffuse interface glioblastoma model from neuroimaging data”, Mathematical Methods in the Applied Sciences 43 (15), 8945-8979.(2020)
Agosti, A, Marchesi, S, Scita, G, Ciarletta, P, ”Modelling cancer cell budding in-vitro as a self-organised, non-equilibrium growth process”, Journal of Theoretical Biology, 110202, (2020).
Pozzi,G, Marchesi, S, Scita, G, Ambrosi, A, Ciarletta, P, ”Mechano-Biological Model Of Glioblastoma Cells In Response To Osmotic Stress”. Mathematical Biosciences And Engineering 16(4): 2795–2810, (2019).
Agosti, A, Antonietti, PF, Ciarletta, P, Grasselli, M, Verani, M, ”A Cahn-Hilliard–Type Equation With Application To Tumor Growth Dynamics”, Mathematical Methods In Applied Science, 40, 7598–762, (2017).























